基于时频分布的电子侦察信道参数估计方法

江 莉,董 惠,李 林,刘 利

(1.西安建筑科技大学信息与控制工程学院,陕西西安 710055;2.西安电子科技大学电子工程学院,陕西西安 710071)

0 引言

在通信、雷达、声纳等电子侦察与对抗方面,截获的信号总是伴随着多径干扰。通过ESM、ELINT等电子侦察设备截获的信号,对信道参数进行有效的估计,可以提高信号检测概率,提高信号参数估计精度,在电子侦察与对抗方面具有非常重要的应用价值。多径信道参数估计实际上是一个盲反卷积过程,文献[1～2]针对重叠的雷达多径信号,通过天线阵列模型进行多径参数估计,此时需要满足天线阵列数大于多径信道个数的条件。对于单通道侦察接收设备而言,仅有一个观测脉冲序列,信道一般具有时变性,因此理论上单个多径信号的盲反卷积的解是不存在的。文献[3]针对多径信道中的信号调制识别问题,采用子空间方法估计信道参数,该方法对噪声敏感,适用范围有限。文献[4]采用循环自相关方法通过构造降阶函数对多径信号进行检测与参数估计,但该方法仅适用于LFM信号。本文针对单通道电子侦察系统,提出了一种基于时频分布的信道参数盲估计方法。该方法快速简单,参数估计准确,分辨率高。

1 理论基础

1.1 信道模型

假设发射信号为s(t),经过多径信道传输,最后接收到的信号可表示为:

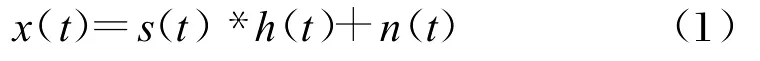
式中,h(t)为传播信道的冲激响应,n(t)为窄带高斯白噪声。

因为各径时延和幅度因子均未知,即使不考虑噪声,数学上(1)式的解不唯一。假设源信号s(t)为:

式中,a(t)和φ(t)分别是瞬时幅度和相位。

由多径信道模型可知,每一多径信号分量与源信号s(t)具有相同的瞬时频率结构,其差别仅在于时间延迟。因此,可通过时频域的匹配滤波完成多径参数估计。通过Moyal公式[5],可以将任意的时频互分布形式与其时域信号相联系,

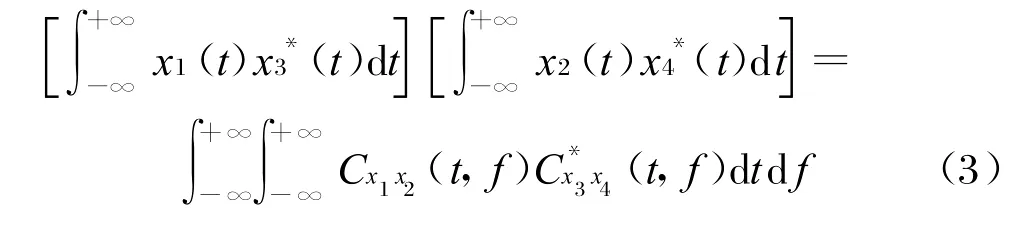
令x(t)=x1(t)=x2(t),s(t-τ)=x3(t)=x4(t),可得:

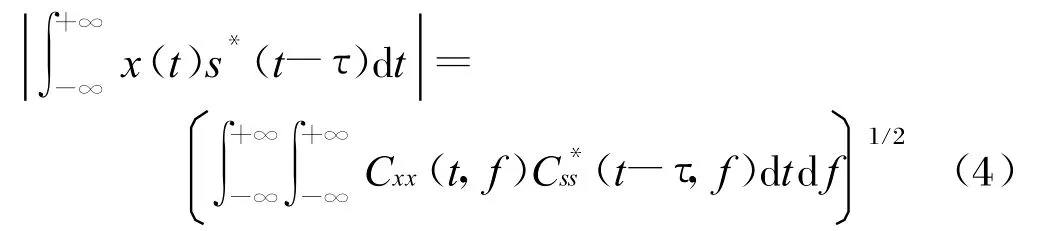
因此,时域匹配滤波同样可以在时频域进行。

1.2 时频分布

短时傅里叶变换是最基本的线性时频表示方法,可定义为:

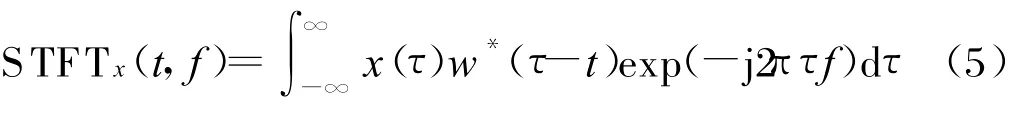
式中,w(t)是窗函数。根据不确定原理,时间窗宽度和频率窗的宽度彼此成反比。若时间窗取得较长,则可得到较好的频率位置,但是时间分辨率却比较差。因此,好的时间分辨率必然意味着差的频率分辨率。相反地,好的频率分辨率意味着差的时间分辨率[6]。

具有双线性特性的时频分布(称为Cohen类)可以用统一的形式表示为:

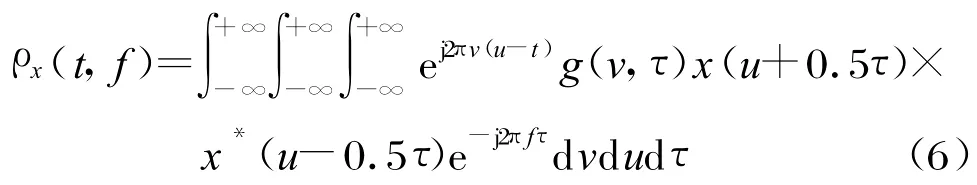
式中,g(v,τ)是加权函数,称为核函数。特别地,当g(v,τ)=1,即ψ(t,ω)=2πδ(t)δ(ω),可得常用的Wigner-Ville分布。WVD具有很多优良的性质,在所有的时频技术中具有几乎最优的时频分辨率,但是其主要缺点是会产生交叉项干扰。

时频分布与模糊函数密切相关,模糊函数A(v,τ)可定义为[7]:

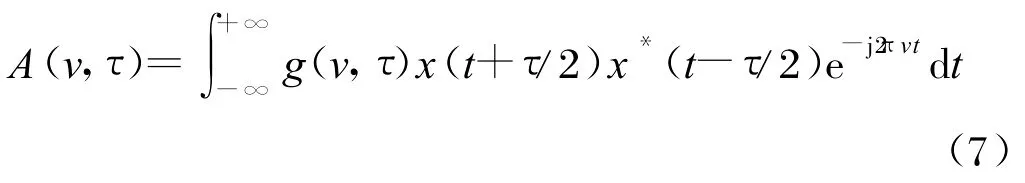
对传统的模糊函数用核函数进行平滑,然后再进行二维傅里叶变换,即可得到Cohen类二次时频分布的统一形式。一个信号的Cohen类时频分布实际上是一个时频域上的二维函数对该信号WVD平滑的结果,通过适当的核函数选择,可以减小或去除多分量信号的交叉项干扰,但交叉项的抑制会导致时频分辨率下降。

2 基于时频分布的多径信道估计

2.1 多分量信号的时频分布

多径信号也可看作一类特殊的多分量信号。为了有效地在时频域进行匹配滤波,首先对WVD的自身项和交叉项在时频平面的分布特点进行研究。简单起见,假设分析信号x(t)包含两个信号分量s1(t)和s2(t)。

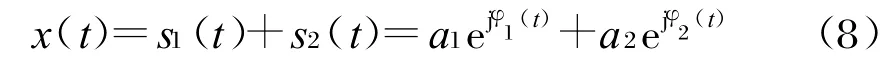
式中,φ1(t)和φ2(t)分别表示两信号分量的瞬时相位。根据WVD的定义有:

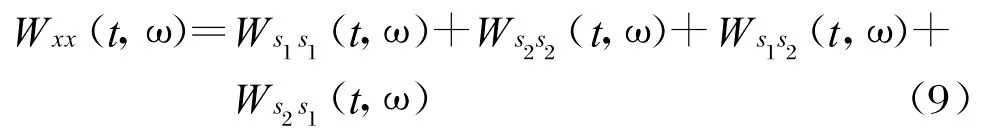
式中,前两项为自身项,而后两项是交叉项。交叉项由不同信号分量之间的相互作用造成,严重影响了信号时频分布的分辨性能和解释性。

对于式(9)的自身项Ws1s1(t,ω),将φ1(t)在t附近按照Tay lor级数展开可以得到:

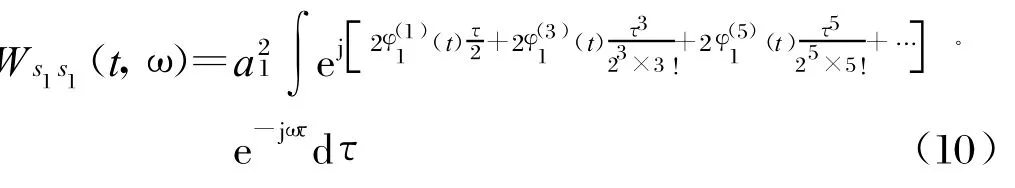
同理,交叉项Ws1s2(t,ω),将φ1(t)和φ2(t)分别按照Tay lor级数展开可以得到:

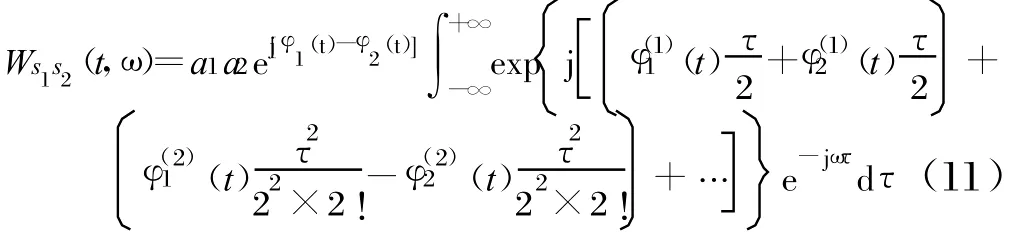
式(10)和式(11)中的Fourier变换求解较为复杂,这里仅做定性分析。以式(10)为例,其中的时域函数的导数可表示为:

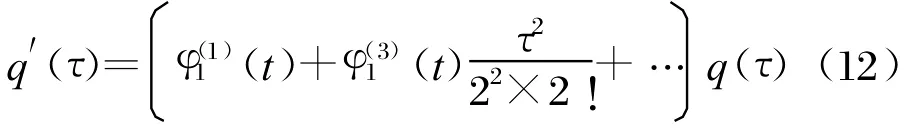
根据Fourier变换的时域和频域微分的性质,可得:

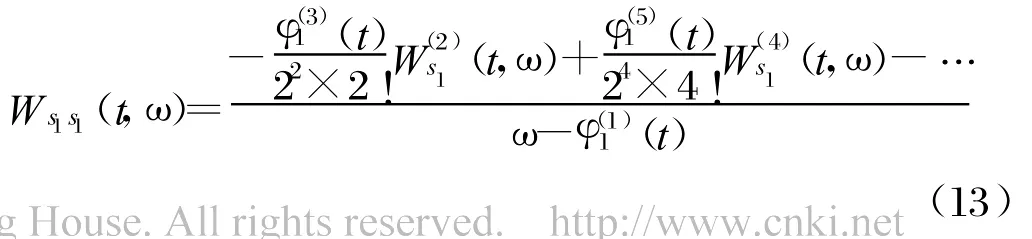
上式是一个高阶齐次微分方程,其通解为一实函数。且Ws1 s1(t,ω)会在瞬时频率ω=φ(11)(t)处出现峰值。同时由于相位中高次项的作用,会产生由信号自身带来的交叉项。同理,式(11)中信号交叉项的WVD也可表示为一个高阶齐次微分方程的解:

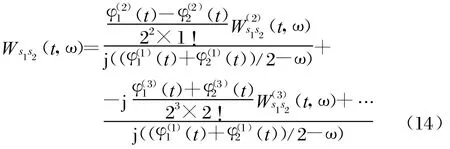
可以看出,信号交叉项的WVD一般为复函数,其模值在ω=(φ′1(t)+φ′2(t))/2时具有峰值,同时由于相位中高次项的作用,会产生复杂的交叉项干扰。

特别地,如果信号相位的三阶以上的导数为零,即LFM信号,则:

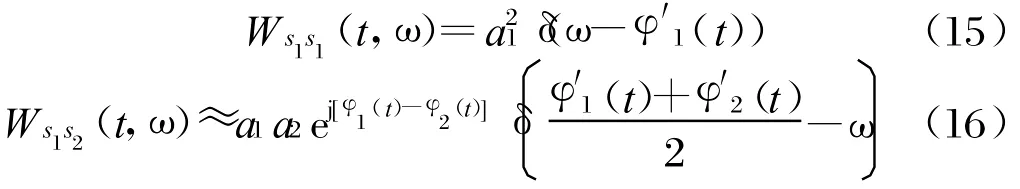
此时,自身项就是位于该信号瞬时频率位置上的一个冲激函数,表现出最佳的时频聚集性。而两个信号的交叉项在两信号瞬时频率的中心位置处出现冲激,在其他区域也有交叉项产生,并且离中心频率越近,交叉项干扰越大。实际中,由于信号分量间能量的差异,交叉项的峰值有可能大于信号自身项。此时,交叉项的幅度随时间振荡,振荡的瞬时频率主要受两信号瞬时相位差影响。

2.2 基于时频分布多径参数估计

通过以上分析可知,相比其他二次时频分布,WVD形式最为简单,具有最优的时频聚集性,但交叉项的干扰不可避免。对于线性调频信号,假设信道冲激响应h(t)=a1δ(t)+a2δ(t-D 2),即仅包含一路多径信号,经推导可得:

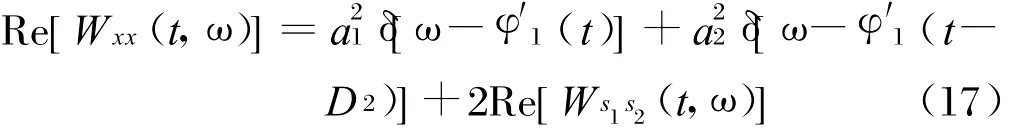
对于离散信号,并根据交叉项时频分布振荡的特点,信道参数可近似表示为:

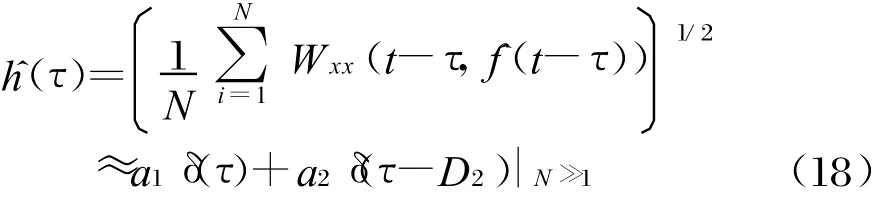
式中,τ=1,2,…,N,N为信号长度。一般源信号s(t)的能量要大于其他多径分量,因此可通过时频图中的峰值轨迹来估计源信号的瞬时频率f(t)。

由交叉项引起的信道估计误差可表示为:

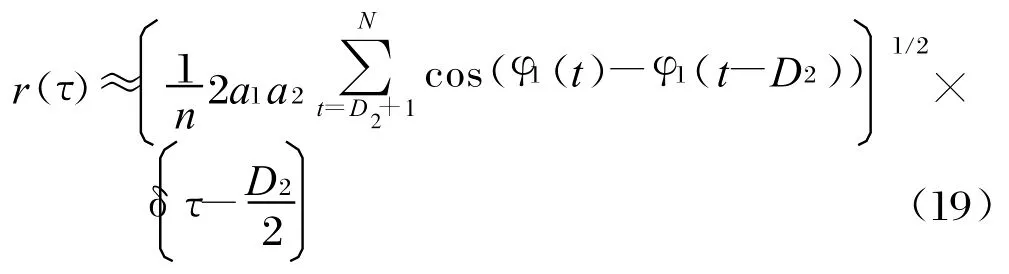
由此可证明,数据长度越长,r(τ)越小,信道参数估计精确越高。另外,信号的调频斜率越大,即相位差(φ1(t)-φ1(t-D2))越大,r(τ)越小。

然而,实际中处理的信号总是长度有限,调制方式复杂,信号的WVD会产生由自身项带来的交叉项干扰,且形式较为复杂。交叉项干扰将会产生错误的信道参数估计。可以采用平滑伪WVD,或其它Cohen类WVD抑制交叉项,但却会大大降低信道参数估计的分辨率和精度。基于此,本文将短时傅里叶变换与WVD相结合,利用短时傅里叶变换良好的抑制交叉项性能,对WVD时频图进行滤波。在抑制交叉项干扰的同时,有效保留时频图的高分辨性能。算法流程如图1所示。

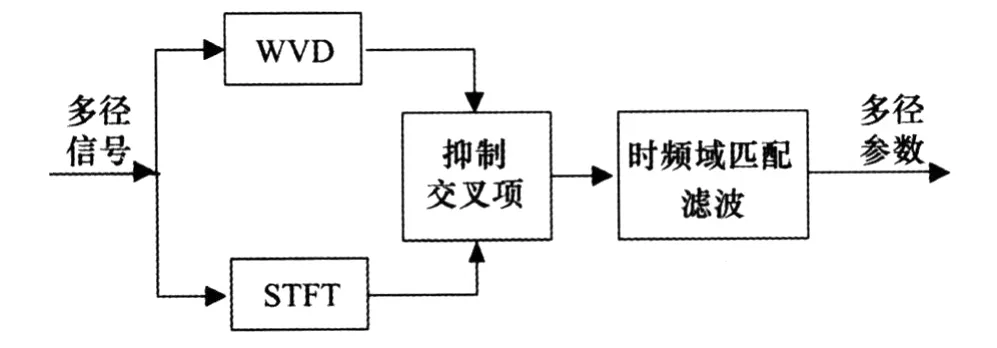
图1 基于时频分布的多径信号参数估计

3 仿真实验与结果分析

计算机仿真的多径信号包含1个源信号和2个多径分量。信道参数为:多径时延D2=300、D3=500,幅度因子a2=0.4、a3=0.3。对于LFM信号,信噪比为5dB,结果如图2所示。

图2(a)是通过对Choi-William s分布[8]进行时频域匹配滤波得到的多径估计结果。可以看出,CWD有效地抑制了交叉项干扰,并在多径时延处出现峰值。然而多径滤波结果的分辨率较低。图2(b)是直接采用WVD进行时频域匹配滤波的结果,可以看出,该方法具有较高的分辨率。然而,由于噪声和各种交叉项干扰影响,以及计算WVD时FFT长度的限制,匹配滤波的结果出现很多虚假的信道参数估计。

与上面两种方法相比,图2(c)是采用本文方法进行时频域匹配,由多径参数估计结果可以看出,该方法有效地抑制了各种干扰因素的影响,保留了对多径幅度因子和时延估计的精度和分辨率。需要注意的是,利用短时傅里叶变换对WVD时频图进行滤波前,先要对短时傅里叶变换结果进行0/1二值化处理。二值化处理时采用的门限不能选择过高,否则会导致多径分量的时频脊线丢失,而门限过低对估计结果的影响并不是很大。实验中选取的归一化后的二值化门限为0.25。

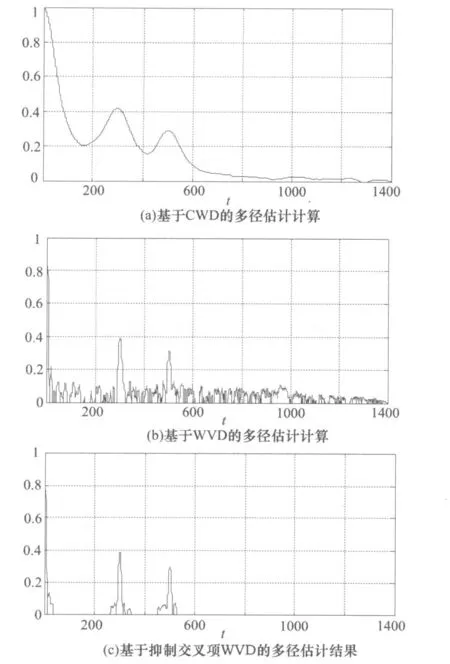
图2 多径LFM信号盲估计

图3是在不同信噪比下,采用本文方法分别对第1多径D2和第2多径时延D3估计的绝对误差。其中,LFM信号参数与上面实验相同。除此之外还增加了4阶频率调制信号,多径参数与LFM信号相同。图中曲线是100次M onte-Carlo实验的平均结果。可以看出,即使在较低信噪比下,采用本文方法对多径LFM和四次频率调制信号的时延估计误差都比较小。当信噪比大于17dB时,时延估计误差基本上可看作零,而此时对幅度因子a2和a3的估计的绝对误差都在0.01以下。且对于多径LFM信号的估计误差要小于四次频率调制信号,这与前面第2节中的分析结果一致。

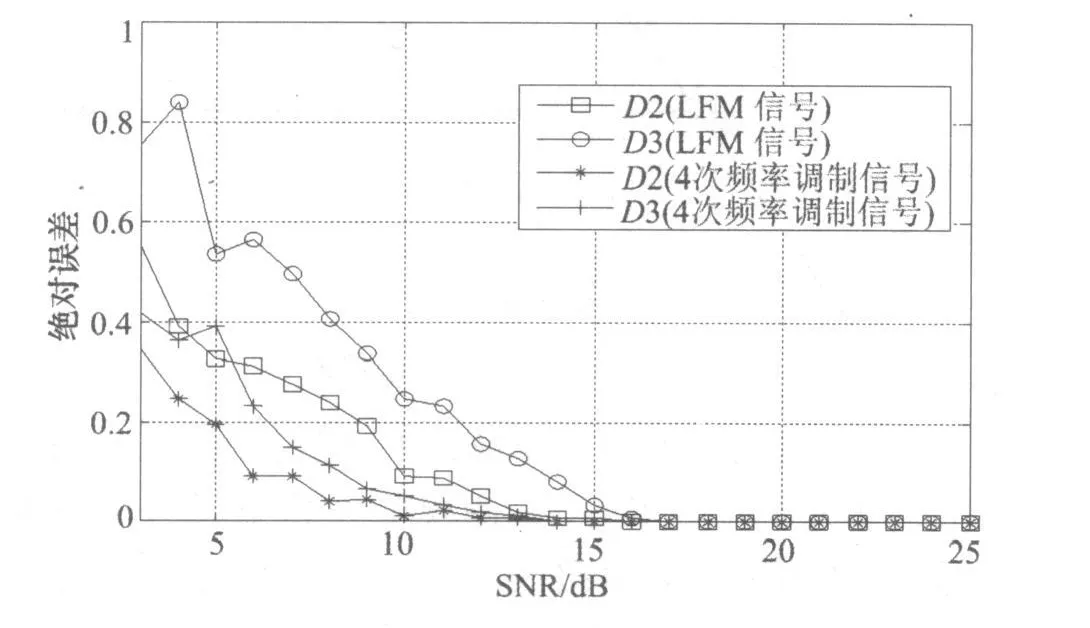
图3 时延的估计性能

4 结束语

理论分析和计算机仿真实验证明,本文提出的方法简单、有效,且估计结果具有较高的分辨性能和估计精度。然而,源信号的瞬时频率估计对算法性能影响较大,在输入信噪比较低的情况下,信道估计性能将会受到较大的影响。另外实际中接收到的信号可能仅是发射信号的一部分,源信号和多径分量信号会产生一定的失配,匹配滤波的性能也会受到较大的影响。此时应该引入其他的瞬时频率估计方法,进一步抑制交叉项干扰。■

[1] Ayadi J,Zhan H,Faserotu J.Maximum likelihood time of arrival estimation for u ltrawideband signals[J].International symposium on Signal Processing and its app lication,2007(2):1-4.

[2] Swind lehurst A L,Gunther JH.Methods for blind equalization and resolution o f overlapping echoes of unknow n shape[J].IEEE Trans.on Signal Processing,1999,47(5):1245-1254.

[3] 王彬,葛临东,徐立清.一种多径信道中的调制识别算法[J].数据采集与处理,2007,22(4):440-446.

[4] 史建峰,王可人.基于循环相关变换的多径LFM信号检测与参数估计[J].电子与信息学报,2007,29(6):1377-1379.

[5] H law asch F.Regularity and unitarity of bilinear time-frequency signal rep resentations[J].IEEE Trans.on Information Theory,1992,38(1):82-94.

[6] Chen VC,H ao L.Time-frequency transforms for radar imaging and signal analysis[M].Boston,London:A rtech H ouse,2002.

[7] Barkat B,Boashash B.A high-resolution quadratic timefrequency distribution formu lticomponent signals analysis[J].IEEE Trans.on Signal Processing,2001,49(10):2232-2239.

[8] Sejdic E,Djurovic I,Jiang J.Time-frequency feature representation using energy concentration:An overview o f recent advances[J].Digital Signal Processing,2009,19(1):153-183.