热控涂层参数对卫星辐射特性的影响

杨 明,郑海燕

(1.解放军电子工程学院安徽省红外与低温等离子体重点实验室,安徽合肥 230037;2.中国人民解放军96634部队,江西南昌 330200;3.安徽淮北工业学校,安徽淮北 235000)

0 引言

卫星观测主要依赖光学探测系统对空间飞行卫星的探测、发现和跟踪。卫星的可见光辐射主要取决于反射的太阳辐射,而红外辐射与其温度紧密相关,由于卫星表面一般都有热控涂层,所以研究卫星辐射特性,必须考虑热控涂层的影响。文献[1～4]分别计算了卫星的温度和红外辐射。从计算结果来看,卫星在空间轨道飞行时,辐射特性不明显。为提高目标探测精度,应当发展卫星的多光谱辐射特性研究。本文分析了卫星红外和可见光辐射的计算方法,研究热控涂层参数改变对在轨飞行卫星表面温度和辐射的影响。

1 热控涂层的温度

热控涂层是专门用于调整固体表面热辐射性质,从而达到对物体温度控制目的的表面材料。航天器在太空飞行时,要将内部产生的热和吸收的空间外热流排散出去,使航天器的温度达到一个合适范围。航天器单位面积辐射散热量大小主要由涂覆在其外表面上的热控涂层的热辐射性质所决定[5]。

在建立航天器表面传热模型时,假设内部发热元件在航天器内表面的辐射照度E为均匀的。采用内节点区域离散法,将卫星表面计算区域划分为多个微元控制体,每个控制体在舱体厚度方向也划分两层。同一控制体内各物性参数均匀,如图1所示。

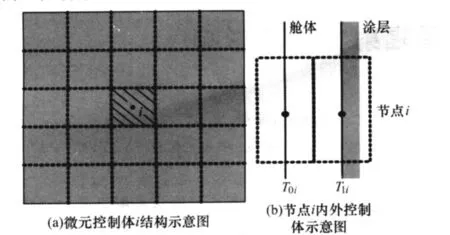
图1 微元控制体示意图

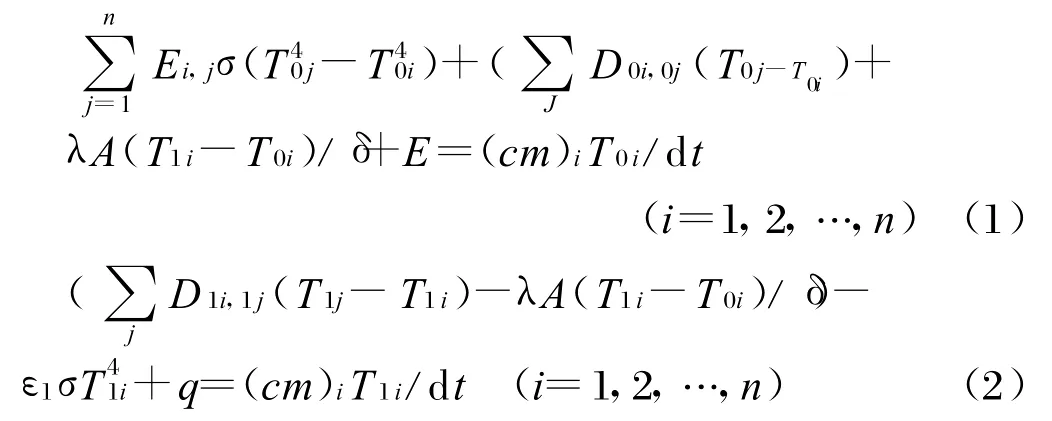
对图1(b)中所示的节点i的内、外两个控制体分别建立节点平衡方程为:式中,T0 i、T1i分别表示节点i的内外控制体温度;Ei,j和D 0i,0j为节点i、j内表面的辐射换热系数和传导系数;λ、δ、c、m分别为卫星舱体表面铝层的导热系数、厚度、比热容、控制体的质量;ε1为涂层发射率;q为节点吸收的外热流密度,该热流由太阳辐射、地球辐射、地球反照辐射组成[6],计算公式为:

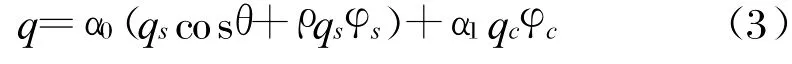
式中,α0、α1分别为热控涂层可见光和红外吸收率,α1=ε1;qs、qe分别为太阳常数和地球红外辐射热流密度,qs=1353W/m2、qe=220W/m2;ρ为地球的太阳反射率;θ为面元的外法线与太阳入射方向的夹角;φs、φe分别为地球反照角系数和地球辐射角系数。

2 卫星辐射特性的计算模型

卫星辐射由自身辐射和反射的太阳辐射、地球辐射和地球反照辐射构成。在确定卫星表面温度分布后,将卫星看成一个朗伯发射体来计算卫星自身辐射,卫星反射辐射则按照漫反射理论计算。卫星表面面元的光谱辐射出射度可以表示为:

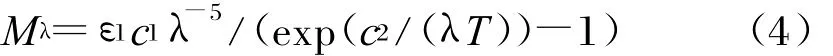
反射可见光谱辐射可表示为:

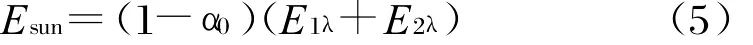
在可见光波段,地球辐射能量近似为0。

反射红外光谱辐射可表示为:

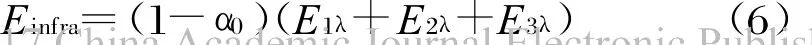
E1λ、E2λ和E3λ分别表示卫星表面的太阳辐射照度、地球反照辐射照度和地球辐射照度。则卫星的可见光辐射出射度Msun和红外辐射出射度Minfra分别为:

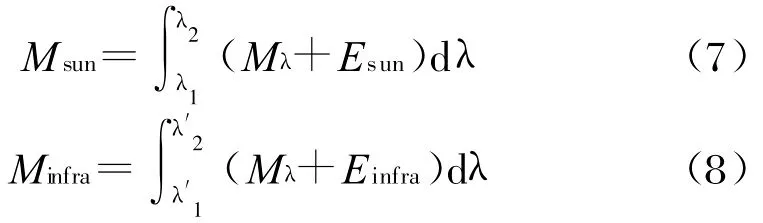
太阳是距离地球最近的恒星,太阳半径rs≈6.96×105km,地球与太阳的平均距离1AU≈1.5×108km。由于日地距离非常远,可认为日地距离是不变的[7],因此由能量守恒定律有:

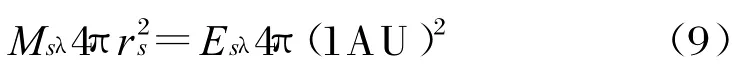
式中,Msλ为太阳光谱辐射出射度;Esλ为太阳在地球大气层外的光谱辐照度。若太阳可等效成温度为5762K的黑体,则由普朗克黑体辐射定律可以得到太阳直接照射卫星上的光谱辐射照度为:

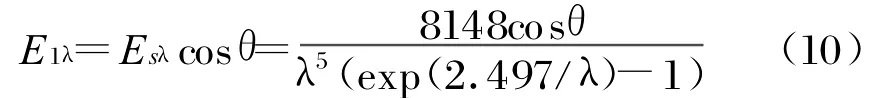
地球等效成温度为293K的黑体[5],它的表面辐射遵守朗伯定律。由黑体辐射定律求得地球表面的光谱辐射出射度为:

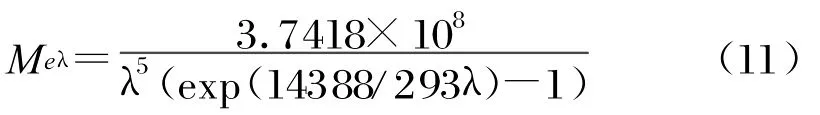
地球辐射在卫星表面的光谱辐照度为:

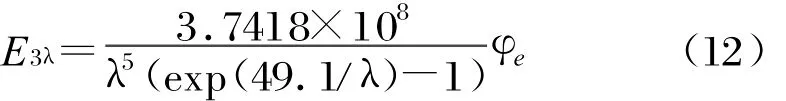
地球对太阳辐射的反射可认为是地表均匀的漫反射,由此在计算地球反射太阳辐射时可将地球当作二次光源来处理。地球对太阳辐射的平均反射率为30%,由此通过同计算地球辐射时同样的方法,可得到地球反射的太阳辐射在卫星上的辐照度为:

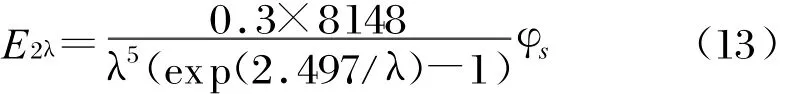
3 计算结果及分析

假定某一圆形轨道、六面体结构的三轴稳定低轨卫星,卫星轨道半径为6653km,轨道倾角iθ=60°,卫星运行周期为5400s。太阳直射地球赤道,初始时刻定为会日点,在第一个周期内卫星进、出地球阴影区的时刻分别为1890s和3510s。卫星各点的初始温度都为300K。以对地面为例,热控涂层的可见光吸收率和红外发射率取表1所列出的三组数据。分别计算不同参数下对地面的可见光和红外辐射。图2表示空间环境(太阳、地球)在卫星对地面上的辐射照度,在地球阴影区只有地球辐射照度,约210W/m2。

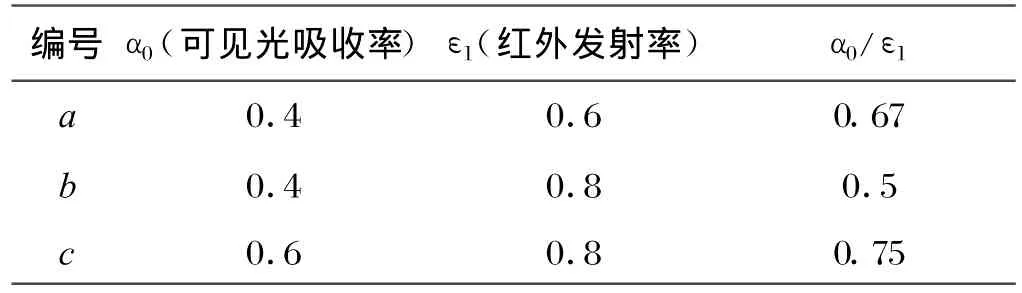
表1 热控涂层参数

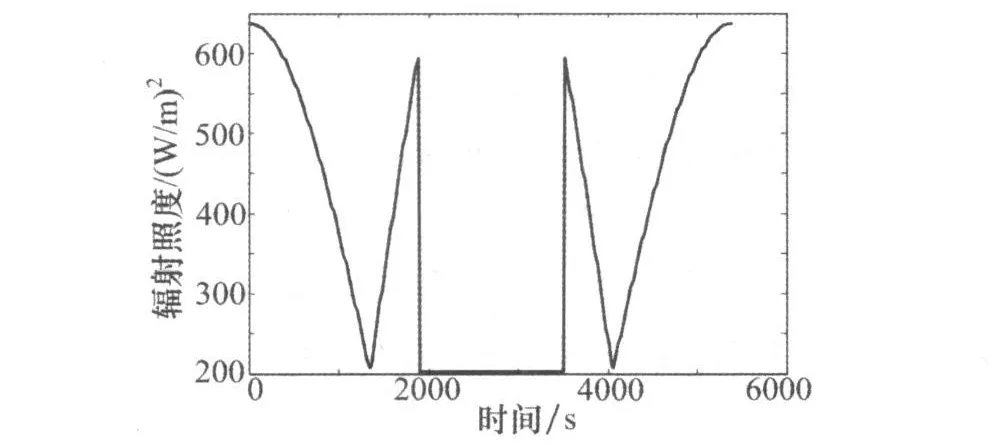
图2 空间环境在卫星对地面上的辐射照度

图3为卫星表面温度变化曲线:(a)列出了从初始时刻起,对地面的温度变化曲线,总体上经过5～7个周期的运行后,温度已成周期性变化;(b)为温度稳定后周期变化曲线,选择了第8个周期,即运行时间为43200～48600s。从图中可以看出温度变化幅度不是很大,基本都在6～8K之间。同时,参数a相对b、c而言,最先达到平衡,且平衡温度也最高,b稍低,c的平衡温度最低。

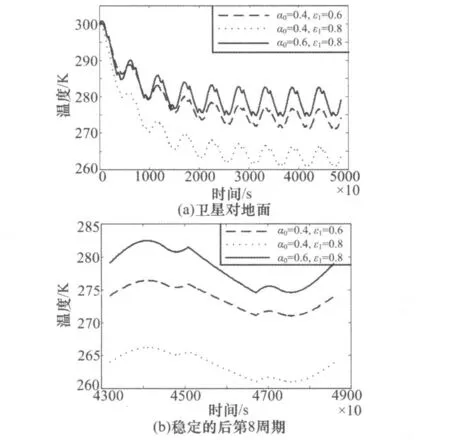
图3 卫星表面温度变化曲线

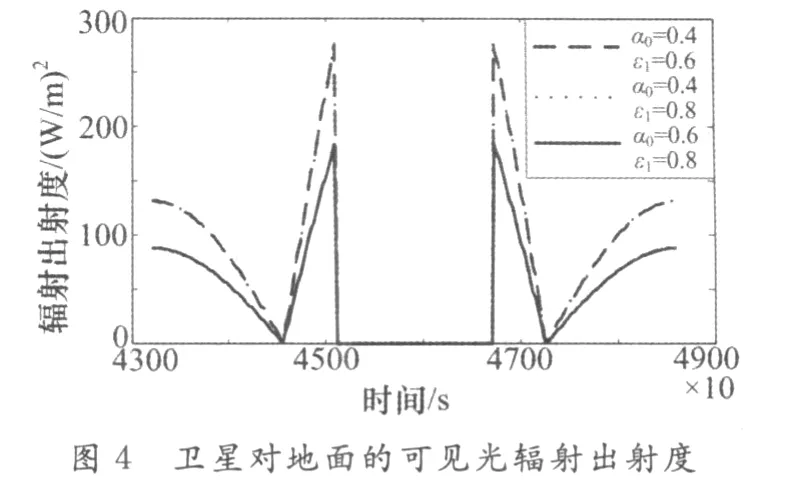
图4列出了卫星温度稳定后对地面的可见光辐射出射度(波段为0.28～0.83μm),参数a的可见光辐射最小,参数b、c基本相同。这是由于卫星的可见光辐射基本上都是反射太阳光辐射,参数a的可见光反射率最小,参数b、c的可见光反射率相等,所以出现图中的结果。在地球阴影区既接收不到太阳直接辐射,也没有地球反照的太阳辐射,所以可见光辐射为0。

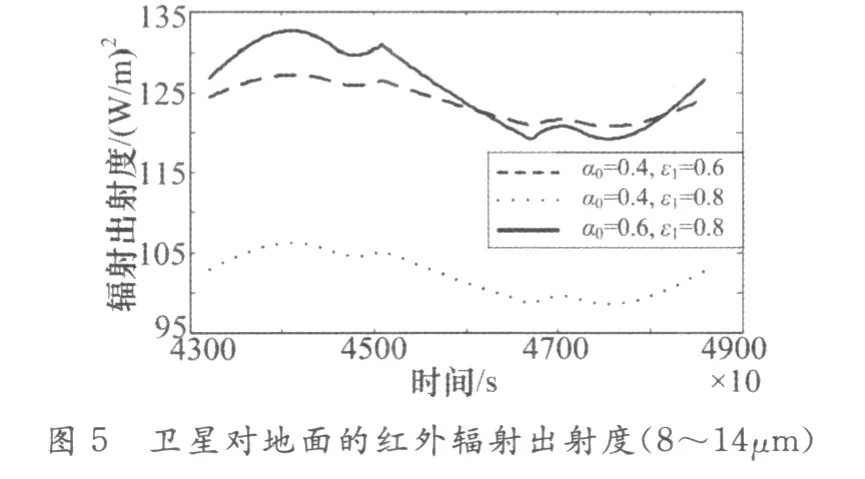
图5为对地面在8～14μm波段的红外辐射出射度,变化趋势基本与温度变化趋势相同,这是由于地球对卫星对地面的角系数在卫星飞行过程中不变,故对地面接收到的地球辐射不变。图示一段时间参数a的红外辐射低于参数b,这是由于该短时间内参数a、b对地面的温度都比较低、自身红外辐射较小,而参数b的红外反射率比参数a高、反射的地球红外辐射较高。

4 结束语

卫星对地面的辐射特性是陆基、海基和空基光电探测的主要探测对象。结合图4、5可以看出,在不同参数条件下,对地面可见光辐射小的红外辐射较大,红外辐射小的可见光较大。所以如何选择合理、优化的热控涂层参数来提高探测和识别的精度,是卫星在热控设计中必须考虑的问题。■

[1] 薛丰廷,汤心溢.空间目标瞬态温度特性研究[J].激光与红外,2008,38(8):223-225.

[2] 孙凤贤,夏新林,刘顺隆.航天器温度场的蒙特卡罗法计算[J].哈尔滨工程大学学报,2001,22(5):10-12.

[3] 韩玉阁,宣益民.卫星的红外辐射特性研究[J].红外与激光工程,2005,34(1):34-37.

[4] 沈国土,杨宝成,蔡继光,等.卫星红外辐射场理论模拟[J].中国空间科学技术,2005,4(2):6-10.

[5] 侯增祺,胡金刚.航天器热控制技术[M].北京:中国科学技术出版社,2007.

[6] 闵桂荣.卫星热控制技术[M].北京:中国宇航出版社,1991.

[7] 舒锐,周彦平,陶坤宇.空间目标红外辐射特性研究[J].光学技术,2006,32(2):196-199.