无人飞行器在线航迹规划技术研究

胡中华,赵 敏

(南京航空航天大学自动化学院,江苏南京 210016)

0 引言

域内完成任务,同时保存自己,达到最佳的作战效果,此即无人飞行器航迹规划[1]。

随着高新技术的发展,现代战争已经呈现出明显的无人化趋势。在未来信息化战争中,无人飞行器将扮演越来越重要的角色。因此,在实时环境中,不仅要求在有限的、尽可能短的时间内为无人飞行器迅速地规划出下一段可飞航迹,而且要求在周围环境发生变化时,无人飞行器能够“感知”到这种变化并迅速根据新的信息重新对路径进行寻优,找出在满足无人飞行器系统机动性能约束条件下,无人飞行器生存概率最大且经济效益最大的参考航迹,使得执行战术任务的无人飞行器能突防战场的威胁环境,并在敌方防空区

1 在线航迹规划问题的描述

根据不同的任务环境,无人机航迹规划可分为静态规划和动态规划。

静态规划是根据先验数据人为给定任务环境,然后把预先规划好的最优路径装载在无人机上,无人机自动驾驶沿预定航线飞行。关于静态规划(离线规划)问题,许多学者作了大量的工作,智能算法方面主要有:A*算法、遗传算法、蚁群算法等等;航迹几何建模方面主要有:通过构建威胁场的Voronoi图,得到回避威胁的航迹段,再用Dijstra法求解最优路径。这种方法的缺点是预先给定的战场环境太过简化,限制了实际可行路线;在无人机规避障碍物研究中,常用栅格法和人工势场法,栅格法速度随着规划空间的复杂度迅速变慢,人工势场法也存在避障缺点[2]。

动态规划(在线规划)即根据环境变化,无人机实时做出反应,重新规划路径[3]。无人机动态航迹规划需要考虑无人机机动性能约束及威胁场约束。在未知环境下,威胁场具有突发特性,主要包括随机风场、地理障碍、雷达、导弹及高炮等威胁源。也就是说,应考虑无人机在飞行过程中能根据位置变化获取传感信息、进行信息融合,并结合预定任务进行动态航迹规划,将规划的结果以指令方式发送给机载自动驾驶仪,从而控制舵机实现按规划的航迹飞行。

2 动力学约束

动力学约束主要包括以下几个方面。

1)最大爬升角 在三维航路规划时必须考虑无人机的最大爬升角。影响最大爬升角的因素主要包括无人机的发动机性能、翼型及翼面、飞行高度及气候状况,通常通过控制水平尾翼及增加推力实现爬升。爬升角不能过大,太大则失去爬升率,有可能导致无人机失速,因此存在最大爬升角,一般飞行状态下,爬升角近似等于俯仰角,如图1所示。因此,爬升角可表示为:

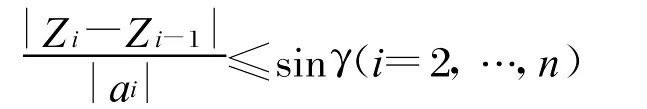
或者

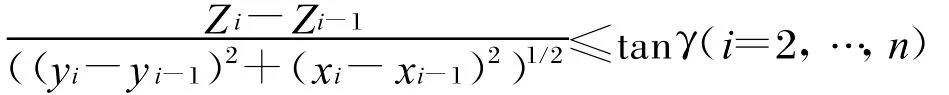
图1 爬升角几何模型

式中,γ表示爬升角,(xi-1,yi-1,zi-1)表示飞机航向尾部点坐标,(xi,yi,zi)表示飞机航向机头坐标。

2)最大航程 无人机在整个飞行过程中的飞行路程,受到飞机燃油和飞行时间配给的限制。设最大航迹长度为L,则每一个航段距离li应满足:

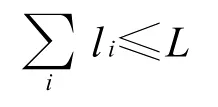
3)无人机的最小飞行高度 设每一段航路飞行高度为Hi,则H i应满足:H i≥H min,(i=1,…,n)。不同于二维航路规划仅考虑水平方向航路规划,三维航路规划必须考虑地形威胁,因此要考虑高度影响。飞行器被敌方探测器发现或被地面防御系统摧毁的概率随高度的增加而增加。而飞得过低往往会使得与地面相撞的坠毁概率增加[4]。因此,要在减少被地面防御系统摧毁的概率和减少坠毁概率之间进行折中。搜索过程中每一个待扩展的节点,只有当它的高度大于或等于给定的最小值H min时,才把它作为可能的航迹点。H m in表示离地面的竖直距离,而非海拔高度。该项指标驱使航迹规划算法去获得低高度的飞行航迹,提高地面掩护效果。

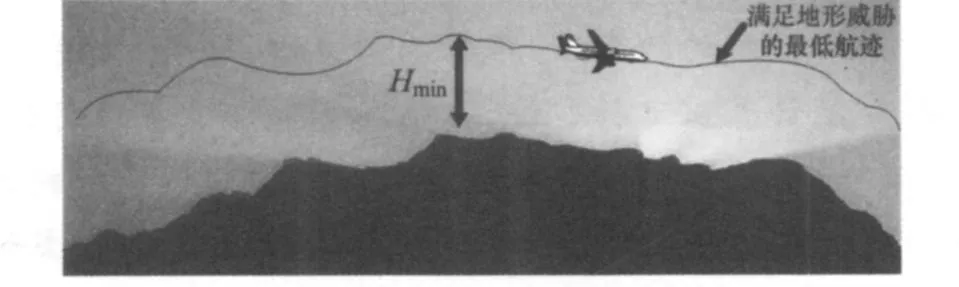
图2 最小威胁曲面示意图

因此,考虑地形威胁的作用,同时结合飞行器的撞地概率,当飞行器以高度H m in离地飞行时,认为其地形威胁最小。因此,在原地形曲面上考虑威胁信息的抬高作用,由所有距离地表高度为Hmin的点构成威胁曲面。飞行在该曲面上的无人飞行器受地形威胁最小,由此得到最小威胁曲面如图2所示。假设地形可以用函数z=f(x,y)表示,则最小威胁曲面为:

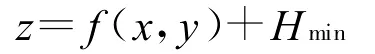
4)最小步长 为无人飞行器在改变飞行姿态前必须直飞的最短距离,即以最低(巡航)速度飞行1s的距离,以RO-9无人机为例,巡航速度130km/h,也就是36m/s,可以简化为40m/s,对于设定范围是400km的作战空间,则可以划分为100格。设最小步长L min,则无人机在改变飞行姿态时必须满足:

图3中,设a为当前航路点,b1、b2、b3、b4、b5为待选的5个航路点,分别对应的步长为L1、L2、L3、L4、L5,其中,仅L1和L4小于最小步长L min,因此,从满足步长程度来选择L2、L3、L5满足最小步长约束,可以作为下一步长的待选节点。

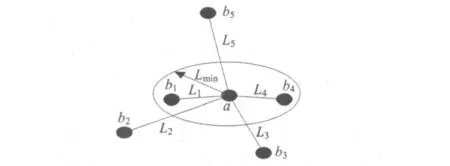
图3 最小步长选择图

5)无人机的最大转弯角度φ 设航迹点(xi,yi)或(xi,yi,zi),设每一航段向量q=(x1-xi-1,y1-yi-1,z1-zi-1),则最大转弯角约束可写:

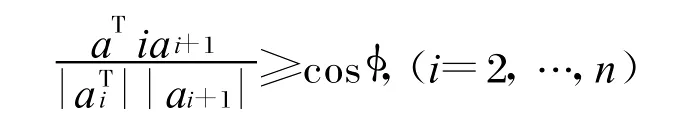
3 威胁场约束

无人机在飞行过程中要考虑威胁源(包括地理障碍、恶劣气候、敌方武器阵地等)的空间位置、威胁源半径、威胁源类型等限制。假设敌方雷达位置坐标(xi,yi),扫描半径ri,i=1,…,m,则区域((a-xi)2+(b-yi)1/2)≤ri为不可飞区,必须绕过这些区域,如图4阴影部分所示。

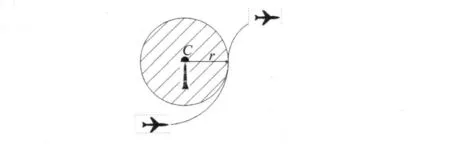
图4 无人机绕过威胁区示意图

具体规划过程中,主要包括:

1)路线搜索:以出发点及可行路线与包络的交点作为搜索起点,攻击路线进入点作为终止点,进行路线的搜索,搜索方法采用深度优先法。

2)威胁场分区:将整个规划区域内的威胁场按相互连接关系进行分组。

3)可行路线识别及网络建立:识别出不同威胁场组间的可行路线,并将所有的可行路线按可能的连接关系构造成路线网络。

4)威胁场包络识别及综合网络建立:识别出规划区域中包含所有威胁场的外边界,并确定可行路线网络、进攻路线及包络的连接关系。

4 在线航迹规划研究现状及算法

近年来,无人机的应用推动了航迹规划的研究。目前美国研制的航迹规划系统已经发展到第三代,正朝着提高效能和降低系统成本等方面继续发展。最有代表性和最著名的航迹规划系统是美国空军的NUH-60A STAR直升机所装备的航迹规划系统。英国已研制成功Pathfinder 2000航迹规划系统。法国目前装备有M IPSY,CINNA和CIRCE2000等系列航迹规划系统。现代无人飞行器航迹规划问题不仅包括航迹预规划,而且需要带有一定的实时性,即在线航迹规划或动态实时航迹规划。

许多学者在离线航迹规划方面作了大量的工作,采用了许多智能搜索算法,如A*算法、遗传算法、蚁群算法等。尽管大量文献已经指出设计开发无人飞行器在线实时航迹规划算法的重要价值,但见之文献的相对于离线航迹规划却少很多,主要研究如下[5-7]:

国内,空军工程大学孙彪采用连续型粒子群优化(PSO)算法进行无人机参考航迹的实时规划,以最大转弯半径、步进、最短距离和回避威胁作为适应度函数的评价指标,得到代表最优航迹的离散点。仿真结果表明该方法收敛时间短,占用内存少,可以满足在线实时航迹规划的要求。丁晓东提出了一种基于RCS的无人机航迹实时规划方法,并采用多阶段分析博弈评估算法对航迹进行优化。仿真结果表明,该方法能够比较好地解决无人机的航迹规划问题。李士波提出了一种基于实时A*搜索的无人机实时航迹规划算法,该算法将飞行器运动与航迹搜索相结合,在飞行器飞行过程中实时规划出下一段航迹;在搜索过程中,使用了多步寻优搜索的方法,相比单步搜索生成的航迹更加优化;使用最小转弯半径对生成的折线进行连接,使路径平滑可飞;针对算法局限性,给出一种改进局部最优点的策略。该算法能够较好地满足规划要求。北京航空航天大学曾佳提出了一种满足时序约束的无人机在线协同航迹规划方法。首先采用按时间推进的协同规划机制,解决了在线协同规划中信息交互存在时间间隔的问题;其次通过设计协同函数,采用自主分布计算协同变量的方法解决其时序问题。仿真选取同时到达和按等时间间隔到达两类典型时序问题,结果表明该方法可以快速生成符合协同时序要求的协同航迹。解放军炮兵学院倪敏在对传统算法进行改进的基础上,提出运用支持向量机的思想,建立航迹回归模型。其建模速度快,计算时间少,可扩充性强,能及时为无人机在未知环境中提供实时航线图。西北工业大学田雪涛给出了基于混合整数线性规划技术在模型预测控制框架下进行无人机实时航迹规划的方法。该方法通过将威胁区、速度、加速度以及威胁规避等约束条件转化为能够直接应用在M ILP中的形式,并结合模型预测控制方法来进行规划以满足实时性要求。肖秦琨针对威胁可变及威胁体不尽相同的无人机路径规划问题提出了一种局部路径重规划的算法。算法中,威胁体威胁等级随无人战斗机飞行不断变化,无人战斗机通过多传感器数据融合知识构建动态贝叶斯网络图,获取环境信息,应用V iterbi解码算法获得实时威胁等级,进行局部改进型Voronoi图的重构,以完成局部路径重规划,提高了无人战斗机在实战环境下生存概率。南京航空航天大学安柏义利用Dynapath(动态路径)算法进行参考航线优化,根据局部地形、地貌、障碍、威胁等信息以及飞机机动性能的限制,实时计算出飞行航迹,仿真结果表明该方法可以比较理想地进行航迹点的处理,得到较好的航迹。

国外,K im提出在敌方环境下运用有限的信息进行全自主无人机的实时航迹规划方法,该方法包括两个算法,第一个算法仅考虑非常有限的信息,仅包括无人机当前所处位置的可能存在的威胁;而第二个算法则需利用更多的信息,包括无人机所感知的威胁强度及位置等。两个算法产生一系列安全的路径节点,其风险值低于规定的风险阈值。Kam rani采用序列蒙特卡罗仿真对执行监测任务的无人机进行路径规划。但要求提供足够多的关于目标和环境的先验信息,才可以通过序列蒙特卡罗仿真对目标的未来状态进行评估。Jennings考虑存在随机风场影响下无人机航迹,受风场影响无人机偏离了预规划航迹,通过动态规划法在线插补新的路径节点,由于动态规划算法的内在启发性限制了可选航迹数量,因此,算法在非常快的计算时间内就提供近似最优的航迹。Yang首先使用快速扩展随机树生成防碰路径,该路径由多条直线段连接而成,因此无人机无法按此飞行,然后采用三次Bezier螺旋曲线的G2连续路径算法,将直线用曲线替代,仿真结果表明,该算法较Dubins路径及C1连续三次Bezier螺旋曲线具有更好的效果。Bernhard Weiβ针对未知环境提出一种无人机动态规划算法,无人机飞行航迹由一组可修剪轨迹组成,首先通过当代迭代算法确定了下一代的最佳修剪轨迹,以便降低代价函数值,并通过改变权值,使总的航迹代价最小,最后通过Dijkstra算法获得全局最佳路径。Ducard在未知环境下,降低无人机性能过程中,对无人飞行器航迹实时重规划,从而达到规避障碍等目的。严格地说,该研究提出的是无人飞行器动态导航算法。

综上所述,可用于无人飞行器实时航迹的算法目前主要有:实时A*算法、实时Dynapath算法、连续型粒子群优化、支持向量机(动态路径)、三次Bezier螺旋曲线、Voronoi图等。这些算法除Voronoi图外,其余均基于栅格法,但都存在随着周遭威胁环境复杂度的增加、计算时间也急剧增加的缺点。更重要的是,它们都是以实现代价最小为目标的路径规划,很少考虑到无人飞行器因动力学条件约束生成航迹的不可飞性。以上算法对于这种受无人飞行器自身状态约束的航迹优化问题,处理起来并不容易。通常的解决方法是通过航迹平滑、航迹跟踪技术,对算法生成的航迹进行处理以得到实际可飞航迹,但这却会损失实时性。

5 结束语

无人飞行器在线航迹规划的时效性要求很高,目前还存在以下问题:a)过于简化无人飞行器约束。对无人飞行器动力学约束的考虑过于简单,造成由此规划的航迹往往实际不可飞。b)时效性要求达不到。虽然近年来许多文献提出航迹规划的动态优化方法,但未考虑实战环境下威胁性不断变化的情况。在实时航迹规划中,侦察环境数据常常会实时发生改变,动态规划算法在每次参数发生改变时,必须重新代入模型进行运算,计算时间过长,而达不到及时规避威胁的要求。c)算法模型的失效。无人飞行器航迹规划需要的信息是高维和海量的,而动态规划具有“维数爆炸”特性,这使得在进行算法设计时,简化因素较多、误差较大,建立的模型并不能反映真实的环境,得出的航迹规划不能满足任务要求。

未来在无人飞行器在线航迹规划的发展方向及研究重点主要有:a)开发高效的在线规划算法。要求算法寻优能力强,收敛速度快。需要结合不同算法的优势,提出混合算法,以提高算法的时效性。b)多机在线协同航迹规划。为了提高无人飞行器的作战能力,将具有不同能力的无人飞行器组成网络化无人飞行器群显得非常重要。因此,需要研究无人飞行器群在线协同航迹规划,以实现任务重分配、网络重组、威胁规避及在线自主多机协同作战的功能。■

[1] 高晖,陈欣,夏云程.无人机航路规划研究[J].南京航空航天大学学报,2001,33(2):135-138.

[2] 高晓光,杨有龙.基于不同威胁体的无人作战飞机初始路径规划[J].航空学报,2003,24(5):435-438.

[3] A l-Hasan S,Vachtsevanos G.Intelligent route planning for fast autonomous vehicles operating in a large natural terrain[J].Robotics and Autonomous Systems,2002,40:1-24.

[4] 叶媛媛,闵春平,沈林成,等.基于VORONOI图的无人机空域任务规划方法[J].系统仿真学报,2005,17(6).

[5] 丁晓东,刘毅,李为民.基于动态RCS的无人机航迹实时规划方法研究[J].系统工程与电子技术,2008,30(5):868-871.

[6] 曾佳,申功璋,杨凌宇.无人机在线协同航迹规划时序问题[J].南京航空航天大学学报,2009,41(3):334-338.

[7] 田雪涛,席庆彪.基于混合整数线性规划无人机实时航迹规划[J].计算机仿真,2009,26(5):72-75.