关于Seiffert平均的一个上界估计

佘卫强，何灯



关于Seiffert平均的一个上界估计

佘卫强1，何灯2

（1.漳州职业技术学院，福建 漳州 363000；2.福清市东张中学，福建 福清 350305）

借助于级数理论和多项式的判别系统,给出了Seiffert平均的一个较强上界估计。

Seiffert平均；级数展开；上界估计；不等式

1 引言及主要结果

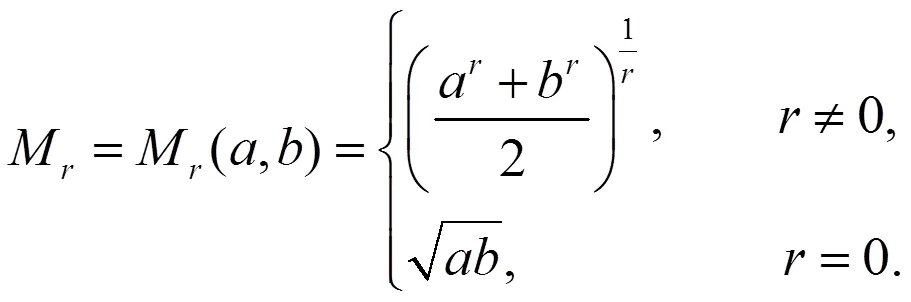
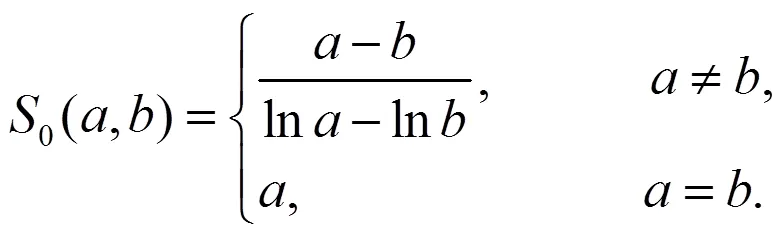
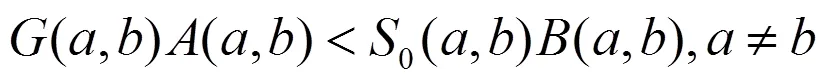
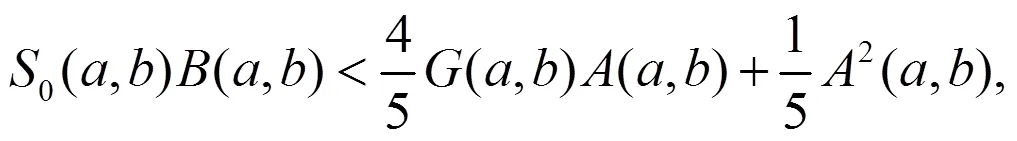
2 引理

定理的证明需要如下引理.

结合引理1和引理2, 上不等式成立, 且易证上不等式的右端小于0.

证明：令

则

综上引理成立.

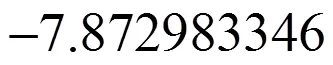
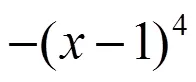
由引理5可得上面不等式成立, 从而定理成立.

[1]Seiffert H J.Ungleicungen fur eunen bestmmten mittelwet[J].Nieuw Archiew vor Wiskunde, 1995,(2)195-198.

[2]匡继昌.常用不等式[M].济南:山东科学技术出版社,2004，第三版：49.

[3]陈传璋，等.数学分析(上)[M].北京:高等教育出版社,1983，第二版:189.

[4]四川矿业学院教学组编.数学手册[M].北京:科学出版社，1978:129.

[5]杨路,张景中,侯晓荣.非线性代数方程组与定理机器证明[M].上海:上海科技教育出版社,1996:137-166.

On Estimations of Upper Bounds of Seiffert’s Mean

SHE Wei-qiang1, HE Deng2

(1.Zhangzhou institute of technology, Zhangzhou, 363000，China;2.Dongzhang Middle School, Fuqing, 350305,China)

In this paper, with the aid of Theory of Series and Polynomial System of criterion,an good estimations of upper bounds of the Seiffert mean are established.

Seiffert’s Mean；Series Expansion；Estimations of Upper Bounds；Inequality

2009－11－16

佘卫强(1981－)，男，福建东山县人，助教，研究生。

O 122.7

A

1673-1417（2010）01-0050-04

（责任编辑：季平）