基于模糊控制的多机系统中励磁与SVC协调控制

赵 虎 杨 伟 赵 猛

（1.南京理工大学动力工程学院，南京 210094；2.江苏省赣榆县供电公司，江苏 连云港 222100）

1 引言

静止无功发生器（Static Var Compensator, SVC）是现代电力系统中一种常用的FACTS设备，它对于维持电压稳定性具有重要的意义。发电机的励磁控制能有效地保证系统的功角稳定，但同时对电压稳定也产生重大影响[1]。通过应用FACTS 设备，可进一步提高系统性能。一般来说，分布于不同地方的发电机励磁控制器与SVC控制器的设计是相互独立的，并未考虑两者之间的相互作用。没有考虑相互协调的控制策略，有可能使它们起相反的作用，甚至引起系统的不稳定。所以要考虑励磁与SVC的协调控制策略[2]。

就励磁与SVC协调控制研究方面而言，文献[3-6]提出了各自的思想和方法。文献[3]提出了一种同步发电机的PSS与SVC协调控制的方法。文献[4]提出了SVC与励磁一种无源性协调控制方法。文献[5]提出了励磁与SVC的鲁棒非线性控制。文献[6]提出了励磁与SVC最优反馈控制方法。这些方法大多针对单机无穷大系统，并未考虑到多台发电机之间的作用。

文中提出了一种基于模糊控制的多机系统励磁与SVC协调控制方法，将发电机励磁与SVC的协调控制策略转化为模糊规则的形式，经过模糊运算，实现了对多机系统的稳定性控制。

2 系统数学模型

2.1 系统接线图

典型的3机9节点系统如图1所示，图中安装了静止无功发生器SVC。

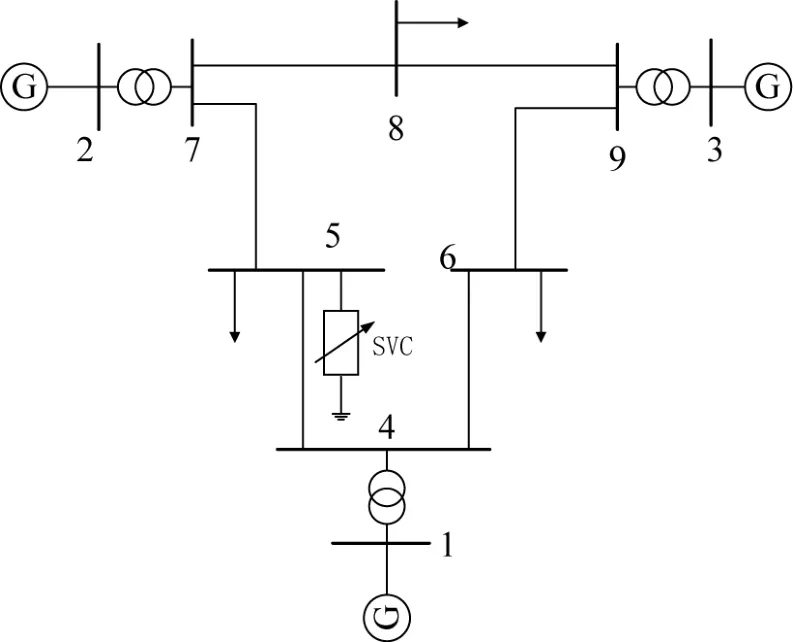
图1 九节点系统

2.2 发电机模型

对于三机系统，发电机模型可描述为

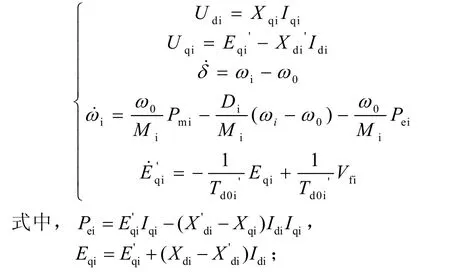
Vfi为励磁系统的输出电压；Pmi为原动机输出机械功率，Pmi＝const.。

2.3 SVC模型

如图2所示，文中采用FC-TCR型SVC，其动态数学模型为

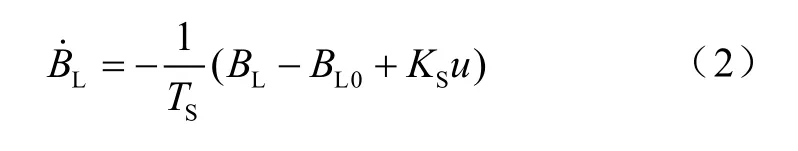
式中，TS为SVC控制器的时间常数；BL为SVC中电感支路电纳；BL0为初始值；u为控制器的增益。

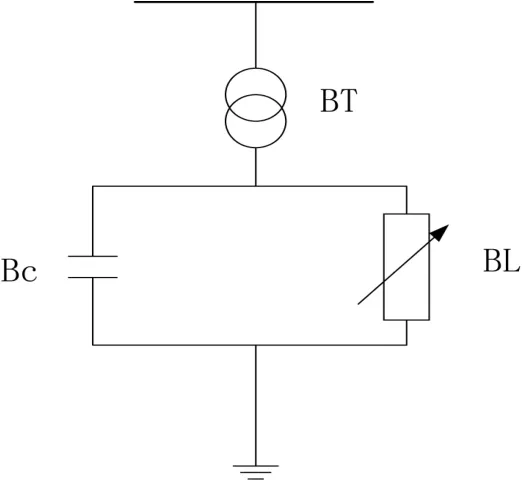
图2 SVC模型

整个SVC的等值导纳为

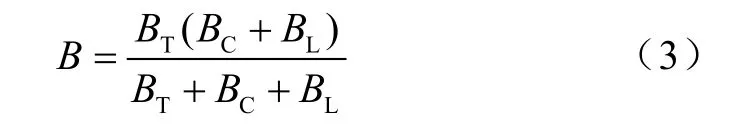
3 模糊协调控制方法

3.1 输入量的模糊化

模糊化就是对论域X上一个确切的输入值x，确定出其相应语言变量在该论域上的语言变量值iA。I的最大数值表示在论域X上语言变量所取语言值iA的个数，或称为模糊化的等级数。取模糊集合A={NB,NM,NS,ZE,PS,PM,PB}。

为了便于工程实现，通常把输入范围人为地定义成离散的若干等级（即离散化），定义级的多少取决于输入量的分辨率。为了标准化设计[7]，M amdani提出将论域范围设定为[-6,6]，将该论域连续变化量离散化，即输入变量Δω、Δω˙的论域取为[-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6]。根据Δω、Δω˙的实际变化范围为[a,b]，将此区间的量转换为[-6,-6]区间变化的量x',采用如下公式[8]：

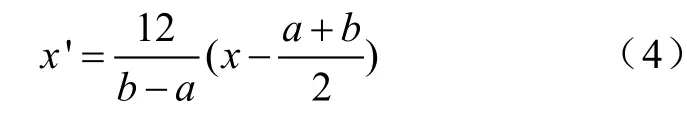
3.2 数据库

数据库存放的是所有输入、输出变量的全部模糊子集隶属度矢量值。输入变量和输出变量分别为Δω、Δ˙和ΔUL、ΔUg，其中ΔUL、ΔUg分别表示发电机的励磁控制量和SVC端口电压控制量。输入函数隶属度函数选为高斯函数，输出函数隶属函数选为三角形函数。表1和表2分别是输入变量和输出变量的模糊量。

3.3 规则库

模糊控制规则表现为一组模糊条件句，它是在总结实际经验的基础上通过统计方法得到的。对于两输入两输出系统采用If A And B Then C And D类型的模糊语言实施控制策略，如If Δω=NB And Δ˙=NB Then ΔUg=PB And ΔUL=NB。根据专家知识、实践经验以及相关参考文献[9-14]，总结出的模糊控制规则如表3和表4所示。

3.4 反模糊化

模糊推理的结果一般都是模糊值，不能直接用来作为被控对象的控制量，需要将其转换成一个精确量，这个过程称为反模糊化。采用所有解模糊化方法中最为合理的方法——重心法。该方法的数学表达式为

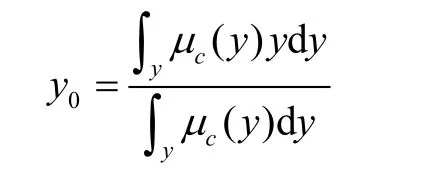
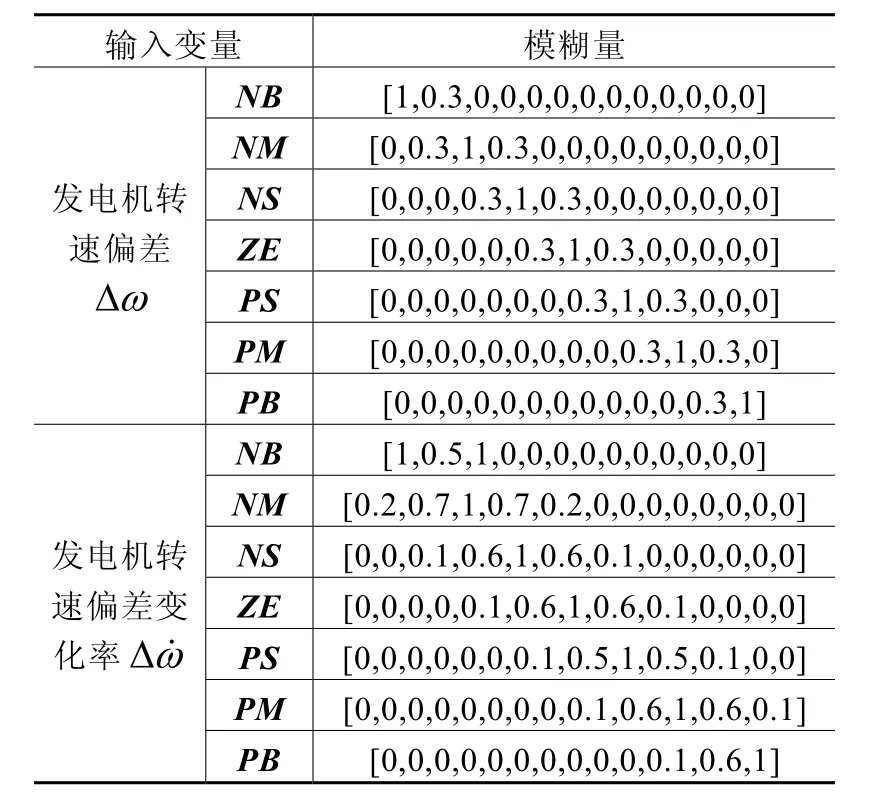
表1 输入变量的模糊量

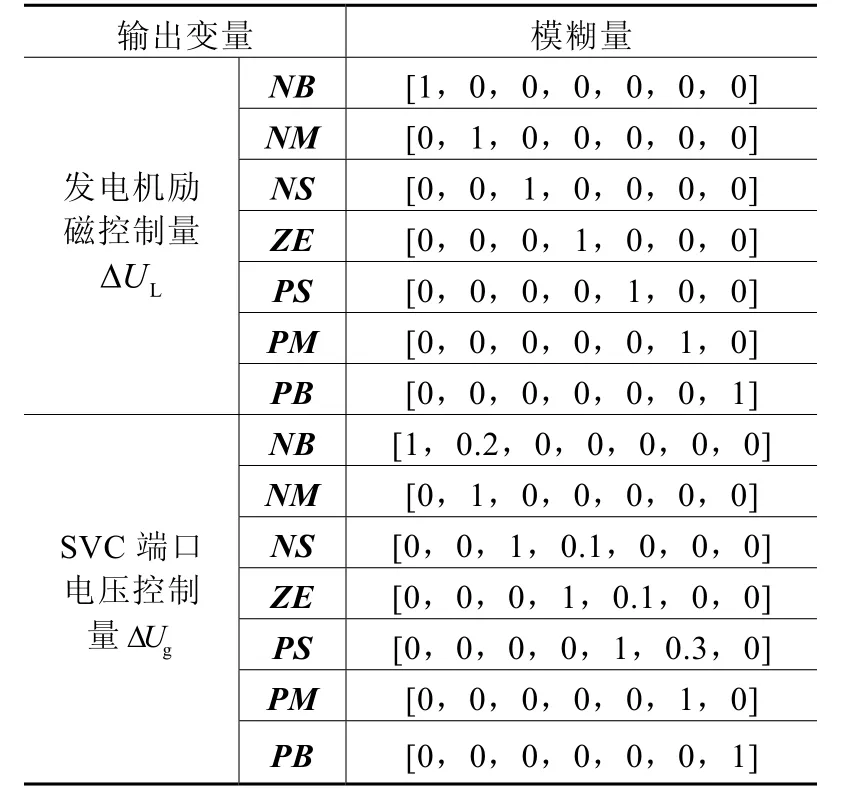
表2 输出变量的模糊量

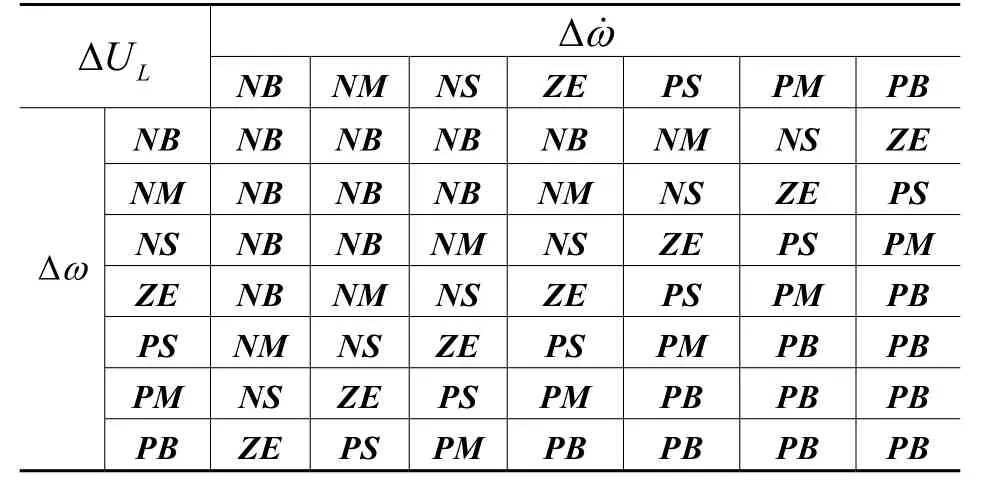
表3 励磁控制量的模糊控制规则表

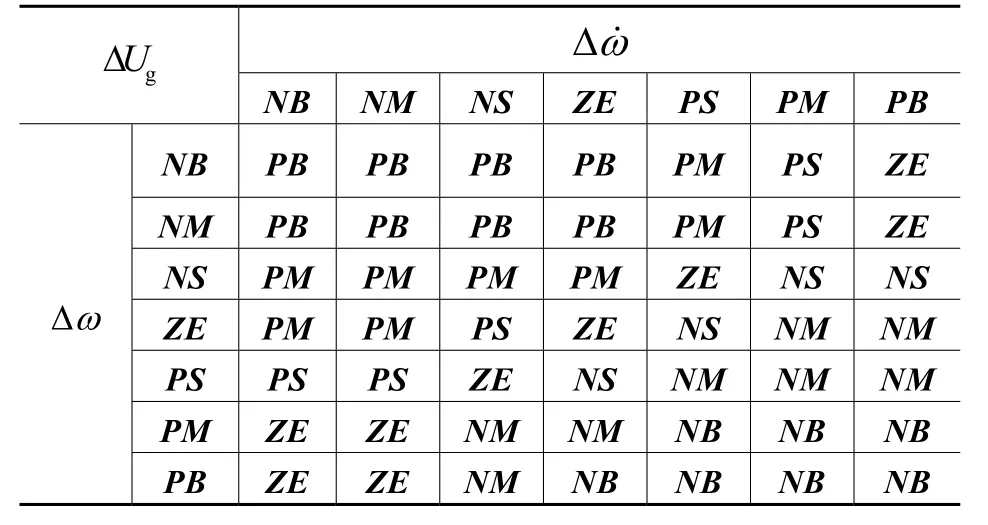
表4 SVC端口电压控制量的模糊控制规则表

3.5 模糊控制子程序的设计

模糊控制子程序如图3所示。

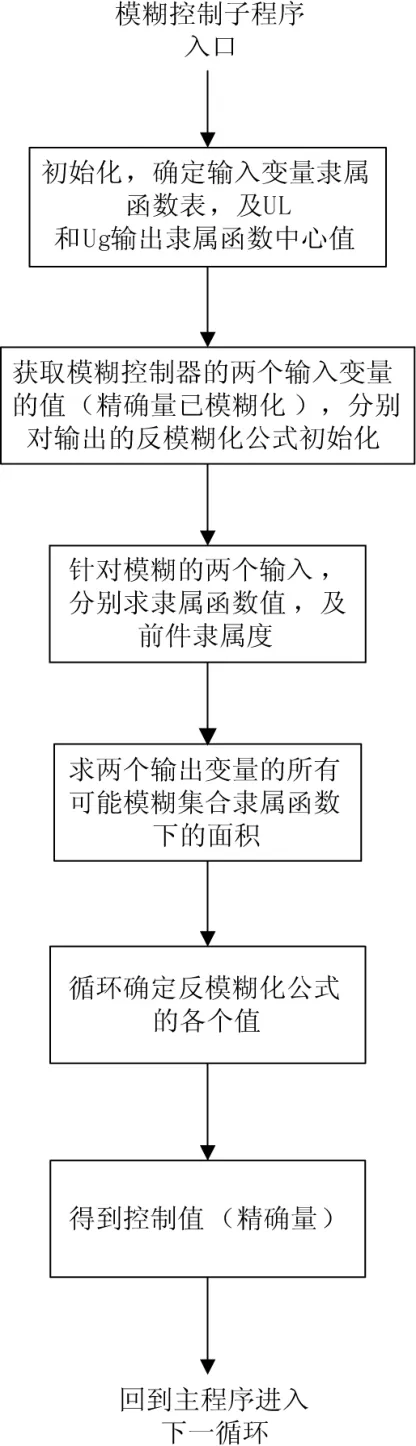
图3 模糊控制子程序

4 仿真分析

以上述3机9节点系统作为研究对象，研究模糊控制对励磁与SVC的协调作用。系统如图1所示，具体数据详见文献[15]。

为了体现控制效果，这里采用常规的AVR/PSS励磁控制器和PID SVC控制器[16]作为比较对象。各台发电机采用的PSS参数如下表所示。SVC 的容量设成50M var。节点5的稳态电压为0.9956（pu）。

表5 PSS参数

（1）假设在0s时，节点7发生三相短路，0.08s时通过切除节点5-7之间的一条线路使故障消失。图4、图5为发电机2、3相对于发电机1的功角变化曲线。图6为节点5的电压变化曲线。

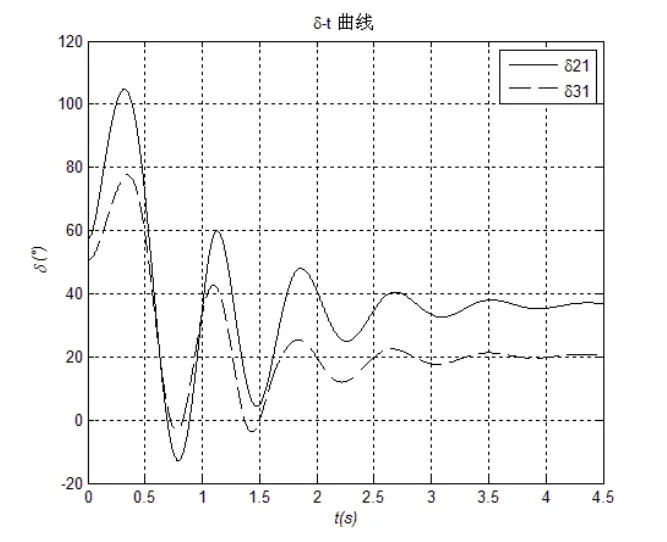
图4 常规控制下发电机功角响应曲线（故障1）

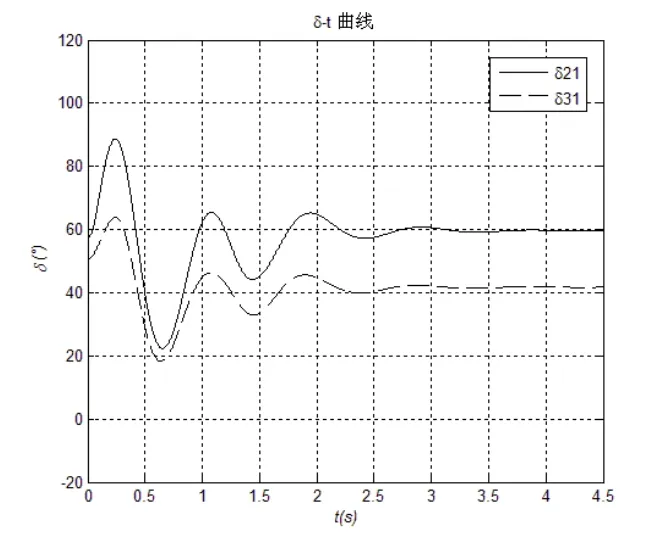
图5 模糊控制下发电机功角响应曲线（故障1）

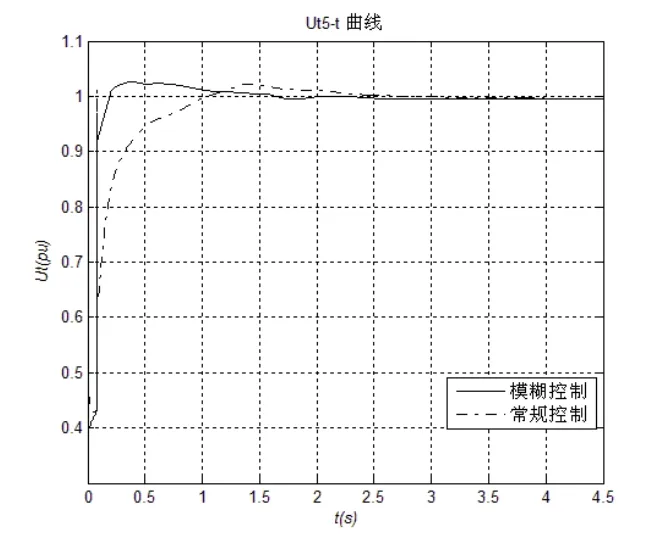
图6 节点5的电压曲线（故障1）

可以看出，在变压器低压侧端发生三相短路的故障情况下，从图5可知基于模糊控制的协调控制，发电机功角振荡幅度较小，第一摆转子相对角δ21小于70°，δ31不到50°，3s后就能维持在一定值，保持稳定；而常规控制方式下，第一摆转子相对角δ21将近120°，δ31将近80°，需要4s才能基本保持稳定。图6，节点5的电压对于模糊控制而言，一方面短路后电压峰值很小，系统的超调量也不大，另一方面系统能快速恢复稳定的运行状态，协调控制只需1.5s的时间，恢复到稳态电压，而常规控制需要2.5s才能恢复。因此，基于模糊控制的励磁与SVC协调控制可以大大提高系统的暂态稳定水平。

（2）假设在0s时，节点3处发生三相短路，0.10s时故障消失。图7～9展示了相应的变化曲线。

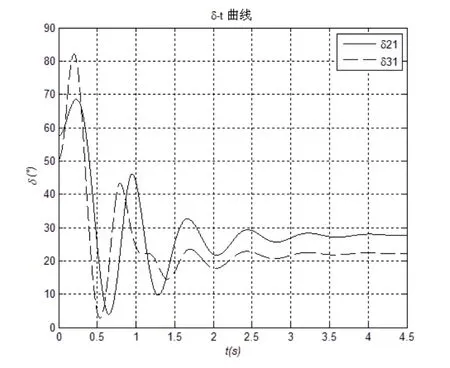
图7 常规控制下发电机功角响应曲线（故障2）

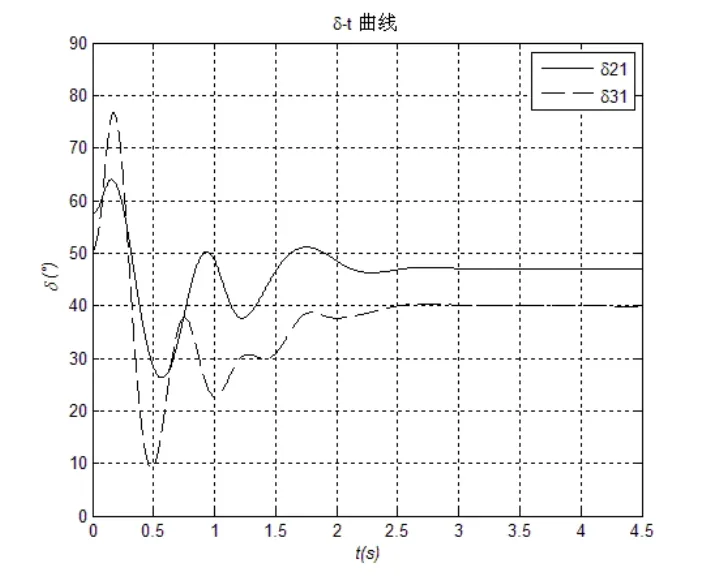
图8 模糊控制下发电机功角响应曲线（故障2）

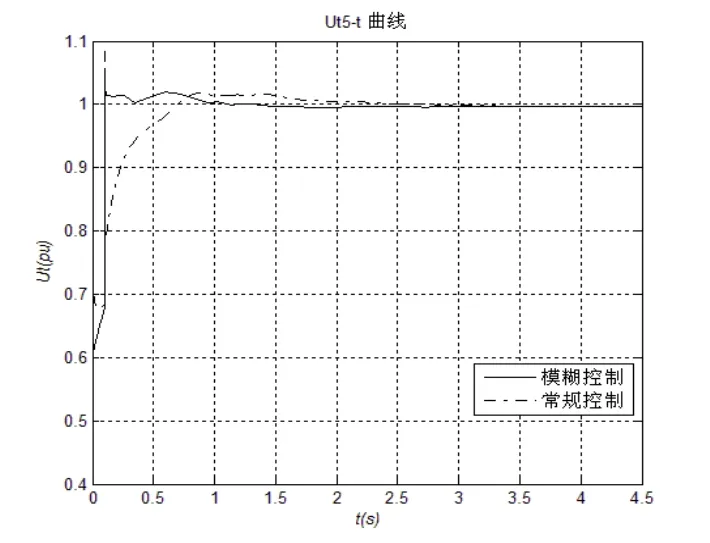
图9 节点5的电压曲线（故障2）

可以看出，在3号发电机机端发生三相短路的严重故障情况下，从图8可知基于模糊控制的协调控制，发电机功角振荡幅度较小，抑制第一摆的能力依旧较强；而常规控制方式下，第一摆转子相对角δ21接近70°，δ31将近80°。图9，相对于常规控制而言，基于模糊控制的励磁与SVC协调控制仍然显示了短路后电压峰值很小和快速恢复到稳态的特点。

5 结论

通过以上讨论可以得出以下结论：

（1）所提出的基于模糊控制的多机系统励磁与SVC协调控制方法，在系统受到大干扰的情况下，可以有效地提高电力系统的暂态稳定性。

（2）在三机系统数学模型的基础上用模糊控制的方法，对发电机励磁和静止无功发生器SVC的协调控制进行了研究。将协调控制策略转化为模糊规则的形式，分别得出了发电机励磁与SVC的协调控制规则。最后通过与常规控制模式下的仿真结果对比，证明了文中提出的基于模糊控制的协调控制方法的正确性和有效性。

[1] 刘辉,李啸骢,韦化,等.基于目标状态方程的非线性预测励磁控制器的设计[J].中国电机工程学报,2005,25(17): 27-31.

[2] L.Cong, Y.Wang, D.J.Hill. Coordinated Control Design of Generator Excitation and SVC for Transient Stability and Voltage Regulation Enhancement of Multi-machine Power Systems. International Journal of Robust and Nonlinear Control 2004,14:789-805.

[3] Mahran AR, Hogg BW, El-Sayed ML. Coordinated control ofsynchronous generator excitation and static VAR compensator. IEEETrans Energy Conv 1992,7:615–22.

[4] 阮映琴,王杰.SVC与发电机励磁无源协调Backstepping控制[J].电工技术学报,2007,6(22): 135-140.

[5] Wang Y, Tan YL, Guo G. Robust nonlinear coordinated generator excitation and SVC control for power systems.International Journal of Electrical Power and Energy Systems, 2000, 22(6):187-195.

[6] Rahim A, Nassim i S. Synchronous generator damping enhancement through coordinated control of exciter and SVC. IEE Proc Gener Transm Distrib 1996,143(2):211-8.

[7] 姜惠兰,魏强,唐晓骏.基于模糊神经网络的发电机励磁控制器的研究[J]. 电网技术,2005,29(1):50-55.

[8] 席爱民.模糊控制技术[M].西安:西安电子科技大学出版社,2008.

[9] 金广厚,宋建永,程晓荣.基于模糊神经网络的电能质量指标的经济性评估[J]. 电力系统及其自动化学报,2004,16(6):18-23.

[10] Linkens D A, Nyongesa H O. Learning Systems in Intelligent Control: an Appraisal of Fuzzy, Neural and Genetic A lgorithm Control. IEE Proc. of Control Theory Appl, 1996, 143(4):367-386.

[11] 伍世虔,徐军.动态模糊神经网络—设计与应用[M].北京: 清华大学出版社,2008.

[12] 高俊莹, 徐建军, 许爱华,等. 风能利用系数模糊控制策略的研究[J].电气技术, 2009 (8):36-42.

[13] D.Z.Fang, Yang Xiaodong, T.S.Chung. Adaptive Fuzzy-Logic SVC Damping Controller Using Strategy of Oscillation Energy Descent.IEEE Transactions on Power System, 2004,8(19):1414-1421.

[14] 贾媛, 佟威, 李红莲,等. 基于模糊自适应控制的电动机软起动仿真[J].电气技术, 2009 (9):63-65.

[15] 王锡凡,方万良,杜正春.现代电力系统分析[M].北京:科学出版社,2003.

[16] 彭志炜,胡国根,韩祯祥.基于分叉理论的电力系统电压稳定性分析[M]. 北京:中国电力出版社,2005.