基于T-S模糊策略永磁直线同步电动机直接推力控制
杨俊友 赵 菲 刘启宇
(沈阳工业大学电气工程学院,沈阳 110870)
1 引言
在许多工业领域中,被控对象的运动路径通常是直线的形式,然而长期以来人们一直借助旋转电动机来实现直线运动。直线电动机是一种利用电能产生直线运动的电机,可以直接驱动机械负载作直线运动。永磁直线同步电动机(PMLSM)具有推力高、损耗低、电气时间常数小、响应速度快等特点,在很多场合日益受到重视,并具有广阔的应用前景。
直接推力控制最广泛应用于PMLSM中,是一种具有高动态性能的新型交流伺服驱动方式[1-3],其实质是通过选择合适的电压矢量来迫使磁链逼近圆形。传统直接推力控制无法使磁链形成正圆,只能使磁链控制在滞环中,因此直接推力控制存在着推力、磁链脉动大的缺点。
模糊控制技术具有语词计算和处理不精确性、不确定性和模糊信息的能力,近年来已被证明是解决许多复杂建模和控制问题的一种有效方法[4]。T-S型模糊系统可以方便的进行非线性系统建模和非线性控制系统设计,克服了M amdani型模糊系统输出必须解模糊的缺点。T-S模糊模型的后件输出为线性关系,其推理方法表达记忆能力好,所得出的推理结果为清晰量,可以直接作为控制量,无须专门解模糊处理,简化了其他模糊控制方法解模糊的过程。目前,对于T-S模糊控制的研究尚处在理论中,主要应用在转台控制中。
本文将T-S模糊控制策略首次应用到PMLSM直接推力控制系统,在所设计的Mamdani控制器基础上采用辨识的方法将离散的输出转换为线性输出的T-S模糊控制策略。简化解模糊过程,改善系统的控制效果。
2 永磁直线同步电动机数学模型
不考虑端部效应的情况,根据功率不变原理可得d-q坐标系下的电压磁链方程分别为[5]

其中,p=d/d t
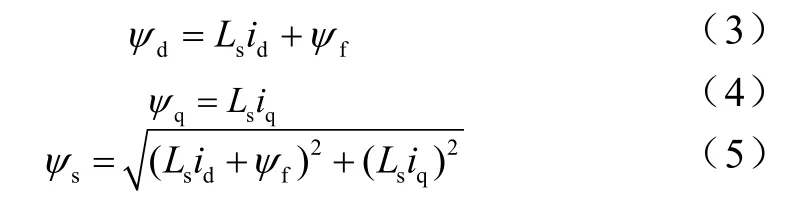
其中,ωr=πv/τ,v 为直线电机的线速度。

电磁功率表达式为

推力Fx表示为

其中,ψPM为总磁势
空间向量方程如下
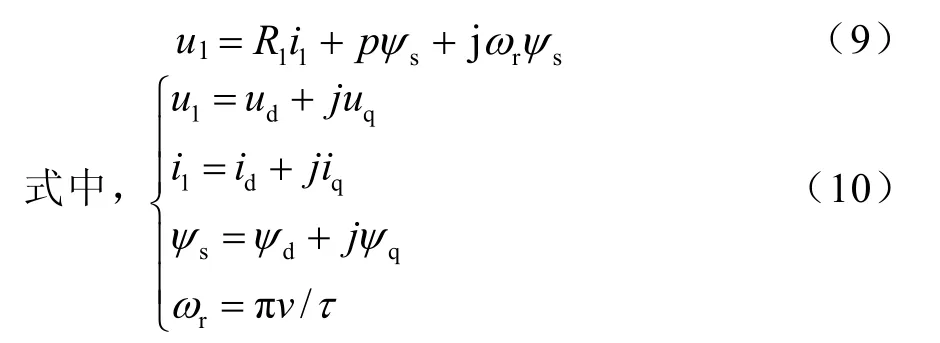
机械运动方程
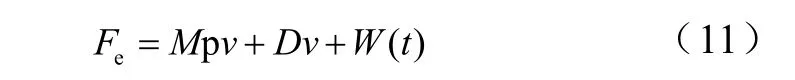
其中D为粘滞摩擦系数,W(t)为外部扰动,M为动子质量。
3 M am dani模糊控制器
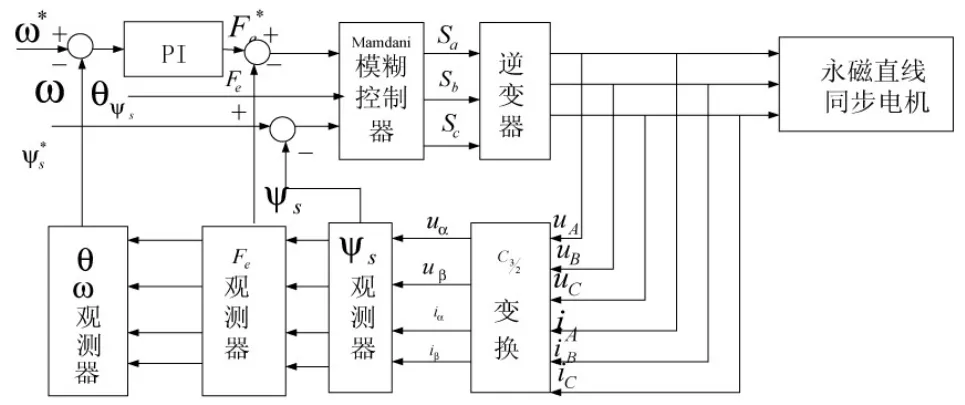
图1 基于T-S模糊控制的直接推力控制系统
3.1 磁链、推力的模糊化及其隶属度函数
取推力误差eFe与磁链误差为eΨs控制器输入

Mamdani模糊控制器采用二维输入,一维输出。输入量为推力误差eFe,磁链误差eΨs,输出量为电压矢量对应的逆变器开关状态[6]。将eΨs、eFe大小进行区分,根据不同等级作不同决策来优化空间电压矢量的输出选择,两个模糊变量都划分为四个模糊子集,语言值均取为{NB,NS,PS,PB},隶属函数选用三角形。两个输入量推力误差eFe,磁链误差eΨs的隶属函数如图2~4所示。

图2 推力误差隶属函数

图3 磁链误差隶属函数

图4 输出隶属度函数
3.2 模糊控制规则及模糊决策
模糊控制器根据当前推力误差及磁链误差的模糊分级来决定是应该增大推力还是减小推力,以及是增大磁链还是减小磁链[7]。根据各个扇区所应施加的电压矢量,可以把电压矢量的作用分为四种:
当电压矢量为Ⅰ时增大转矩、增大磁链;为Ⅱ时减小转矩、增大磁链;为Ⅲ时增大转矩、减小磁链;为Ⅳ时减小转矩、减小磁链。
建立16条模糊控制规则,如表1所示。

表1 控制规则表
根据这16个模糊规则构成系统总的模糊蕴涵关系R为
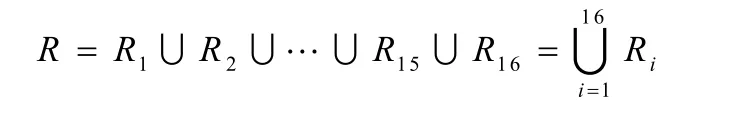
采用的模糊推理规则如下:
IF eΨs=EKi,and eFe=EFjTHEN U=Vn, i=1~4,j=1~4,n=1~6式中EKi,EFj分别为磁链差值、推力差值和次级磁链位置,Vn为单值模糊电压矢量。
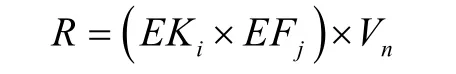
然后由测得的磁链差值EKi、推力差值EFj、通过模糊矩阵R可以得到电压矢量由模糊输出表达式
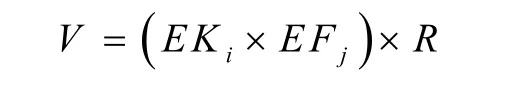
将模糊控制器的输出与矢量表相结合,采用单点化输出简化解模糊过程来确定在不同的扇区应对推力转矩及磁链控制作用的电压矢量。表2为电压矢量选择表。

表2 电压矢量选择表
4 T-S模糊控制器
4.1 T-S模糊模型
T-S型模糊系统数学描述为[8]
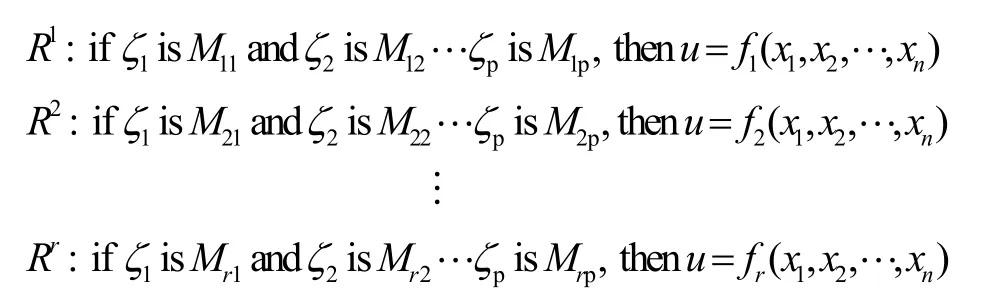
其中,Mik,i=1,2,··,p,为模糊集,r为系统的模糊规则数目;x(t)=(x1,x2,··,xn)T∈Rn,ζ(t)=(ζ1,ζ2,··ζp)T∈Rp为模糊系统的状态变量和前提变量;u(t)∈Rm为输出变量。在实际的系统中,fi(x1,x2, ··xn),i=1,2, ··,r可采用多项式或状态方程。
对于T-S类型的模糊系统,如果选择不同的模糊推理方法以及模糊化和去模糊方法,则控制器的算法和控制效果也不相同[9]。
4.2 磁链、推力的模糊化及其隶属度函数
本文中设计的T-S模糊控制器采用二维输入,一维输出。输入量为推力误差eFe,磁链误差eΨs,输出量为电压矢量对应的逆变器开关状态[10]。输出表达式为u=peFe+qeΨs+k。在考虑到运算方便、性能熟悉等因素并参考专家经验,两个输入量推力误差eFe,磁链误差eΨs的隶属函数同Mamdani控制器相同。
4.3 模糊控制规则及模糊决策
为简化解模糊过程T-S模糊控制器输出采用系统辨识的方法来实现模糊控制器清晰化过程。二维T-S模糊控制器主要完成参数辨识。根据系统的大量输入、输出数据采用“最小二乘”等方法确定满足T-S关系式的常数p、q和k的取值。采用最小二乘法所取的模糊控制器的输入输出进行辨识,确定出满足T-S关系式的常数p、q和k[11]。最小二乘法是系统参数辨识中最基本最成熟的方法由数学家高斯于1795年首先提出。假定被控系统的结构如图5所示。

图5 一般被控系统
其数学模型可用线性方程(14)描述
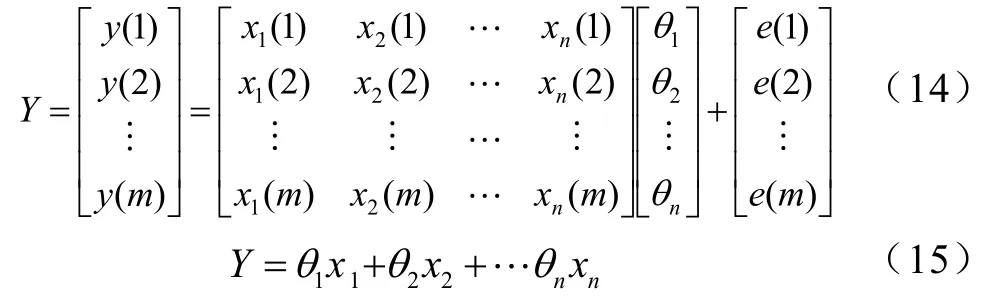
其中,Y为输出量;x1、x2、··、xn为输入量;θ1、θ2、··θn便是待辨识的参数。
由于实际系统存在误差,更精确的系统模型可以表示为

若分别在t1、t2、··tm对输入量x,输出量y进行m次观测,并且将系统数学模型写成矩阵向量的形式,即

求参数θ的估计值θ∧,使性能指标J为最小,当XTX为非奇异矩阵时,可推导得被称为参数θ的最小二乘法估计[12]。

测得一组系统参数见表1。最小二乘法参数辨识后得出p=-0.0002,q=0.0041,k=0.0000073。根据最小二乘法通过相同的辨识方法最后产生16条模糊控制规则,模糊规则见表2。

表3 所测一组系统输入输出参数
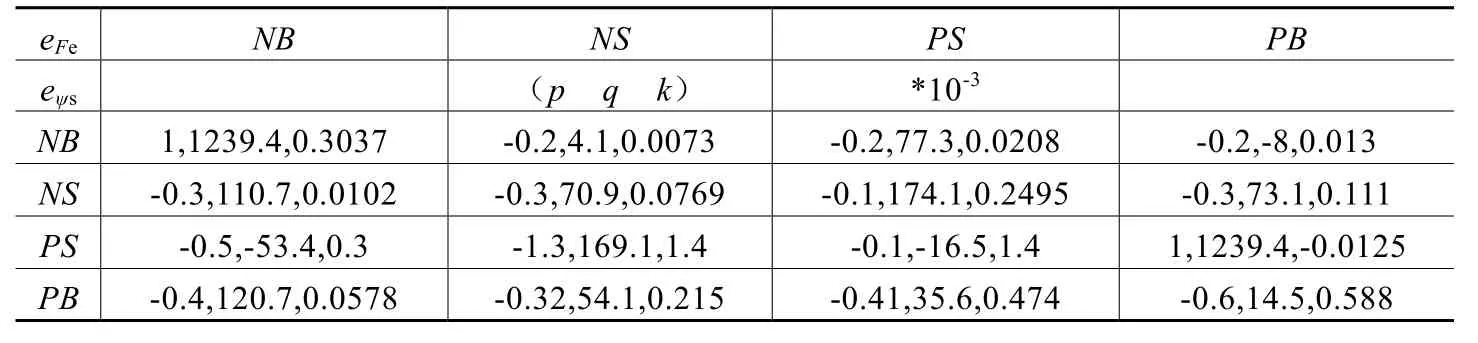
表4 模糊规则表
采用加权求和法求出模糊控制器的总输出U。设第i条规则输出的结果为ui,它的权重为ωi,则总输出为[11]
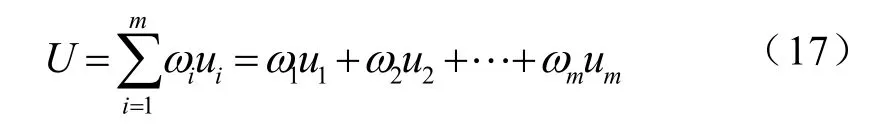
5 仿真分析
将所设计的T-S模糊控制器加入直接推力系统中,并在M atlab环境下仿真。永磁同步直线电动机参数如下:Rs=2.1Ω,Ld=Lq=L=16.3mH,ψs=0.211Wb,M=25kg,Ts=1μs。在该电机参数下进行带负载仿真,负载为200N,电动机在0时刻带负载起动,阶跃输入为0.1m/s,定子磁链给定为0.175Wb。仿真结果如图5~ 9所示。

图6 基于M am dani控制的次级磁链轨迹
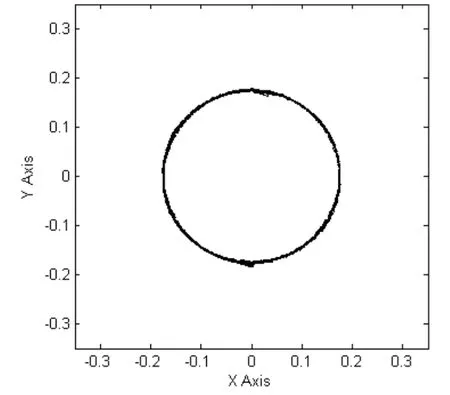
图7 基于T-S控制次级磁链轨迹

图8 Mam dani控制策略下的速度响应
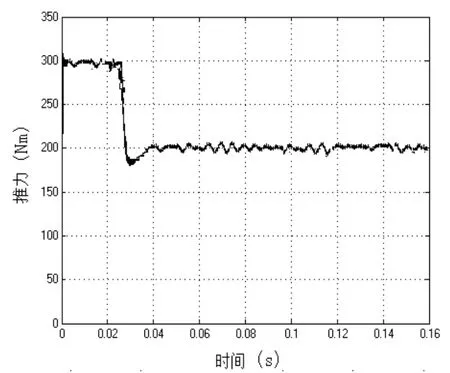
图10 M am dani控制策略下的推力响应
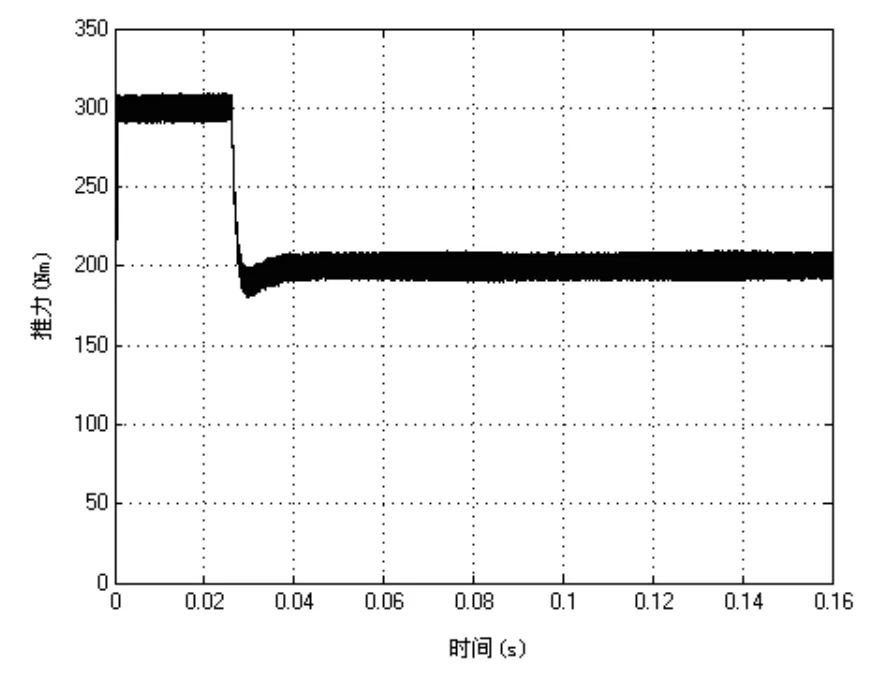
图11 基于T-S模糊策略下的推力曲线

图12 基于M am dani模糊策略下推力曲线局部放大
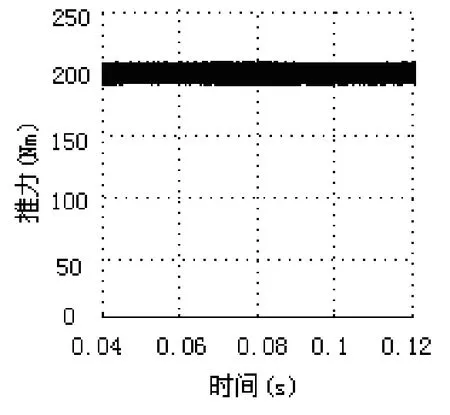
图13 基于T-S模糊策略下推力曲线局部放大
Mamdani模糊控制策略可以实现推力脉动的改良,解模糊过程随机性大,易使系统响应发散。但是采用辨识之后的T-S模糊控制策略,将输出又重新合理化分级细化空间电压矢量的选择,很好地减小推力有利的改良速度响应。系统的稳定性,鲁棒性得以保证。
采取T-S模糊策略的系统次级磁链为圆形,在电动机空间形成了圆形旋转磁场。其推力脉动获得明显改善,从而改善了其最终的输出特性。
从仿真结果计算出速度响应的超调量为2.6%,阶跃时间为0.028s,调节时间为0.044s,可以看出添加了T-S模糊控制器的永磁同步直线电机直接推力系统能够达到输出跟随输入,速度响应快。
6 结论
从仿真结果可以看出,采取T-S模糊控制策略后的直接推力控制系统的次级磁力轨迹基本为正圆形,达到直接推力控制所要求的磁链轨迹效果。速度响应迅速并且超调量小于5%,达到速度响应的要求。与Mamdani模糊策略相比推力响应迅速稳定,脉动得到了很好的改善,脉动明显减小。因此加入T-S模糊策略可以改善原系统的控制效果。
[1] 邹积浩.永磁直线同步电机控制策略的研究[D].杭州:浙江大学,2005.
[2] 叶云岳.直线电机原理与应用[M].北京:机械工业出版社,2000.
[3] 叶云岳.直线电动机技术[J].电气时代,2002,(9): 12-13.
[4] 崔涛,赵莉.模糊控制理论和应用的发展概况[J].自动化仪表,2002,23(7):1-3.
[5] 郭庆鼎,王成元,周美文,等.直线交流伺服系统的精密控制技术[M]. 北京:机械工业出版社, 2000:44-46.
[6] 尹建寨. 直线同步电机直接推力控制方法的研究与实现 [D].四川:西南交通大学,2006.
[7] 王成.模糊系统的稳定性研究[D].武汉:武汉理工大学,2006.
[8] Tanaka K, Sugeno M. Stability analysis and design of fuzzy control systems[J]. Fuzzy Sets and Systems,1992, 45: 135-156.
[9] 修智宏,任光.T-S模糊控制系统的稳定性分析及系统设计[J].自动化学报,2004,20(2):731-741
[10] 王华, 邹积浩, 基于模糊逻辑的直线永磁同步电机直接推力控制[J]. 电子器件, 2007, 30(6):2280-2283.
[11] 石辛民,郝整清.模糊控制及其仿真[M].北京:清华大学出版社;北京交通大学出版社,2002:118.
[12] 严运国,杨辉.最小二乘法参数辨识及其微机实现[J].福建电脑,20056,(6):90-92.

