加权Voronoi图重心在公共设施选址中应用的研究

庞 慧 郑 铮 赵 巍

1.河北建筑工程学院计算机系;2.唐山师范学院计算机系

0 引 言

在计算几何中,Voronoi图是对平面n个离散点而言的.它把平面分为几个区,每一个区包括一个点.该点所在的区是到该点距离最近点的集合.Voronoi图是一种平面分割图,它的剖分结果能够很好地表达点与点之间的邻近关系以及点的影响范围等重要的空间信息.在计算几何中,Voronoi图理论上成功地解决了找最近点、求最大空圆、求最小树等问题.另外Voronoi图还被广泛地应用于计算机辅助设计、地理信息处理、计算机图形学、模式识别、机器人、生态研究、城市规划、最优配置、物理、化学等方面.

普通Voronoi图是将含有n个离散点的平面分割为n个区,每个区含有一个点,该点所在区中的所有点到该点的距离小于到其他任何一点的距离.每个离散点被称作一个生成元,每个区被称作这个生成元的Voronoi区.两个相邻生成元具有公共的Voronoi边.

在实际应用中,普通Voronoi图所表现出来的Voronoi图的区域划分有时是不准确的.因为在实际生活中,普通Voronoi图区域划分的时候并未考虑生成元的一些影响因素,它所表现的是一种同等对待所有生成元的一种理想状态,所以为了能够使Voronoi图更好地应用于实际中需要引入加权Voronoi图.加权Voronoi图是为每个生成元加上一个权重,距离的测算是用点到点的距离除以这个权重,这样得出加权Voronoi区域.

随着社会的进步,城市必定会进一步建设与规划.对于公共设施的选址更是城市规划中经常遇到的问题.对于公共设施的选址必须既方便居民使用又要考虑避免出现设施位置选择不当而导致的资源浪费.而Voronoi图的每个Voronoi区域都是该区生成元的影响范围.这样就可以利用Voronoi图来解决公共设施的选址问题是非常合适的.通常认为公共设施的选址越接近平面图形的重心则它的选址越趋近合理.这样必须要找出确定Voronoi区域重心的方法以更准确地找到选址的位置.普通Voronoi图区域的重心体现了几何平面的重心位置.而实际应用中由于某个区域的影响范围受到各种因素的影响,例如人口密度、地形地况、设施自身条件等因素.所以某些时候要综合考虑这些影响因素来确定一个权重,从而根据权重得到加权Voronoi区域.加权Voronoi区域的重心是一个综合影响因素得到的重心,在某些时候这个重心位置是更符合实际生活的的最佳选址位置.

1 普通voronoi图和加权voronoi图

1.1 普通voronoi图的定义

普通Voronoi图由给定的一个有限点集,根据最近成员的位置关系将空间分成一些小区域,平面上一个点集的Voronoi图是对平面的一个划分.其中每个分区表示一些点的集合,这些点到的一个元素比到其它元素距离更近.其数学定义如下:

1定义1 设为平面上的点集,将由)所给出的对平面的分割,称为以为生成元(或母点)的Voronoi图,简称为Voronoi图(图1),其中d(p,pi)为p和pi间的欧式距离,图中的边界称为生成元pi和pj之间的Voronoi边,不同Voronoi边的交点称为Voronoi顶点.如图1所示,其中图中黑点为生成元,细线为Voronoi边.

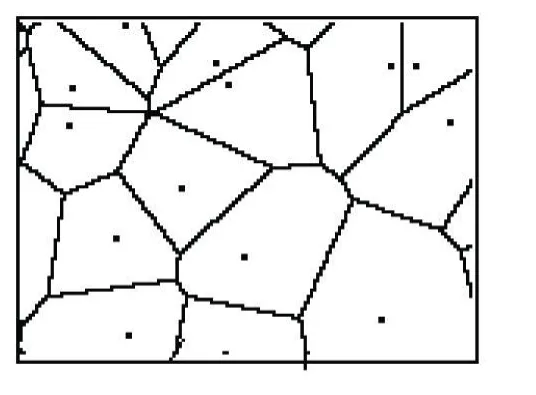
图1 欧氏距离下的Voronoi图

该定义中p和q之间的距离d(p,q)可以是欧氏距离,也可以是其它距离(如L1距离等).

1.2 加权Voronoi图

加权Voronoi图是点生成元加权Voronoi图的简称.

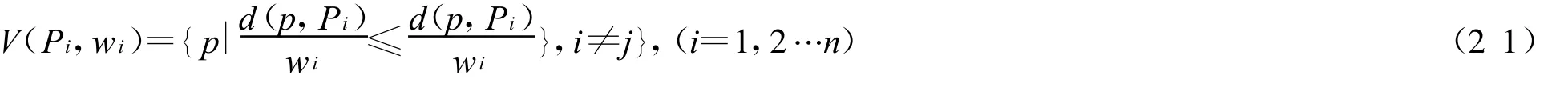
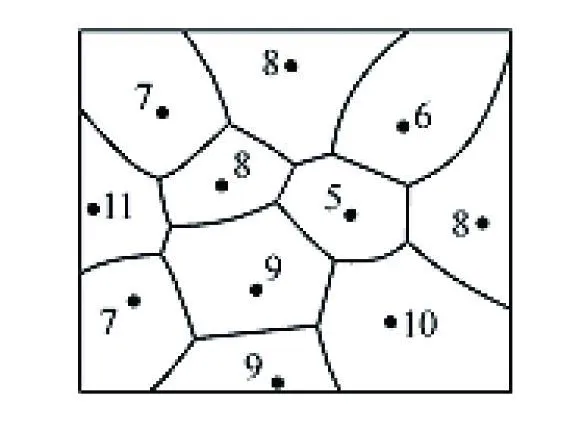
图2 加权Voronoi图

2 权重的确定及普通voronoi区域和加权voronoi区域的区别

当有多个因素来确定权值时需要用层次分析法来进行计算.我们以联通营业厅的选址为例.每个营业厅的覆盖区域受交通便利情况、营业厅面积、基础硬件条件、服务水平、人口数量五个因素影响.层次模型如图3所示.

图3 层次结构模型

专家分别对五个营业厅的五个因素进行评分后,填写比较表构成判断矩阵.经过计算后五个影响因素的权重比例如表1所示.

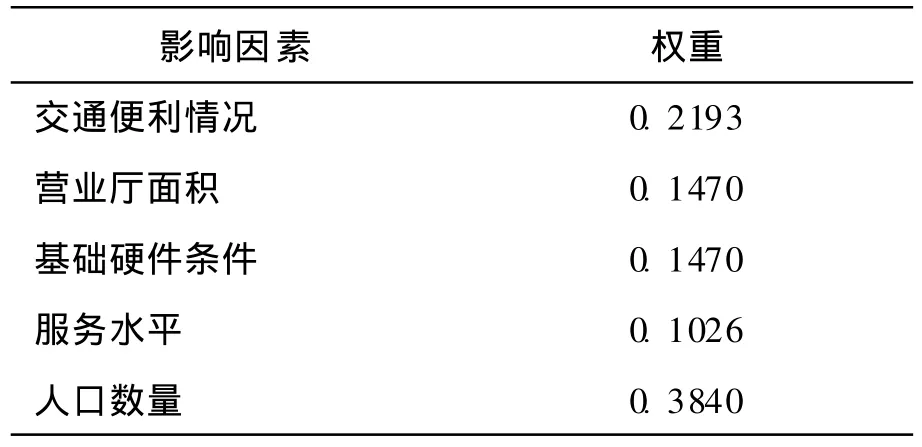
表1 各影响因素权重表

五个营业厅的权重如表2所示

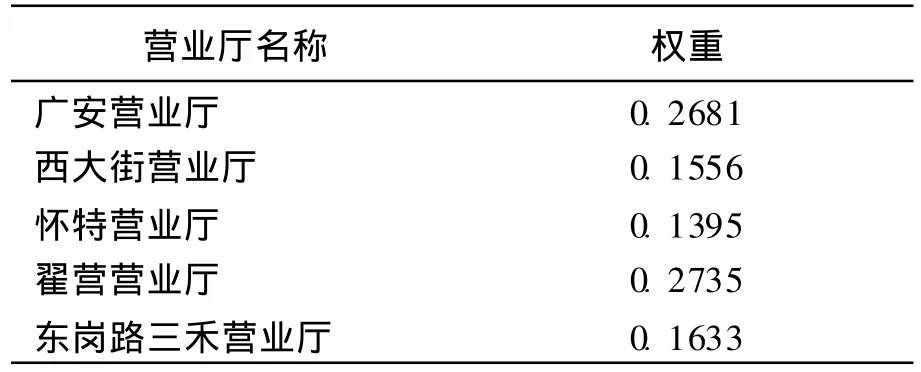
表2 五个营业厅的权重表

这样根据表2所示确定了五个营业厅的权值.将利用层次分析法得到的权值乘以100倍作为每个营业厅的权值.图4中●是营业厅的假设选址位置,以这个位置为生成元,以表2权值的100倍为权值,利用离散的方法生成加权Voronoi图的区域划分结果如图4所示,而图5是不考虑权值的普通voronoi图的区域划分结果.

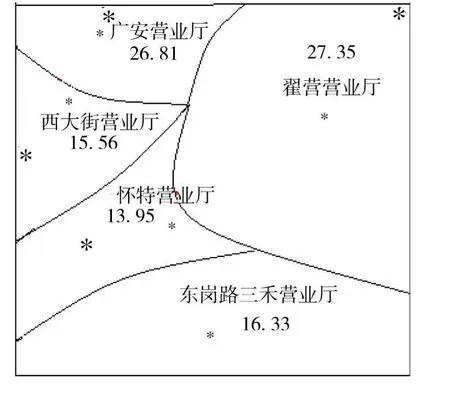
图4 加权Voronoi区域及重心示意图

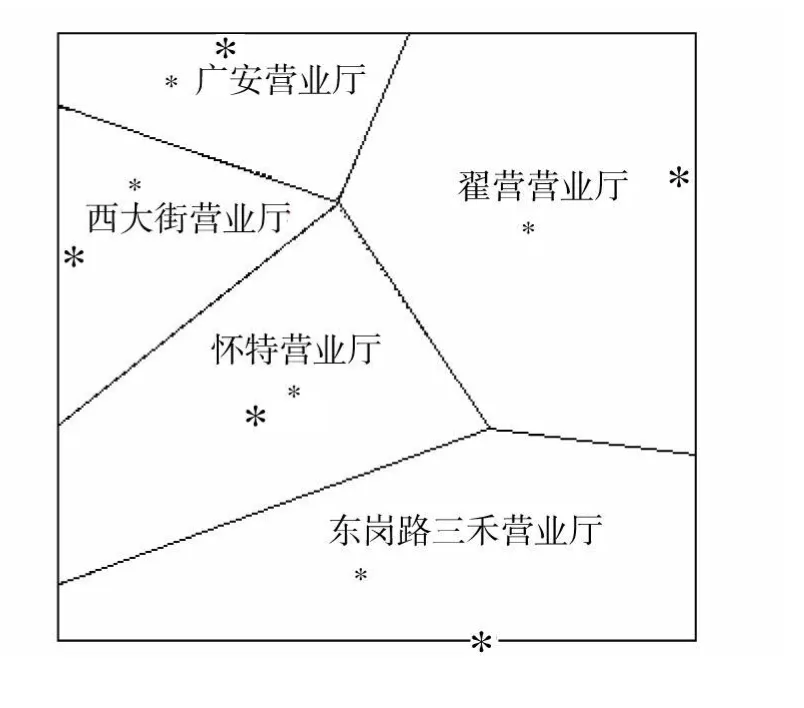
图5 普通voronoi区域示意图

区域内的居民到各自加权Voronoi区域的生成元营业厅缴费为最佳.在图5的普通Voronoi区域划分图中,怀特营业厅区域上部靠近voronoi边的居民原处于怀特营业厅的影响区域.如单纯考虑地理位置而不考虑其他因素的话则上述居民到怀特营业厅缴费是最佳选择.但实际生活中由于要考虑例如人口数量等众多影响因素所以加权Voronoi区域与普通Voronoi区域有所区别.例如实际生活中怀特营业厅所覆盖的区域由于居民区较多、道路不是很畅通等因素影响所以该营业厅的权值较小,故怀特营业厅的加权Voronoi区域比普通Voronoi区域面积有所减少.这样在实际生活中普通voronoi图中怀特营业厅区域上部靠近voronoi边附近的居民到西大街营业厅缴费比到怀特营业厅缴费更合理,如图4所示这些居民已经划归西大街营业厅的范围了.

3 重心的确定及作用

3.1 Voronoi图重心的公式

以图4为例,我们要设法求出每个区域的重心.因为重心位置是这个区域的最佳选址位置.我们知道平面上的n个质点P1、P2、…PN,它们的坐标分别(X1,Y1),(X2,Y2),…(XN,YN),质量分别为M1、M2、…MN,G(X,Y)为重心,则有

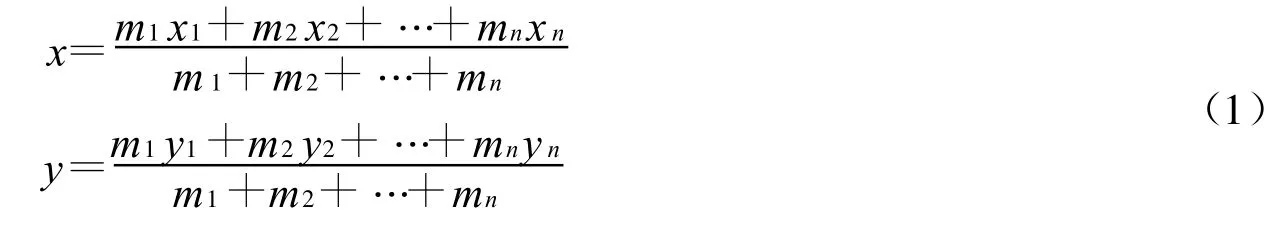
当这n个质点的质量相等时,则可得到平面上n个几何点的重心坐标:

公式(2)同样适用于凸多边形.Voronoi区域是一个凸多边形,在用程序实现的时候这些区域都是由像素点构成的.如果将整个屏幕看做一个直角坐标系,每一个像素点都对应一个坐标,这样就可以利用式(2)求出每一个平面几何图形Voronoi区域的重心.加权Voronoi区域一般是圆弧曲面,求曲面重心可利用积分法.同求普通Voronoi图的重心一样,用积分法是不太现实.由于加权Voronoi区域也是平面图形,所以公式(2)也适用于求加权Voronoi区域重心.

3.2 加权voronoi图区域重心实现过程

首先将生成元赋予不同的颜色,利用离散voronoi图的生成算法来生成每个生成元的Voronoi区域.对每一个生成元,从生成元点附近开始围绕生成元点以指定的颜色画点.权重大的向外扩展的填涂速度越快,相反,权重小的扩展速度较慢.当屏幕上所有的像素点都画上了颜色时则退出.这时不同颜色区域的边界即为加权Voronoi图的边,这条边一般是圆弧形的.在这个过程当中,画点的同时把每个颜色与该点相同的点的坐标记录下来进行累加,得到同一个区域的所有点的横纵坐标的累加值yi并且累加的个数即为n,这样将它们带入式(2)就可以得到这个Voronoi区域的重心.每一个生成元的Voronoi区域都用这种方法就可以得到每一个Voronoi区域的重心.由于在计算机中实现该算法时计算机中数据的存储空间是有限的,根据公式(2)计算重心坐标需要累加,如果结果太大可能会造成数据溢出所以对公式(2)进行变形为公式(3).

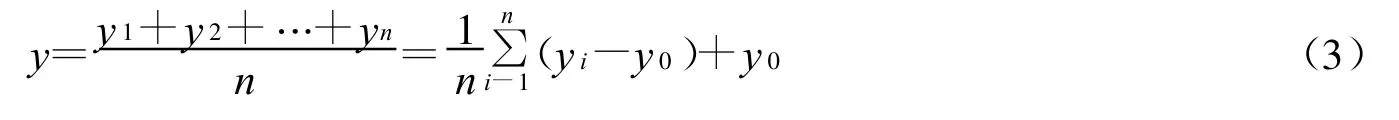
3.3 加权voronoi区域重心的意义

在日常的工作和生活中常常会遇到这样的情况:一些服务性的单位为了进一步发展或者是为了方便用户而需要设立新的服务网点;为了迎合城市建设和发展的整体规划,需要在某些位置上做出调整.对于此类问题,如以收费网点位置的调整为例,可以先根据初步的考察决定各网点的大概位置,然后以它们为生成元做出Voronoi图.一般我们会认为一个平面图形的重心是这个平面图形的平衡位置.通常认为公共设施的选址越接近平面图形的重心则它的选址越趋近合理.所以我们利用离散方法及公式3形成了图4.图中*位置即为每个加权voronoi区域的重心.

我们观察每个Voronoi区域的重心与它所对应的生成元的位置关系,如果二者距离比较远,则说明该生成元的位置有待调整.重心是使区域达到平衡的位置,使生成元适当地接近重心则在实际生活中更具合理性,而且经过这样的调整后的生成元分布更加均匀.在城市规划中就可以在建设营业厅时把假设的选址位置加以调整.选择在重心位置建设该营业厅.这个位置是最佳的选址地点.

4 结束语

在具体应用当中,比如,城市规划问题,各商场、医院、政府部门等重要场所的设置,可以把这些场所设为生成元.确定影响因素并进行评分后利用层次分析法得到不同的权值,从而再利用离散方法生成加权Voronoi图.利用加权Voronoi图的重心来分析各场所的选址位置.这样就给城市规划部门一个比较准确并且合理的选址建议.避免发生人群分布不均、拥挤等现象的发生.在建设这些场所时尽量接近重心位置这样使得设施分布更均匀合理.这些实际问题都可以用Voronoi图来解决.

总之,随着计算机技术的发展以及Voronoi图理论自身的不断成熟,展望未来,它必将在社会各个领域得到更广泛的应用.采用本文方法确定的选址地点,不仅可以综合考虑来自自然、社会、场所自身等影响因素,而且运用加权Voronoi图方法还能考虑场所之间的空间临近关系,直观地反映了各个场所的覆盖范围.为城市规划和新增场所选址以及空间布局等提供科学简便的方法.

[1]周培德,卢开澄.计算几何——算法分析与设计.北京:清华大学出版社,广西科学技术出版社.2000

[2]赵晔,张有会等.关于一般图形Voronoi图的离散构造法的研究.计算机应用与软件.2004,6

[3]许树柏.层次分析法原理.天津:天津出版社,1998

[4]G.Voronoi,Nouvelles applications des paramè ters continus à la théorie des formes quadratiques.Premier Mémoire: Sur quelques Proprieteés des formes quadratiques positives parfaits,J.Reine Angew,M ath,1988

[5]G.Voronoi,Nouvelles applications des paramè ters continus à la théorie des formes quadratiques.Deuxiè me Mémoire: Recherches sur les parallélloèdres primitives,J.Reine Angew.Math,1983

[6]陈军.Voronoi动态空间数据模型.北京:测绘出版社.2002