弹性粒子群优化算法及其在水电优化调度中的应用
陈烨兴,罗云霞,周慕逊
(1.浙江大学建筑工程学院,浙江杭州 310058;2.浙江水利水电专科学校电气工程系,浙江杭州 310018; 3.台州学院物理与电子工程学院,浙江台州 317000)
粒子群优化算法(particle swarm optimization,PSO)源于对鸟类捕食行为的模拟.由于该算法概念简单、容易实现,并且优化性能良好,因此得到了广泛的研究和应用.与其他随机智能优化算法一样,粒子群优化算法也存在着早熟收敛、后期收敛速度较慢等问题.为此,人们进行了大量的研究,出现了许多改进的算法,如自适应粒子群优化算法、量子粒子群优化算法、基于模拟退火的粒子群优化算法、基于组织进化的粒子群优化算法、文化粒子群优化算法、免疫粒子群优化算法、育种粒子群优化算法等,并将其应用于水电优化调度问题[1-10],但目前还没有形成比较通用的有效的改进算法[11].本文设计了一种弹性粒子群优化算法(resilient particle swarm optimization,RPSO),改变速度更新方程并引入惯性权重的自适应机制[1],将其应用于水电优化调度问题,并通过实例仿真进行性能比较和参数测试,验证了算法的可行性和有效性.
1 弹性粒子群优化算法
弹性粒子群优化算法[12]和粒子群优化算法的不同在于粒子的速度更新方程.假设在N维搜索空间中,有m个粒子,粒子i的位置表示为,第k次迭代时的位置表示为;粒子i的飞行速度表示为,第k次迭代时的速度表示为;粒子i的最优个体位置表示为,粒子群的全局最优位置表示为 Xg=(xg1,…,xgn,…,xgN).弹性粒子群优化算法的粒子速度更新方程为


式中:k——迭代代数;ω——自适应惯性权重因子;c1,c2——学习因子;r——(0,1)之间的随机数; sgn(◦)——符号函数——弹性修正值.
通过判断粒子的飞行方向取不同的弹性修正值:当粒子前后两次飞行方向一致时,说明该粒子从极值的一侧向其逼近,应加大修正值,以加快算法收敛;当粒子前后两次飞行方向不一致时,说明该粒子正在极值附近徘徊,应降低修正值,以免徘徊过久;若是其他情况,则不改变修正值.令

弹性修正值为

式中:η+——递增因子;η-——递减因子;两者满足0<η-<1<η+.
粒子的位置更新方程为

弹性粒子群优化算法由于引入了粒子对方向的判断和速度弹性值的设置,保证各粒子朝最优粒子飞行,而且当它与最优粒子很接近时,仍能保持一定的飞行速度,避免算法早熟收敛.
2 水电优化调度数学模型
设以发电量最大为优化调度目标,调度周期分为T个时段,以t代表时段变量,t=1,2,…,T;以Qt表示水库在t时段的发电引用流量;Ht表示水库在t时段的平均发电水头;Vt表示水库在t时段的平均库容,则优化调度目标函数为

约束条件为:
式中:A——系数,包括发电效率和时段时间的影响;Qmax,Qmin——允许的最大、最小发电引用流量;Vmax,Vmin——允许的最大、最小库容;Qrt——t时段的入库流量;ΔVqt——t时段的弃水总量;Nmax,Nmin——电站允许的出力上、下限.
3 弹性粒子群优化算法求解模型流程
弹性粒子群优化算法求解上述水电优化调度问题模型的流程设计如下:
步骤1:设计粒子编码,初始化粒子群,设置初始位置、初始速度及其边界,设置算法终止条件.设以发电引用流量Q为决策变量,则本问题解为T个时段的发电引用流量组合.将问题解对应于粒子位置,则粒子i位置表示为Xi=(Qi1,…,Qit,…,QiT),速度为Vi=(vi1,…,vit,…,viT).设群体规模为n,粒子在[Qmin,Qmax]之间随机产生n个粒子初始位置.初始速度设为V=(0,0,…,0).粒子位置及飞行速度的边界可根据实际问题确定.
步骤2:设计粒子适应度函数,计算各粒子的适应度值.粒子的适应度函数与本问题的目标函数和约束条件相关联,设粒子i的适应度为Fi,则

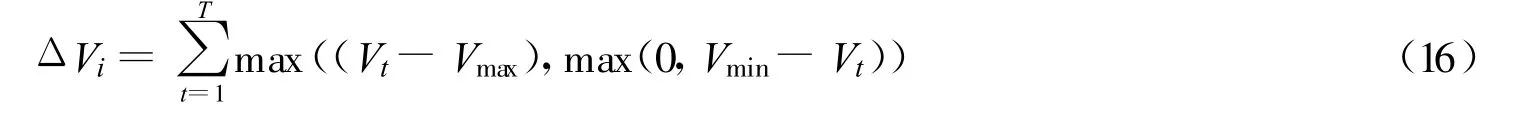
式中:A——保证适应度值为正的正整数;k1,k2——惩罚系数;ΔQ,ΔV——发电引用流量和库容的超限幅值.不满足约束条件时,ΔQ,ΔV不为零,粒子的适应度下降,对应解不可能成为最优解.
步骤6:按式(1)修正粒子的飞行速度,并将其限定在允许的范围内;按式(8)修正粒子的位置,并将其限定在允许范围内;按式(14)计算粒子的适应度;更新个体极值和全局极值.
步骤7:判断,若算法满足终止条件,则停止;否则,跳至步骤4.
4 实例仿真测试
某年调节水库有效库容3026万m3,正常蓄水位340.00m,死水位305.00m,下游水位设为常数174.00m,多年平均入库流量10.84m3/s.电站装机容量44MW,全部机组过水能力QG=30.0m3/s.调度期初水库水位为死水位;调度周期为1a,时段数T=12;采用多年平均入库径流;发电效率取η=0.80;发电引用流量范围为[Qmin,Qmax]=[3m3/s,30 m3/s],其中最小值考虑了下游最小保留流量.弹性粒子群优化算法参数设置[1,12]:粒子数n=20;自适应惯性权重因子ω变化范围[0.4,0.9];学习因子c1=c2=2;最大迭代次数500;弹性修正值上下限值为Δmax=0.5(Qmax-Qmin),Δmin=0.001(Qmax-Qmin),初始值和的取值范围为(0.01~0.1)(Qmax-Qmin);递增递减因子取η+=1.1,η-=0.5.
按照上述弹性粒子群优化算法求解步骤和方法,用Matlab仿真,得到各时段发电引用流量等仿真结果如表1所示,各时段的弃水量均为零.为了验证弹性粒子群优化算法的性能,分别采用弹性粒子群优化算法、自适应粒子群优化算法(APSO)[1]和基本粒子群优化算法进行Matlab仿真,比较各算法的最大粒子适应度值变化如图1所示.3种算法都具有一定的搜索能力,80代之后都处于收敛状态,但收敛效果相差很大,与基本粒子群优化算法和自适应粒子群优化算法相比,弹性粒子群优化算法找到局部最优点的次数明显增多.年总发电量比较为:基本粒子群优化算法13246万kW◦h,自适应粒子群优化算法13347万kW◦h,弹性粒子群优化算法13423万kW◦h.这表明弹性粒子群优化算法能有效地避免算法陷入局部最优.
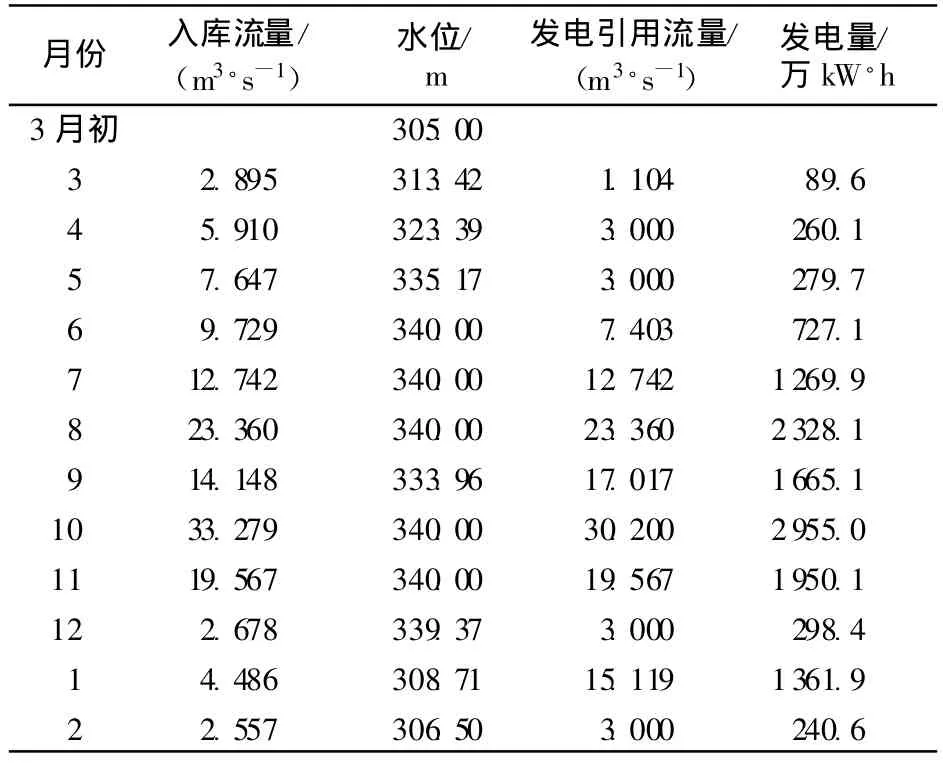
表1 弹性粒子群优化算法优化调度仿真结果Table 1 Simulated results of optimal scheduling by RPSO
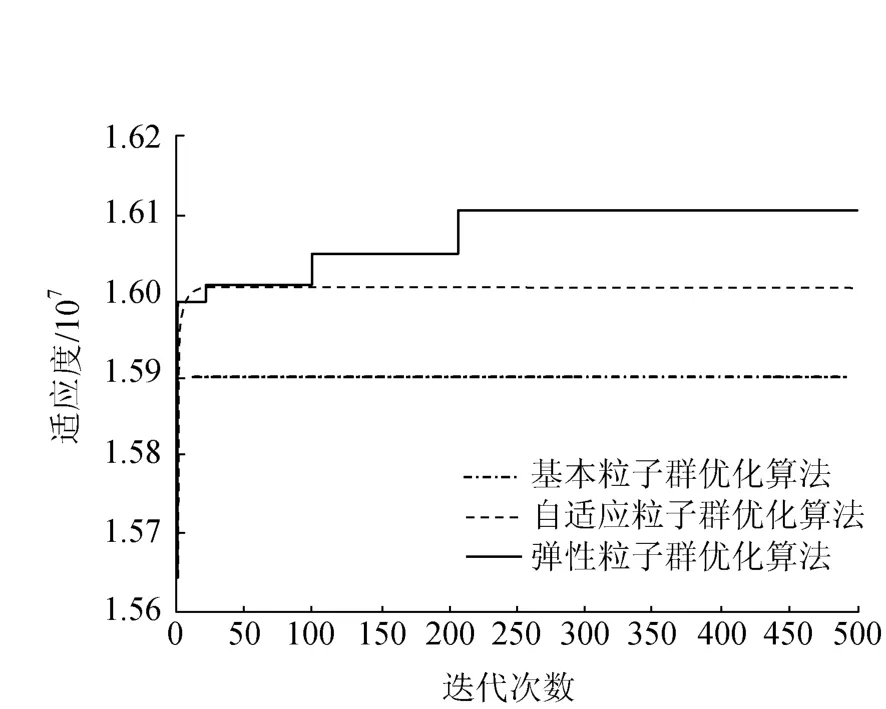
图1 最大粒子适应度变化曲线的比较Fig.1 Comparison among variation curves of the maximum fitness value
进一步测试递增因子η+和递减因子η-对弹性粒子群优化算法性能的影响:取 η+=1.2,1.1,1.0,η-=1.0,0.6,0.5,0.4,0,分析不同组合下算法的平均最优适应度值、成功率、平均计算时间和总发电量,仿真结果如表2所示.由表2分析可知,η+和 η-对弹性粒子群优化算法的性能有较大的影响,其中 η-比 η+对算法的影响要更强一些;η+和η-分别取1.0~1.1和0.5,算法收敛性能达到最佳.

表2 η+和η-对弹性粒子群优化算法性能影响测试Table 2 Calculated results for influences of η+and η-on performance of RPSO
5 结 语
弹性粒子群优化算法采用了一种弹性自适应的速度更新方程,当前粒子即使和最优粒子很接近,也能保持一定的飞行速度,从而避免了基本粒子群优化算法存在的后期进化速度慢、精度不高等问题.将弹性粒子群优化算法应用于求解以发电量最大为优化调度目标的水电优化调度问题,实例仿真表明算法是有效的.通过比较基本粒子群优化算法、弹性粒子群优化算法和自适应粒子群优化算法的求解适应度值变化曲线,弹性粒子群优化算法具有更强的全局寻优能力.弹性粒子群优化算法中的递增因子η+和递减因子η-对性能有较大的影响,通过测试分析,可以得出其收敛性能最好的取值范围.该算法既原理简单、容易实现,又能收敛到更好的全局最优解,拓展了改进粒子群优化算法在水电优化调度中的应用.
[1]罗云霞,王万良,周慕逊.基于自适应粒子群算法的梯级小水电群优化调度研究[J].水力发电学报,2008,27(4):7-11. (LUO Yun-xia,WANG Wan-liang,ZHOU Mu-xun.Research of optimum operationbased onAPSO for cascaded small hydropower stations [J].Journal of Hydroelectric Engineering,2008,27(4):7-11.(in Chinese))
[2]陈立华,梅亚东,杨娜.自适应多策略粒子群算法在水库群优化调度中的应用[J].水力发电学报,2010,29(2):139-144. (CHEN Li-hua,MEI Ya-dong,YANG Na.Adaptive multi-variant strategy particle swarm optimization algorithm and its application to the optimal operation of cascade reservoirs[J].Journal of Hydroelectric Engineering,2010,29(2):139-144.(in Chinese))
[3]周慕逊,王正初,罗云霞,等.基于MAPSO算法的水库优化调度与仿真[J].计算机工程,2008,34(12):189-191.(ZHOU Muxun,WANG Zheng-chu,LUO Yun-xia.Reservoir operation optimization and simulation based on modified adaptive particle swarm optimization[J].Computer Engineering,2008,34(12):189-191.(in Chinese))
[4]张智晟,董存,吴新振.基于量子粒子群优化算法的水电系统经济运行[J].电网技术,2009,33(18):68-72.(ZHANG Zhisheng,DONG Cun,WU Xin-zhen.Economic operation of hydropower system based on quantum particle swarm optimization algorithm[J]. Power System Technology,2009,33(18):68-72.(in Chinese))
[5]申建建,程春田,廖胜利,等.基于模拟退火的粒子群算法在水电站水库优化调度中的应用[J].水力发电学报,2009,28 (3):10-15.(SHEN Jian-jian,CHENG Chun-tian,LIAO Sheng-li,et al.Optimization of hydropower station operation by using particle swarm algorithm based on simulated annealing[J].Journal of Hydroelectric Engineering,2009,28(3):10-15.(in Chinese))
[6]马玉新,解建仓,罗军刚.基于组织进化粒子群算法的水电站水库优化调度研究[J].西安理工大学学报,2009(3):256-262. (MA Yu-xin,XIE Jian-cang,LUO Jun-gang.Study onoptimum operationbased onorganizational evolutionary particle swarm algorithm for hydropower station reservoir[J].Journal of Xi'an University of Technology,2009(3):256-262.(in Chinese))
[7]何玲丽,周建中,卢有麟,等.基于文化粒子群算法的梯级水电站优化调度研究[J].水电能源科学,2009,27(1):164-168. (HE Ling-li,ZHOU Jian-zhong,LU You-lin,et al.Optimal dispatching of cascaded hydropower stations based on cultural particle swam optimization algorithm[J].Water Resources and Power,2009,27(1):164-168.(in Chinese))
[8]李安强,王丽萍,蔺伟民,等.免疫粒子群算法在梯级电站短期优化调度中的应用[J].水利学报,2008,39(4):426-432.(LI An-qiang,WANG Li-ping,LIN Wei-min,et al.Application of immune particle swarm optimization algorithm to short-term optimal dispatch of cascade hydropower stations[J].Journal of Hydraulic Engineering,2008,39(4):426-432.(in Chinese))
[9]向波,纪昌明,罗庆松.免疫粒子群算法及其在水库优化调度中的应用[J].河海大学学报:自然科学版,2008,36(2):198-202.(XIANG Bo,JI Chang-ming,LUO Qing-song.Immune particle swarm optimization algorithm and its application in reservoir operation optimization[J].Journal of Hohai University:Natural Sciences,2008,36(2):198-202.(in Chinese))
[10]杨道辉,马光文,杨梅.育种粒子群算法在梯级水电站优化调度中的应用[J].水力发电学报,2010,29(2):207-212(YANG Dao-hui,MA Guang-wen,YANG Mei.Application of BBPSO to optimal operation of cascade hydropower stations[J].Journal of Hydroelectric Engineering,2010,29(2):207-212.(in Chinese))
[11]董前进,曹广晶,王先甲,等.粒子群优化算法在水文科学中的应用进展[J].中国工程科学,2010,12(1):80-84.(DONG Qian-jin,CAO Guang-jing,WANG Xian-jia.et al.Application prospect of PSO in hydrology[J].Engineering Sciences,2010,12(1):80-84.(in Chinese))
[12]李勇刚,桂卫华,阳春华,等.一种弹性粒子群优化算法[J].控制与决策,2008,23(1):95-99.(LI Yong-gang,GUI Wei-hua,YANG Chun-hua,et al.A resilient particle swarm optimization algorithm[J].Control and Decision,2008,23(1):95-99.(in Chinese))

