大型输水渠道运行仿真系统控制周期选取

丁志良，余启辉，杨哲江

(长江勘测规划设计研究院，湖北武汉 430010)

渠道运行控制的目标是提高渠系的全面调度运行水平，改善输水效率，实现适时、适量地供水，避免供水的不足与浪费，降低调度运行费用，从而达到提高水资源利用率的目的[1].为实现对渠道水位和流量的控制，渠道系统中应设置足够数量的节制闸，渠道控制主要是通过对一系列节制闸的启闭控制来达到控制渠道中水流的目的.渠道运行自动化控制系统本质上就是一连串的控制闸门的开启与整个渠道水量、水深之间动态变化的关系，是系统从一个状态到达另一个状态平稳过渡并保持稳定的过程.

闸门的运行控制，一般要求有确定的闸门运动变量.如果单位时间内闸门启闭次数较多，对控制精度要求较高，则变速运行的优越性就非常突出，通过开环或闭环控制模式调节流量时，闸门的变速运行将使系统的运行更为灵活，对于较大的渠道系统，当采用PID环路控制方法时，应优先考虑变速度控制.大型输水渠道系统中，变速闸门的运行速度范围为0～0.5m/min，通过对南水北调中线工程规模的渠道进行仿真计算，发现当闸门变速运行时，闸门调节速度的限制对系统的动态响应没有影响[2-3].控制周期是指闸门控制器给出闸门开度控制信号的时间间隔，闸门变速运行时，模拟计算中闸门开度是在每一个控制周期末以一定的速度很快调节到计算值，所以，模型控制周期的选取对系统动态响应有较大的影响，控制周期的选择应根据渠段的水力特性来确定.本文对渠道等体积及下游常水位运行方式下控制周期变化时，影响渠道系统动态响应的因素进行了仿真分析，在此基础上，研究了仿真系统控制周期的合理取值问题.

1 渠道系统运行控制数学模型

1.1 渠道控制系统水力学模型

渠系的动态过程可以用拟线性双曲型偏微分圣维南方程组结合非线性断面结构方程来模拟.圣维南方程组形式如下[4-5]:

式中:B——水面宽，m;Z——水位，m;t——时间，s;Q——流量，m3/s;C——谢才系数;s——断面的距离坐标，m;g——重力加速度，m/s2;A——过水断面面积，m2;q——旁侧入流量，m3◦s-1/m;v——水流沿轴线方向的流速，m/s;vqs——旁侧入流在水流方向的平均流速(常忽略不计)，m/s;R——水力半径，m;i——渠道底坡; M——明渠单宽、定深(常深)断面沿程的放宽率对于棱柱型明槽，可令M=0或.

求解圣维南方程组的数值方法中普莱士曼(Preissmann)隐式差分格式以精度高、无条件收敛等优点被广泛采用，通常采用追赶法求解[6-7].

1.2 渠道控制系统仿真模型

渠系控制系统根据来自渠道中的信息，通过一定的方式计算控制设备的调整量，控制渠道的某一或某些变量按一定的规则变化，以实现预定的控制目标.渠道自动控制既要考虑水流的运动特性，又要考虑控制理论在此基础上的应用.

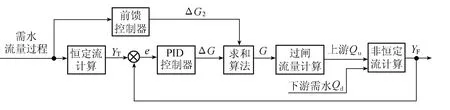
图1 渠道自动化控制系统Fig.1 Automatic control system for canals

目前所编写的渠道控制仿真程序可以完成多渠段、多取水口，包含倒虹吸、渡槽等建筑物的渠道系统在采用不同控制器条件下的渠道运行控制仿真过程.仿真模型采用流量前馈+水位反馈的PID控制器[8-9]，仿真系统控制流程图如图1所示，图中符号含义见文献[9].渠道控制仿真模型主要包括6个功能模块:输入模块、恒定流计算模块、非恒定流计算模块、控制器算法模块、过闸流量计算模块、输出模块，这6个模块紧密联系，相互作用，以实现渠段按所设计的运行方式运行，满足下游的需水要求[10-11].

2 控制周期选取与系统动态响应

闸门变速运行时，闸门运行受到控制周期、控制周期内闸门最大(最小)增量值、死区的影响.在本文的研究中，闸门调节速度的上限完全可以满足各控制周期内闸门最大增量值的要求，而闸门的最小增量值可以通过设置闸门死区来代替.死区的设置对系统的动态响应及控制操作的影响可参考文献[10]，本文为了排除死区设置的影响，主要研究无死区设置情况下，系统控制周期的选取问题.

为了排除太多渠段串联时对结果产生影响，以及为了实现系统的快速稳定，选取南水北调工程应急供水段中的前3个渠段作为模拟对象.模拟渠段的起点为古运河节制闸，终点为沙河(北)节制闸，全长约为47km，整个模拟渠道系统由节制闸分成3个渠段，起、终点渠段设计流量分别为170m3/s和165m3/s，沿程包括2个分水口和3个倒虹吸，暗渠、桥梁、排水建筑物若干.模拟渠道的详细参数见文献[2].

模拟计算中，采用分水口及渠道下游端流量减少及增加2个不同工况.工况一:永安分水口(位于第二渠段)及渠道下游流量在1～3h内由70%设计流量直线减少到50%设计流量;工况二:永安分水口及渠道下游流量在1～3h内由50%设计流量直线增加到70%设计流量.其余分水口流量为零并保持不变.

2.1 渠道等体积运行计算结果及分析

仿真计算发现，控制周期变化时，PID参数中比例系数Kp对系统的动态响应影响很大，且呈现一定的规律，而积分系数Ki、微分系数Kd的影响较小，可保持一较为理想的定值不变.

通过对控制周期增加时，Kp，Ki，Kd不变的情况进行一系列模拟，发现随着控制周期的增大，系统的波动次数增多，波幅增大，稳定时间变得很长，而增加Kp值可以很明显地改善系统的动态响应及控制性能.分析其原因，主要是控制周期增大后，每一个控制周期PID控制器的输出增量也增加，这时需要较大的Kp才能达到系统的控制输出，以加快系统的响应速度.通过PID参数寻优及试算，渠道等体积运行时，Kp与控制周期 T有如图2所示的关系，Kp按照此规律变化，系统的动态响应及动态性能都较好.取Ki=0.2，Kd=0.

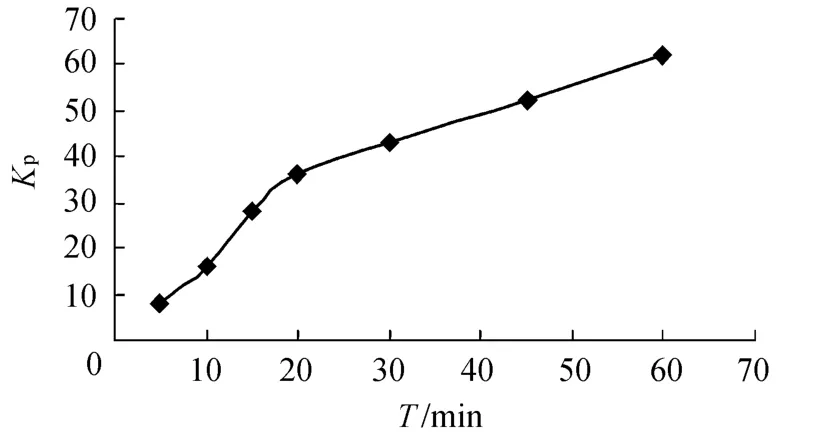
图2 等体积运行Kp与T变化关系Fig.2 Relationship between Kpand T under constant volume operation method

渠道等体积运行时控制性能指标见表1(性能指标的定义见文献[12]，指标统计时先各渠段单独计算，然后求所有渠段的最大值及平均值);各渠段响应时间如图3所示;渠段1～3最大水位降幅变化规律一致，其中渠段1最大水位降幅如图4所示.

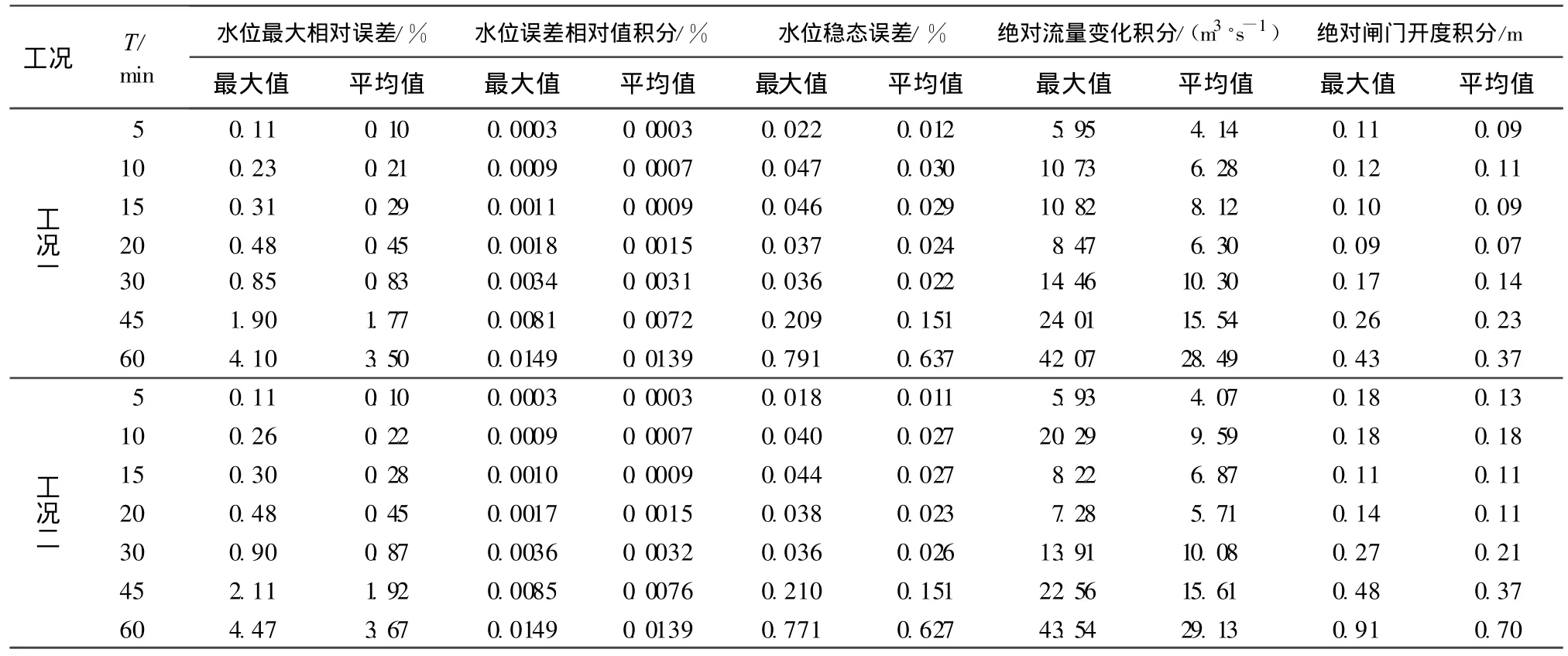
表1 等体积运行渠道控制性能指标Table 1 Control performance indices for constant volume operation method

由表1及图3和图4的计算结果，可以得到以下结论:

a.在等体积运行方式下，水位指标基本都随着控制周期的增加而增大，表明控制周期越大，系统对水位的控制效果越差，渠道水位的波动幅度越大，波动时间越长.而且水位指标值在控制周期T≤30min时增加的较慢，在T＞30 min时增加的较快，所以当 T≤30min时，系统对水位的控制效果都较为良好.2种工况下，辅助性能指标绝对流量变化积分(IAQ)及绝对闸门开度积分(IAW)都随控制周期的增加先增大后减小再持续增大，并且绝对闸门开度积分在T=15～20min时达到最小值，绝对流量变化积除了T=5min外，也是在T=15～20min时达到最小值，所以单从系统运行过程中闸门流量及闸门开度稳定过程考虑，取T=15～20min较为理想.

b.等体积运行时，相同流量变幅及变化速率下，渠道流量增加时水位降速一般都大于相应的流量减少情况.这是因为流量增加时，各渠段最大水位降速都发生在渠段下游端，而本文模拟的3个渠段中，下游端都布置有倒虹吸，倒虹吸管水头损失与其流量平方成正比[2]，当流量增加时，倒虹吸水头损失增加的更快，致使流量增加时，各渠段最下游端水位降落得很快.就某一特定工程中流量增加或减少的不同情况而言，同一流量变幅下，当流量减少时，渠道的流量变速可以取得较大些，或同一流量变速下，当流量减少时，渠道的流量变幅可以取得较大些.

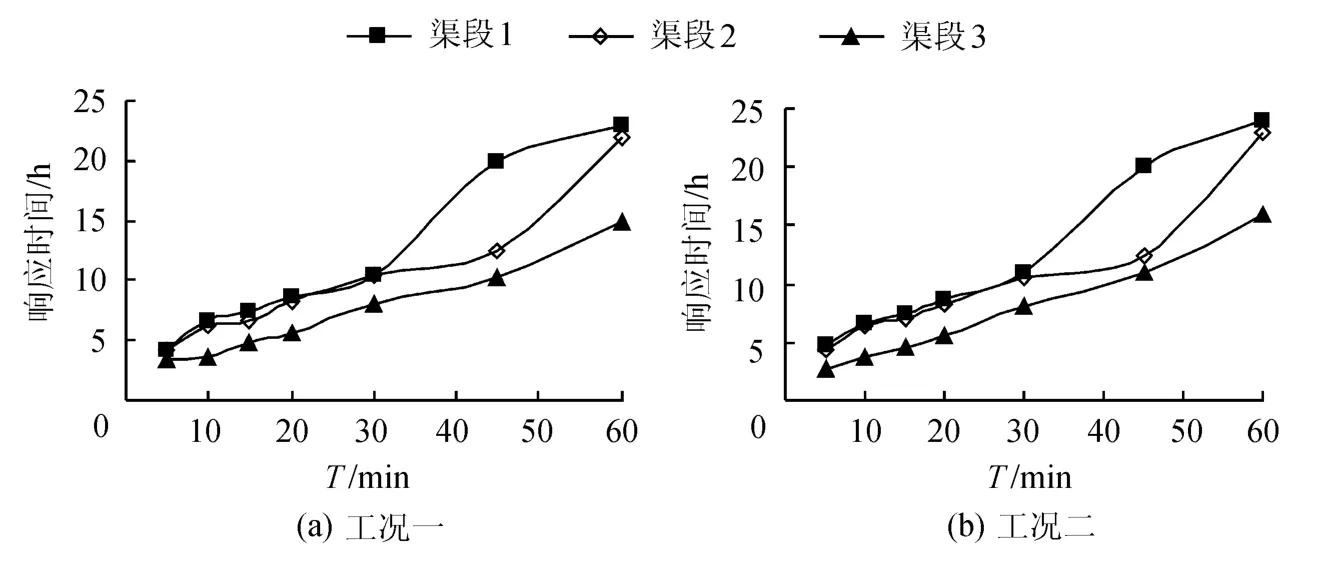
图3 等体积运行各渠段响应时间Fig.3 Response time of various canals under constant volume operation method

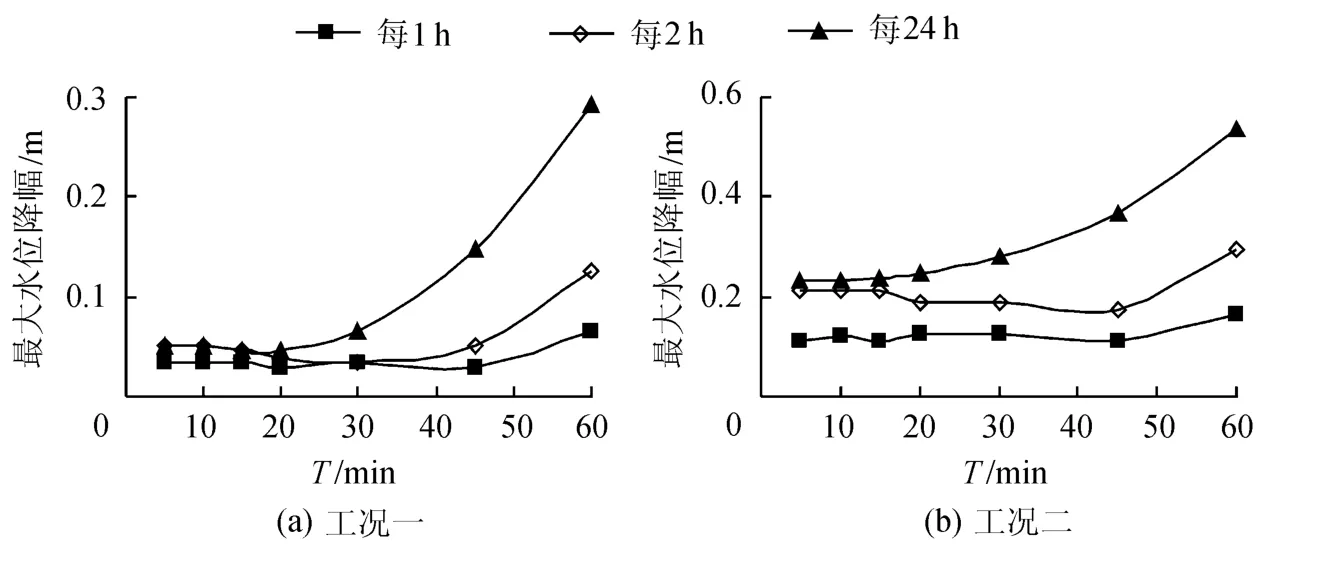
图4 等体积运行渠段1最大水位降幅Fig.4 Decrease amplitude of maximum water level of canal pool 1 under constant volume operation method

c.等体积运行时，随着统计水位降落时间的增长，水位降幅受控制周期的影响也越大，这主要是因为控制周期越大时，水位的波动幅度越大，而最大波幅的波动时间也越长，所以统计水位降幅的时间越长，越能反映水位的最大降落值，因而其受控制周期的影响也越大.就本文模拟的工况，当控制周期T≤30min时，每1h，2h及24h的水位降幅随控制周期的变化都不大.

d.各渠段的响应时间随控制周期的增大而增长，且2种工况下，各渠段的响应时间随控制周期的变化基本相同，两者相差很小.往渠道上游方向，渠段的稳定时间有所增长.当控制周期T≤30min时，3个渠段的响应时间随控制周期的变化近似成直线增加，且响应时间都较短.所以，从缩短渠道稳定时间及避免闸门电动机频繁启动方面考虑，可选择T=15～30min作为闸门控制输出周期.

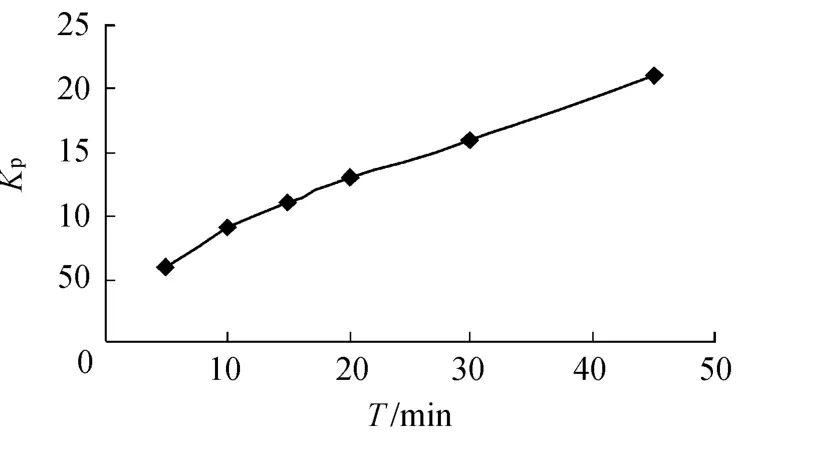
图5 下游常水位运行Kp与T变化关系Fig.5 Relationship between Kpand T under constant downstream depth operation method

2.2 渠道下游常水位运行计算结果及分析

渠道下游常水位运行时，比例系数Kp与控制周期T有如图5所示的关系，Kp按照此规律变化，系统的动态响应及动态性能都较好.取Ki=0.04，Kd=0.

渠道下游常水位运行时控制性能指标见表2;各渠段响应时间如图6所示;渠段1～3最大水位降幅变化规律一致，其中渠段1最大水位降幅如图7所示.

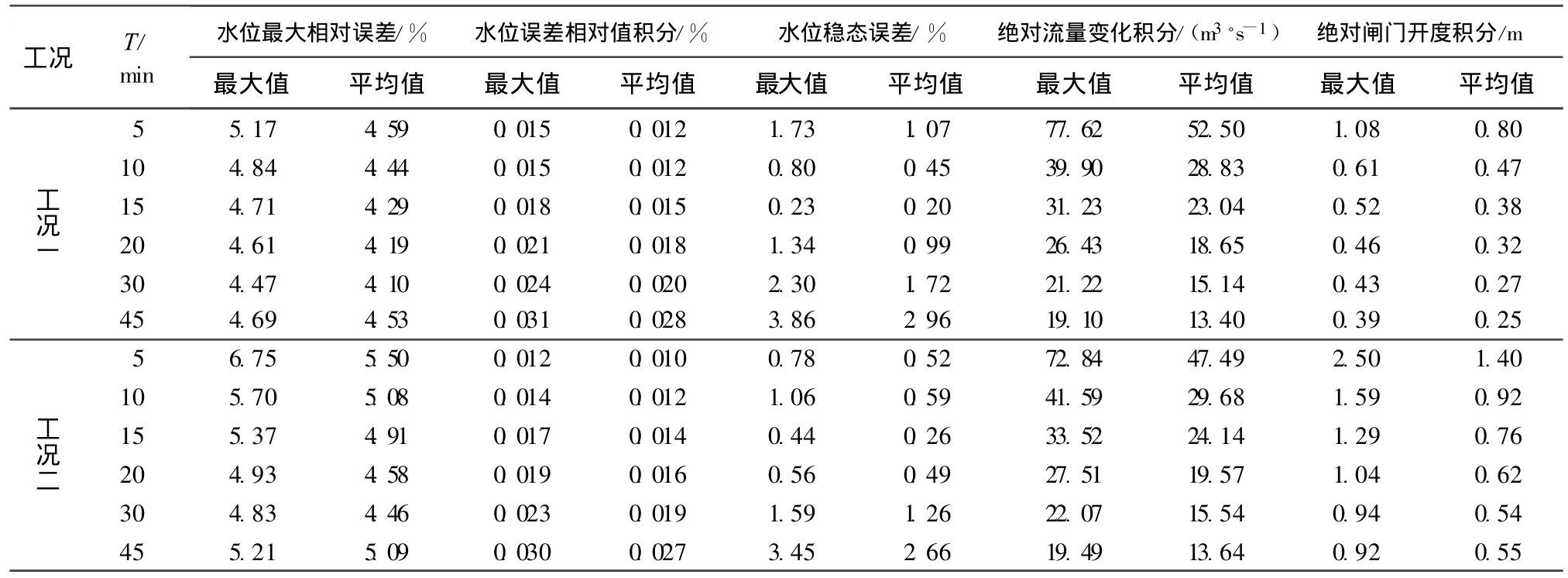
表2 下游常水位运行渠道控制性能指标Table 2 Control performance indices for constant downstream depth operation method

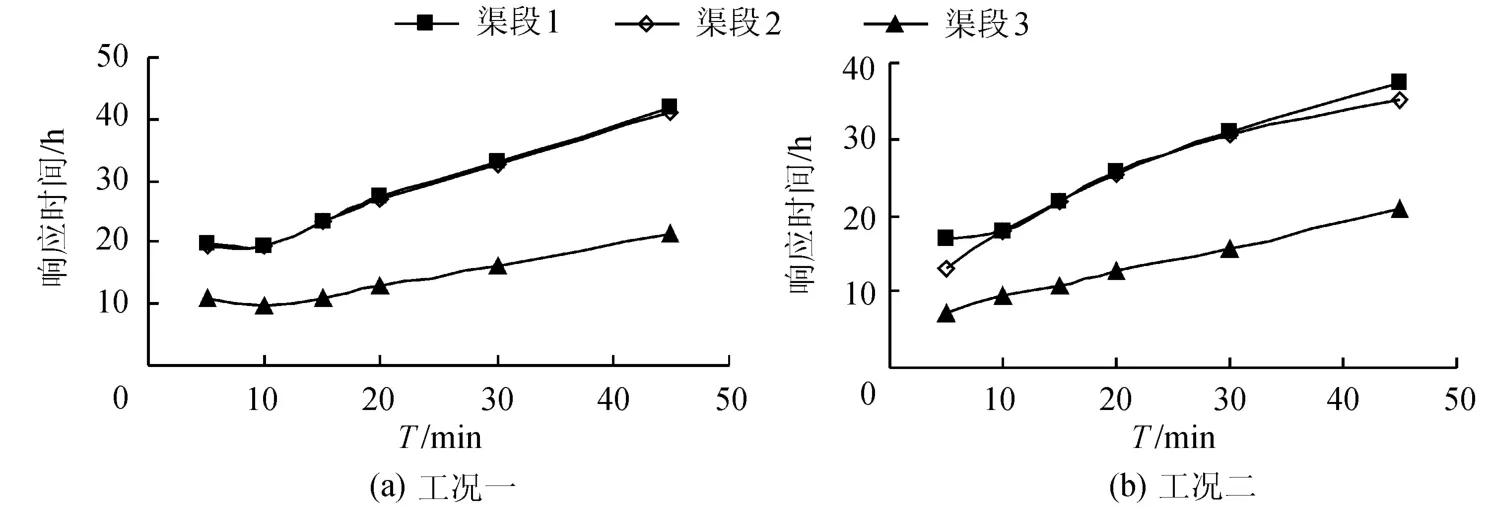
图6 下游常水位运行各渠段响应时间Fig.6 Response time of various canals under constant downstream depth operation method

由表2及图6和图7的计算结果，可以得出以下结论:

a.下游常水位运行方式下，水位指标中水位最大相对误差(MAE)、水位稳态误差(StE)基本都随控制周期的增加先减小后增大，水位误差相对值积分(IAE)随控制周期的增加而持续增加，但总体而言，在控制周期T≤30min时，水位指标的变化都较小.辅助性能指标绝对流量变化积分(IAQ)及绝对闸门开度积分(IAW)都随着控制周期的增加而持续减小，说明控制周期越大，系统运行过程中闸门流量和开度的稳定过程越好，其原因是当下游常水位运行与下游运行概念结合时，会显示出一定的缺点，因为渠段蓄水量必须按与自然趋势相反的方向改变，为了达到需求的蓄水量变化，渠段上游末端的入流变化必须要超量补偿出流变化，当控制周期较小时，为了跟踪下游目标水位，各渠段上游进行频繁超调，从而引起过闸流量和开度的超调都较大，而控制周期增大后，减小了闸门开度及流量的超调.

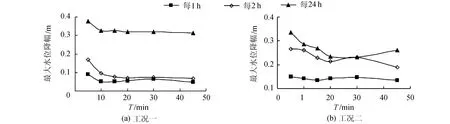
图7 下游常水位运行渠段1最大水位降幅Fig.7 Decrease amplitude of maximum water level of canal pool 1 under constant downstream depth operation method

b.下游常水位运行方式下，相同流量变幅及变化速率下，渠道流量增加时每1h和2h的最大水位降幅都大于相应流量减少情况，而每24h的最大水位降幅都小于相应流量减少情况，这是由于渠道流量增加时，各渠段下游端开闸引起的落水波使得下游端水位短时间内偏离目标水位而快速降低，致使短时间内最大水位降幅相对较大，而为了跟踪目标水位上游节制闸又进行调节，使得一段时间后下游端水位又向目标水位恢复，所以相对而言，长时间统计的最大水位降幅并不大.

c.下游常水位运行各统计时段内最大水位降幅基本都比相应情况的等体积运行方式大，特别是在流量减少情况时.在该运行方式下，各渠段统计时段内最大水位降幅受控制周期的影响并不明显，所以只要合理地选择PID控制器中的Kp，控制周期的增加并不会带来水位降速的增加.若采用等体积运行中相同的水位降速限制标准，则在模拟的控制周期范围内，各统计时段的最大水位降幅都满足限制标准的要求.

d.下游常水位运行方式下，各渠段响应时间基本都随着控制周期的增加而增长，且都远大于相同情况的等体积运行方式.2种工况下，渠段1和2的响应时间基本相同，并都大于渠段3，这是因为在整个渠道系统过渡过程中，最下游渠段最先稳定，然后依次向上游逐渐稳定，而渠段1和2稳定时间相差不大的原因是，渠段1比渠段2短得多，相比之下缩短了稳定时间.相同情况下，渠道流量减少比流量增加时渠段的响应时间稍长.若从缩短渠道稳定时间及避免闸门电动机频繁启动方面考虑，可选择T=15～30min作为闸门控制输出周期.

e.根据文献[13]，对于下游反馈控制器，其控制周期应根据渠段的水力特性进行选择.当回水影响渠段部分长度时，系统的响应被考虑为一阶，当回水影响渠段整个长度时，系统的响应被考虑为二阶.对于一阶系统，设置PID控制器的一个经验规则是采用控制周期近似在1/3～4/5的波传播时间(滞后时间)之间，而对于二阶系统，采用控制周期近似在20%～60%波动周期之间.对于本文的算例而言，根据这种规则，则渠段1，2，3的控制周期T分别为11～28min，20～53min，21～52min.由于目前使用的程序需要对所有渠段采用相同的控制周期，所以可采用T=20～30min，与本文模拟给出的合理取值范围基本一致.

3 结 语

鉴于大型输水渠道运行调度的复杂性，在工程建设前，对输水运行调度问题进行相关技术研究是不可或缺的，在设计时利用数学模型对各种可能出现的工况进行预演，优化设计参数，改进整体设计，为工程建成后进行实时运行调度提供服务.大型输水渠道自动化运行控制仿真计算中，闸门控制器输出周期的选取对系统动态响应的影响较大.当控制周期增大时，通过合理地增加PID控制器中的比例系数Kp，不但可以明显地减少闸门的启闭，而且对系统动态响应及控制性能的影响又较小.通过对给定算例进行模拟计算，给出了渠道等体积及下游常水位运行时Kp随控制周期T的变化关系，当系统控制周期改变后，可以把Kp作为唯一可调参数并利用Kp与 T的关系来指导系统调节.通过对计算结果进行进一步的比较和分析，在渠道等体积及下游常水位运行方式下，都可选择闸门控制输出周期T=15～30min.

[1]BUYALSKI CP，EHLER D G，FALVEY H T，et al.Canal systems automationmanual volumeⅠandⅡ[M].Denver Colo:US Bureauof Reclamation，1991.

[2]丁志良.长距离输水渠道水力特性及运行控制研究[D].武汉:武汉大学，2009.

[3]TAN Guang-ming，DING Zhi-liang，WANG Chang-de，et al.Gate regulation speed and transition process of unsteady flow in channel[J]. Journal of Hydrodynamics，2008，20(2):231-238.

[4]STRELKOFF T S，FALVEY H T.Numerical method used to model unsteady canal flow[J].Journal of Irrigation and Drainage Engineering，1993，119(4):637-655.

[5]TAN Guang-ming，DING Zhi-liang，WANG Chang-de，et al.Gate regulation speed and transition process of unsteady flow in channel[J]. Journal of Hydrodynamics，2008，20(2):231-238.

[6]LIU Fu-bo，FEYEN J，BERLAMONT J.Downstream control algorithm for irrigation canals[J].Journal of Irrigation and Drainage Engineering，1994，120(3):468-483.

[7]范杰，王长德，管光华，等.渠道非恒定流水力学响应研究[J].水科学进展，2006，17(1):55-60.(FAN Jie，WANG Chang-de，GUAN Guang-hua，et al.Study on the hydraulic reaction of unsteady flows in open channel[J].Advances in Water Science，2006，17(1): 55-60.(in Chinese))

[8]刘永，尚涛.基于模糊/PID控制的渠道运行系统设计和仿真[J].系统仿真学报，2008，20(7):1892-1895.(LIU Yong，SHANG Tao.Design and simulation of canal's moving system based on fuzzy/PID control[J].Journal of System Simulation，2008，20(7):1892-1895.(in Chinese))

[9]姚雄，王长德，丁志良，等.渠系流量主动补偿运行控制研究[J].四川大学学报:工程科学版，2008，40(5):38-44.(YAO Xiong，WANG Chang-de，DING Zhi-liang，et al.Study on canal system operation based on discharge active compensation[J].Journal of Sichuan University:Engineering Science Edition，2008，40(5):38-44.(in Chinese))

[10]DING Zhi-liang，WANG Chang-de，TAN Guang-ming，et al.Deadbands and the dynamic response and performance of large water transfer canal system[J].Journal of Northeast Agricultural University，2009，16(2):58-65.

[11]管光华，王长德.长渠系稳态恒定流解法与非恒定流解法差异及对控制方式的影响[J].南水北调与水利科技，2008，6(5): 13-17.(GUAN Guang-hua，WANG Chang-de.Difference study of steady flow and unsteady flow simulation for long canal system[J]. South-to-North Water Transfers andWater Science&Technology，2008，6(5):13-17.(in Chinese))

[12]CLEMMENS A J，KACEREK T F，GRAWITZ B，et al.Test case for canal control algorithms[J].Journal of Irrigation and Drainage Engineering，1998，124(1):23-30.

[13]CLEMMENS A J，SCHUURMANS J.Simple optimal downstream feedback canal controllers:theory[J].Journal of Irrigation and Drainage Engineering，2004，130(1):26-34.