基于MATLAB有限元法结构分析
黄 辉
(1.湖南省永州市交通局,湖南永州 425006; 2.中南大学土木建筑学院,湖南长沙 410075)
0 引言
目前在工程技术领域内常用的数值模拟方法包括有限单元法、边界单元法、离散单元法和有限元差分法等。但就实用性和应用的广泛性而言,主要还是有限单元法。MATLAB是当今国际科技领域内具有较大影响力及活力的软件。它起源于矩阵运算,并已经发展成一种高度集成的计算机语言。它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、便捷的与其他程序和语言接口的功能。工程人员通过自己编写的M函数文件或调用MATLAB提供的工具箱,可以高效求解较复杂的工程问题,并对系统进行动态仿真和数值计算结果的图形输出。
在一般的结构问题分析中,平面梁元(Beam Element)是使用较多的二维有限元之一。本文以平面梁元为例探讨有限元法在MATLAB中的应用。平面梁元的系数有弹性模量E、惯性矩I和长度L。每个梁元有2个节点,并且假定它是水平的。梁元有4个自由度——每个节点有2个自由度(横位移和转角)。约定位移向上为正,转角逆时针方向为正。对一个有n个节点的结构而言,其整体刚度矩阵K的维数为2 n×2 n。忽略轴向形变,单元刚度矩阵k给定如式(1)[1-3]。
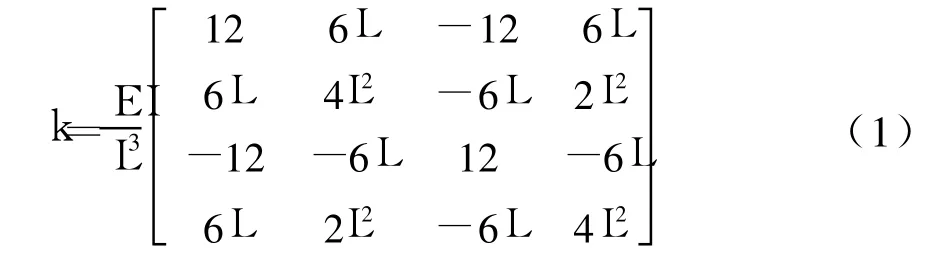
1 MATLAB有限元分析
1.1 运用MATLAB进行有限元方法解决实际问题的步骤[2]
运用MATLAB进行有限元方法解决实际问题的6个步骤简述如下:
1)离散化域:将一个表示结构或连续体的求解域离散为若干个不同的有限大小和形状的子域(单元),子域和子域之间通过节点进行连接(手动进行离散);
2)写出单元刚度矩阵:用MATLAB写出域内每个单元的单元刚度矩阵;
3)集成整体刚度矩阵:用MATLAB使用直接刚度法集成整体刚度矩阵;
4)引入边界条件:引入支座、外加荷载和位移等边界条件(手动进行实现);
5)求解方程:分解(手动进行)整体刚度矩阵并用高斯消去法(MATLAB)求解方程组;
6)后处理:根据求得的结构节点位移矢量,求解支反力、单元节点力和单元应力。
1.2 编写M函数文件
借助于MATLAB强大的编程功能,写出有关平面梁元结构的5个M函数文件:
1)BeamElementStiffness(E,I,L,)——该函数用于计算弹性模量E、转动惯量I、长度L的梁元的单元刚度矩阵。它返回4×4的单元刚度矩阵k。
2)BeamElementAssemble(K,k,i,j)——该函数将连接节点i和节点j的梁元的单元刚度矩阵k集成到整体刚度矩阵K。每集成一个单元,该函数都将返回2n×2n的整体刚度矩阵K。
3)BeamElementForces(k,u)——该函数用单元刚度矩阵k和单元节点位移矢量u计算单元节点力矢量。它返回4×1的单元节点力矢量f。
4)BeamElementShearDiagram(f,L)——该函数绘制节点力矢量为f和长度为L的单元剪力图。
5)BeamElementMomentDiagram(f,L)——该函数绘制节点力矢量为f和长度为L的单元弯矩曲线图。
在MATLAB软件集成环境中,使用上述5个M函数文件时,首先根据实际结构给出函数所需要用到的参数(E,I,L,K,k,i,j),然后可任意调用5个M函数文件中的一个进行计算。因本文重点不在讲述MATLAB软件的使用方法,如何在MATLAB集成环境中编写并使用M函数文件请参阅文献[4]。
2 实例分析
下面通过一个实例验证MATLAB的有限元求解全过程。如图1所示的连续梁[5],已知E=210GPa,I=50×10-6m4。求节点2、节点3和节点4的转角,并绘出单元的剪力图和弯矩图(计算单位取kN和m)。
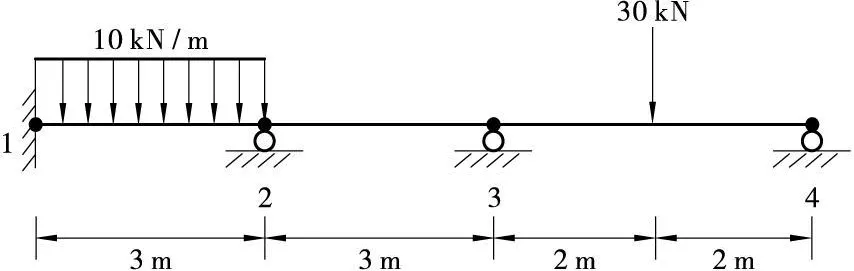
图1 三单元四节点连续梁
2.1 模型简化及计算
将结构划分为3个单元4个节点,单元①由节点1和节点2组成;单元②由节点2和节点3组成;单元③由节点3和节点4组成。首先,需要用等效节点荷载分别替代单元①和③的分布荷载和非节点集中荷载。然后根据M函数求出单元的刚度矩阵k1,k2,k3;该结构有4个节点,所以整体刚度矩阵是8×8的;由于有3个单元,故3次调用BeamElementAssemble()函数,求得整体刚度矩阵K。引入本题的边界条件后,分解(手动进行)整体刚度矩阵K并用高斯消去法(MATLAB)求解,最后解得节点2、3、4的转角分别是0.000 6、-0.001 2、0.002 0 rad(正号表示逆时针方向;负号表示顺时针方向)。
2.2 结果后处理
首先用MATLAB命令求出节点1、2、3、4的支反力和内力(剪力和弯矩)。建立结构的节点位移矢量U,然后计算结构的节点荷载矢量F。故节点1、2、3、4的垂直支反力分别是3.994 6、-8.478 3、7.724 7、-3.240 5 kN(正号表示方向向上;负号表示方向向下)。节点1、2、3、4的弯矩分别是3.994 6、7.5、-15、15 kN◦m(正号表示逆时针方向;负号表示顺时针方向)。很显然,满足力的平衡。
然后建立单元位移矢量u1、u2和u3,然后用BeamElementForces()函数求出单元矢量f1、f2和f3。需要注意的是,由于分布荷载和非节点集中荷载,所以需要对单元①和③的力进行修正。例如,修正后单元矢量f1为[18.994 6;11.494 6;11.005 4;0.489 1]。
最后调用BeamElementShearDicgram()和BeamElementMomentDicgram()函数分别绘出单元的剪力图和弯矩图。本文仅给出单元①的剪力图(图2)和弯矩图(图3)。
2.3 MATLAB实现过程(程序代码)
clear
E=210e6;
I=50e-6;
L1=3;
L2=3;
L3=4;
k1=BeamElementStiffness(E,I,L1);
k2=BeamElementStiffness(E,I,L2);
k3=BeamElementStiffness(E,I,L3);
K=zeros(8,8);
K=BeamAssemble(K,k1,1,2);
K=BeamAssemble(K,k2,2,3);
K=BeamAssemble(K,k3,3,4)
k=[K(4,4)K(4,6)K(4,8);K(6,4)K(6,6)K(6,8);K(8,4)K(8,6)K(8,8)]
f=[7.5;-15;15]
u=kf
U=[0;0;0;u(1);0;u(2);0;u(3)]
F=K*U
u1=[U(1);U(2);U(3);U(4)];
u2=[U(3);U(4);U(5);U(6)];
u3=[U(5);U(6);U(7);U(8)];
f1=BeamElementForces(k1,u1);
f1=f1-[-15;-7.5;-15;7.5]
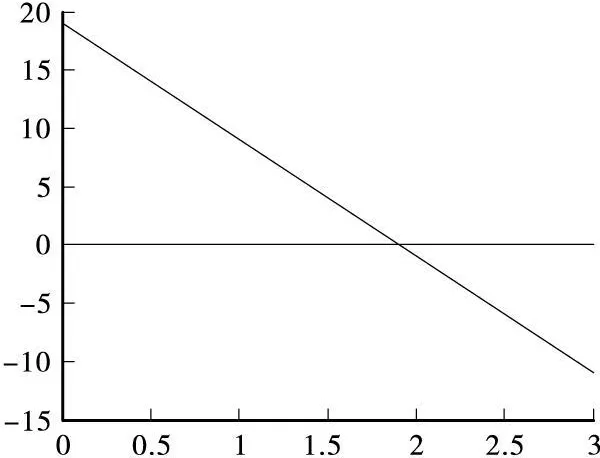
图2 单元①的剪力图(kN)
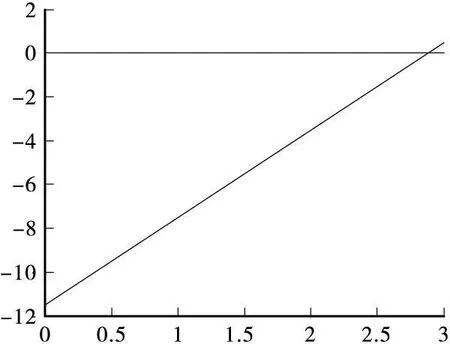
图3 单元①的弯矩图(kN◦m)
f2=BeamElementForces(k2,u2)
f3=BeamElementForces(k3,u3);
f3=f3-[-15;-15;-15;15]
BeamElementShearDiagram(f1,L1)
BeamElementShearDiagram(f2,L2)
BeamElementShearDiagram(f3,L3)
BeamElementMomentDiagram(f1,L1)
BeamElementMomentDiagram(f2,L2)
BeamElementMomentDiagram(f3,L3)
3 结语
本文以平面梁元为例,阐述了基于MATLAB有限元法结构分析。经实践证明,该方法简便、可行、实用。虽然文中以平面梁元为例介绍其应用,但其中的原理和方法可推广到其它单元刚度矩阵,甚至三维空间和非线性刚度矩阵之中,对此,将另文做进一步探讨。
[1]徐荣桥.结构分析的有限元法与MATLAB程序设计[M].北京:人民交通出版社,2006.
[2](德)P.I.Kattan,韩来彬译.MATLAB有限元分析与应用[M].北京:清华大学出版社,2004.
[3](美)Chandrupatla,T,R.,Belegundu,A.D.,曾攀译.工程中的有限元方法(第3版)[M].北京:清华大学出版社,2006.
[4]隋思涟,王 岩.MATLAB语言与工程数据分析[M].北京:清华大学出版社,2009.
[5]包世华.结构力学(第3版,下册)[M].武汉:武汉理工大学出版社,2008.
[6]周水兴,陈山林.MATLAB在有限元刚度矩阵推导中的应用[J].重庆交通学院学报,2007,26(2):29-31.
[7]景振毅,张泽兵,董 霖.MATLAB 7.0实用宝典[M].北京:中国铁道出版社,2009.
[8]丁 星.应用矩阵变换绘制平面刚架内力图和位移图[J].四川建筑科学研究,2010(3).

