边坡排桩支护变形规律探讨

杨 健

(重庆市高新岩土工程勘察设计院,重庆 400042)

0 引言

由于重庆地处丘陵山区,在工程建设的过程中,势必导致大挖大填,形成许多填方边坡,填土粗粒一般为砂岩或泥岩,粒径5～1 000mm,细粒为粉质粘土,土石比一般为6∶4,多为新近无碾压回填,均一性和密实度差,在没有放坡条件下,常采用用衡重式(＜10m)或排桩挡墙。道路工程边坡一般用衡重式挡墙,基坑及无放坡条件的边坡用排桩。排桩一般采用钻孔灌注桩,其抗弯性能差,配筋多,挠度大,因此,必须对桩顶变位进行控制,避免发生塑性挠曲破坏。因此,在完成这类工程后,必须进行监测,并对其变形进行预测,确保变形收敛,并在预测的安全变形之内。本文通过对重庆某边坡支护工程的设计、施工和监测的全过程分析,探讨了桩身为人工填土的排桩的变形规律、变形特点,提出了该类桩变形的预测数学模型和控制方法,并为类似工程积累经验和数据。

1 工程地质概况

人工填土:粉质粘土和块石土组成,粗粒一般为砂岩或泥岩,粒径5～1 000mm,细粒为粉质粘土,土石比一般为6∶4,为新近无碾压回填,支挡处厚度8.0～13.0m。

基岩:为不等厚砂泥岩互层,均为泥质胶结,泥岩为软岩,砂岩为较软岩。

切坡后,在地下车库形成的切坡高度为9.40～12.80m,均为填土边坡,边坡呈L形,总长121 m。

设计中采用参数如表1。

表1 岩土物理力学参数

2 边坡工程支护方案及监测布置

根据该工程现场特点以及甲方要求,即没有放坡距离,要求不能影响其他工地和工序施工,施工期短,经济节省等要求。鉴于此,通过经济和技术对比,最终决定采用钻孔灌注排桩进行支护。桩径φ400 mm和φ500mm,桩间距1m,共120根桩。设计平面布置示意图及排桩设计典型剖面图分见图1、图2。

在最后一根施工完成14 d后,开始边坡开挖,同时对7个监测点进行水平位移监测,为JC 1#～JC 7#,采用视准线法进行观测。

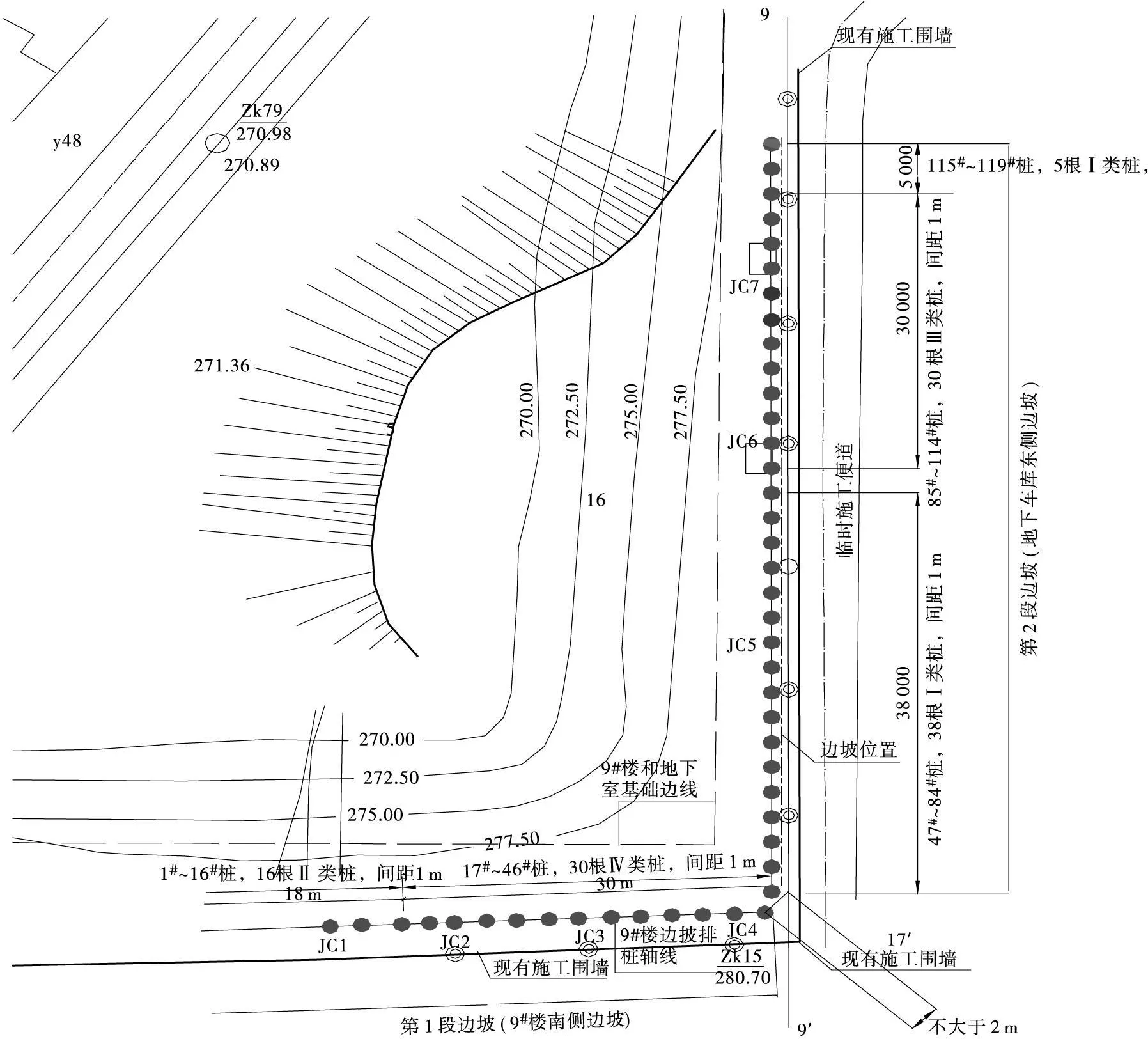
图1 边坡支护工程平面布置图

图2 排桩设计典型剖面图

根据桩的受力特点,采用悬臂梁挠度计算方法对不同的桩分别进行了桩顶变位预测,为监测控制提供依据。这里主要分析JC1#、JC4#、JC5#、JC6#为代表性监测点,悬臂段基本为土层的边坡段。

采用悬臂梁等效计算方法,将其等效为矩形梁后进行挠度计算。

挠度计算公式推导(见图3)如下:

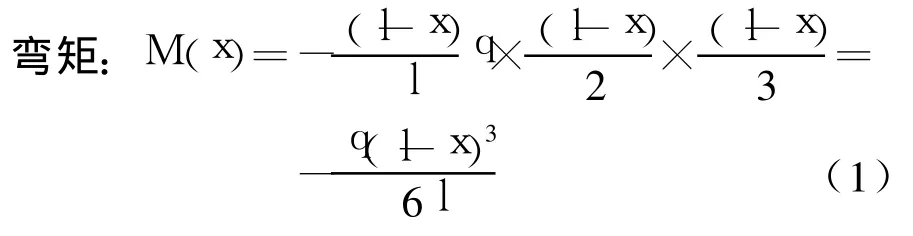
挠曲微分方程为:

将上式连续积分2次,分别得到:

引入边界条件,固定端转角和挠度都等于0,解得:C=0,D=0自由端转角和挠度最大,即:

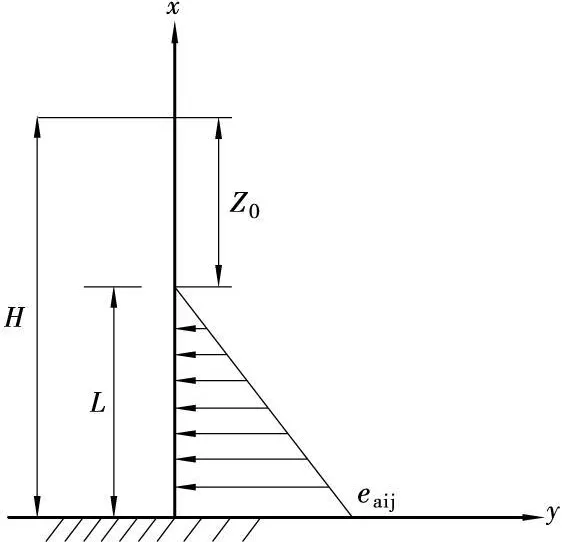
图3 挠度计算公式推导简图

监测代表桩挠度计算成果见表2。

表2 监测代表桩挠度计算成果

3 监测成果及变形规律分析

对7个监测点进行水平位移监测,获得监测数据并作图(见图4)。监测时间从2005—01—11 17:0 0到2005—02—02 09:00,历时22 d。根据对监测曲线的观测分析,可以发现如下规律:

1)各监测点的桩在切坡完成的初期,变形大,桩顶变位快,在后期逐渐趋于平缓,曲线呈收敛趋势,在22 d后变化已经很微小。

2)根据桩径不同、土层厚度不同,桩顶变位的收敛值(变位终值)不同,土层厚度越大,土压力越大,收敛值越大。

3)该收敛曲线特征与指数函数吻合较好,可采用指数函数模拟。

4)监测过程中,桩顶变位具有间歇性。即桩顶达到某一变位值时,会在这一值附近有短暂停滞,然后再继续增长。这一停滞随变形增大而有逐渐延长趋势,直到变形收敛后期,而趋于不明显。

图4 7个监测点的水平位移监测

根据对土体特性分析,该特征主要由土体的蠕变特性引起,当边坡开挖后,桩一侧的抗力失去,在另一侧土体土压力作用下,桩开始发生变形、挠曲,桩顶变位增大;当变位到某一值时,桩后土体会产生较大的裂缝,桩身上部一定范围,桩土分离,土压力不能作用到桩上段,作用点降低,力臂缩短,弯矩减小,变形相对停滞;但由于土体具有不同于混凝土的散体特征,呈明显的蠕变特性,从监测数据看,往往24～72 h后,大部分暂时分离的土体就会蠕动变形而与桩接触,并逐渐将土压力施加到桩上段,作用点上移,当力矩达到一定限值,会再次致桩变形,桩顶变位继续扩大,然后进入下一个循环,如此周而复始,台阶式的桩顶变位跳跃逐渐减小,停滞期逐渐增长,最终趋于平衡而变形终止。显然停滞期的长短与土体的蠕变变形特性直接相关。见图5。

图5 1#监测点跳跃式位移示意图

4 变形收敛曲线函数模拟

4.1 因子分析

影响桩顶变位的因数主要有桩径大小、桩长、混凝土强度、配筋率、土体物理力学强度、土体蠕变性能等。其中排桩的桩径、桩长、混凝土强度、配筋率、土体物理力学强度等,可以用一个指标来综合反映,因为排桩为悬臂桩,可以看作在侧向土压力下的悬臂梁进行挠度计算,即悬臂桩的最大变位或者最终挠度来反映,用λ表示,它显然与桩顶变位的正相关;土体的土体蠕变性能是与时间因素(t)相关的因子,土体蠕变性能好,速度快,则桩顶变位快,显然也是呈正相关,用b表示。

4.2 函数形式选择

通过观测数据的时间变形曲线,该收敛曲线服从形如y=λ×eb◦ta的指数函数。A为不因桩或土体特征变化的常数,通过模拟曲线对比,取a=-0.48,因此公式为y=λ×eb◦t(-0.48)。

4.3 参数确定

将JC1#、JC4#、JC5#、JC6#监测点的数据进行拟合。拟合方法:采用矩阵分析方法,对函数y=λ×eb◦ta解析,以便通过简单的矩阵运算解出需要的常参数λ和b,从而达到拟合目的。解析过程如下:

采用matlab软件编程并进行拟合,得到参数(表3)及模拟曲线。

数据模拟曲线见图6。

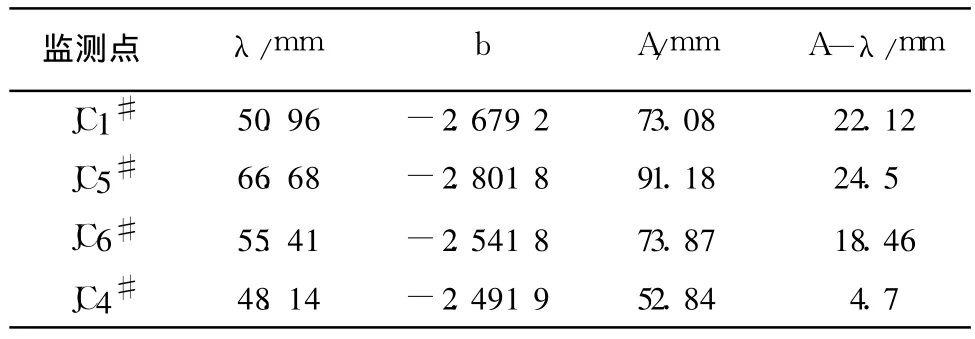
表3 拟合获得参数

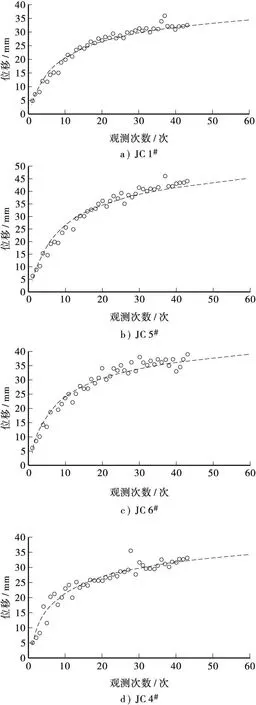
图6 JC 1#、JC 5#、JC 6#、JC 4#监测点拟和曲线

可见通过等效计算挠度值与实际监测位移值差距在4～25 mm,鉴于参数选取和计算方法的限制,挠度估算值往往偏大,可见等效方法计算挠度时略为保守,但可以通过监测过程中的拟合不断修正,位移值差距是允许的,不影响模型建立和预测控制。桩顶变位收敛的预测模型如y=λ×eb◦ta的指数函数。

5 结论

通过排桩支护工程的监测和模型分析,得到以下结论:

1)正常条件下的排桩在变坡开挖,也就是桩开始发生作用后,必然会发生较明显的变位,且变位随时间增大而增大,并逐渐趋于稳定,曲线上表现为收敛,在一个最大的变位幅内,这一变位幅就是桩变形的最大挠度。

2)桩变形并非是沿预测曲线连续不断的变化,而是表现为在每一次急剧变形后,总会有一定的停顿,即“台阶”或“跳跃式”变化,这一停顿是土体通过蠕变进行应力调整的应力调整期,不能在判断上误判为变形开始收敛或有收敛趋势。

3)桩顶变位收敛的预测模型为y=λ×eb◦ta的指数函数,其中影响预测模型函数的因子或参数挠度因子λ和蠕变因子b,都与变位y呈正相关。

[1]郑颖人.岩质建筑边坡岩石压力计算与边坡支护设计[Z].1997.

[2]GB 50330—2002,建筑边坡工程技术规范[S].

[3]JGJ94—94,建筑桩基技术规范[S].