高填方路基过渡段纵向沉降曲线形式探讨
向 烨,周志刚,李炎炎
(1.长沙理工大学,湖南长沙 410004; 2.湖南交通职业技术学院,湖南长沙 410004)
0 引言
公路是国民经济的重要命脉,由于其特有的优越性和灵活性,发挥着其它运输方式所不可替代的作用。截止2009年底,全国公路总里程达386.08万km,比上年末增加13.07万km;其中二级及以上高等级公路里程42.52万km,比上年末增加2.55万km,占公路总里程的11.0%[1]。随着改革开放的持续深入、经济建设的飞速发展以及西部大开发战略的进一步实施,我国高等级公路建设逐渐由东部转向西部,由平原转入山区。在山岭和丘陵等地区的公路建设中,经常会不可避免地碰到高填方路基。
而作为带状三维空间结构物的道路,其走向不仅受宏观规划路线走廊带中主要控制点的制约,而且线路在穿越水网发育地带或丘陵山区时,还受桥涵、高填路基等的影响。这种特殊结构的填土路堤主要分为2类[2],路桥过渡段(桥台与台背一侧填土路堤组成的过渡路段)和填挖过渡段(填土路堤与原山坡体组成的过渡段)。对于前者,由于问题的突出性,很早就有人关注研究,取得一些成果并成功应用于实际工程;但是对于后者,由于相对隐蔽,关于其研究报道主要散见于期刊杂志等。
高填方路基相对一般路基而言:具有填筑高度高、断面面积大、其稳定性需进行专门分析和验算等特点,在公路工程中高路堤一般就是最受重视的分项工程之一。对于高填方路基的填挖过渡路段,其情况更为复杂——地质水文情况差异、路基填高和断面不断变化、大型施工机械不易操作等等,使得高填方路基过渡段的路基沉降问题尤为突出,特别是其不均匀沉降。
然而高填方路基一般要求地基稳定(或者经过相应处理达到工程相关要求),因此其沉降主要为填料自身的压缩沉降和在路面恒载、行车荷载重复作用下的沉降。而车辆经过高填方路基过渡段时由于车辆振动、冲击等动力作用,会进一步加剧其不均匀沉降,不仅加剧路基路面的破坏,还影响行车舒适和安全。
本文结合江西武吉高速公路施工标段相关的工程数据,考虑高填方路基在路面施工完毕,探讨高填方路段过渡段路基纵向沉降曲线形式,为基于车辆动力学考虑车路耦合作用下沉降研究提供分析基础。
1 依托工程概况
大庆至广州国家高速公路是交通部新规划的国家高速路网中的“纵五线”,是纵贯我国东北、华北、华中和华南广大区域的交通运输大动脉。武宁(鄂赣界)至吉安高速公路,是大广线在江西境内的北段,也是江西省“三纵四横”高速公路主骨架的网中“四纵”的一部分。此项目整体式路基横断面宽26.0 m,其组成如下:中央分隔带2.0m+左侧路缘带2×0.75m+超车道2×3.75m+行车道2×3.75 m+硬路肩(含路缘带0.5m)2×3.0 m+土路肩宽2×0.75 m;路基边坡布设如下:路基填高在10m以内边坡坡率均为1∶1.5,其中填土高度8~10 m路段在路基顶面以下2 m处设一宽2 m的平台;填高10~20m时,设两级填方平台,路基顶面以下2 m处设一宽2m的平台,路基顶面以下10m处设一宽1.5m的平台,路基顶面以下0~10m处边坡坡率为1∶1.5;10m以下边坡坡率为1∶1.75;路面结构为4 cm AC—13+6 cm AC—20+8 cm AC—25+8 cm ATB—25+34 cm水泥稳定碎石+20 cm级配碎石。
选取某施工标段的碎石土和红砂岩为研究对象,其压缩试验数据见表1,e—p曲线见图1。

表1 土样压缩试验数据

图1 土样e—p曲线
2 过渡段特征横断面沉降量计算
2.1 土中附加应力和分层总和法
视土基为均匀各向同性半无限弹性体,则竖向集中力Q作用在其表面(见图2),由弹性理论可求得其半无限体内任一点竖向法向应力为[3]:

若在地基表面作用无限分布的线荷载p,则对式(1)中的Q进行积分可求得土体内任一点处的竖向应力[3]:

对于路堤、堤坝等,根据弹性力学的相关知识,均可视为平面应变问题——则对于土体表面作用的均布条形荷载,其分布宽度为b时,对于土体中任一点竖向应力,可将式(2)在荷载宽度b范围内积分,经计算可得:

其中,式(1)~式(3)中各符号含义见图2。
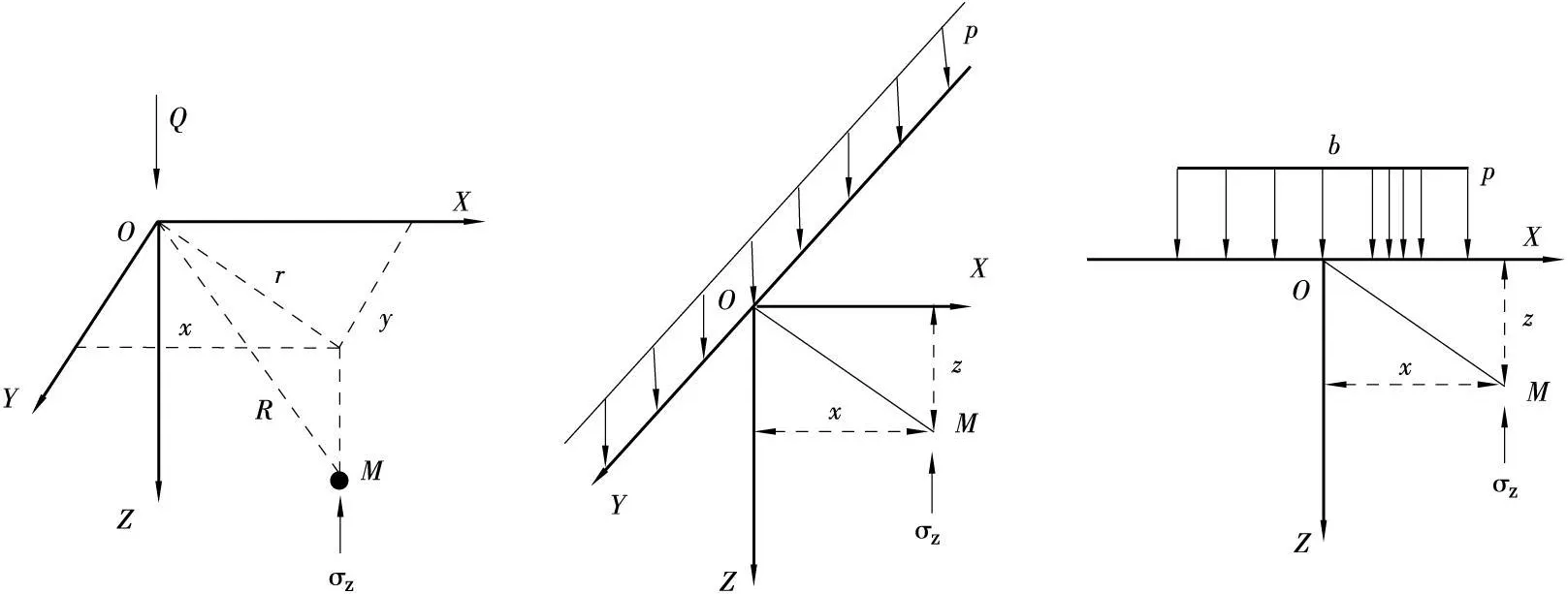
图2 集中力、均布线荷载、均布条形荷载作用下土中应力计算示意图
根据上述土中应力分析基础,针对本文讨论问题的特殊性——重点分析路面施工完毕,路基在路面恒载作用下的沉降变形,采用分层总和法计算路基自身压缩沉降,并作如下假设:
1)填土内部自重应力呈线性增加,按公式a=γh计算,土体中的附加应力符合半无限体上条形荷载作用下的应力分布。
2)随应力水平的逐步变化,填土的孔隙比逐渐减少,压缩模量逐渐提高,其应力应变关系符合e—p曲线或ES—p曲线。采用的分层总和法计算公式如下[3]:

式中:s,Δsi为总沉降量、各分层沉降量,mm;e1i,e2i为对应于第i分层土上下层面自重应力和总应力平均值分别在e-p上对应的孔隙比;hi为第i层土层厚度,mm。
2.2 横断面沉降计算点位选择
对于路基沉降值计算,特别是在路基设计与施工过程中的观测控制等,大多数优先选取道路中心线为计算或者观测点位,但对于本论文探讨的问题,显然不合适。为了与车辆动力学分析提供更贴近实际的分析基础,本文根据行车道宽度和车型宽度选择横断面上的计算点位,即式(3)中x的取值。
本文综合考虑,取行车道的行车位置为计算点位,计算公式如下:令路基中心线为原点,则x=1/2中分带宽+左侧路缘带宽+超车道宽度+1/2行车道宽-1/2设计车辆宽(假设车辆中心线与行车道中心线重合)。根据规范[4]提供的设计车辆(载重汽车和鞍式列车)的总宽度为2.5 m,则根据横断面布设,取x=6.125m。
2.3 过渡段特征横断面沉降值计算
路基横断面宽26m,路面结构厚度为0.8m,边坡坡率为1∶1.5,则路基顶面宽度b=28.4m,路面恒载产生的均布压力p=20 kPa(其路面材料重度取均值25 kN/m3),碎石土自重γ1=20.28 kN/m3,红砂岩自重γ2=21.33 kN/m3,则根据式(3)计算路面恒载在路基中产生的附加应力,由e—p压缩曲线计算不同各个分层所对应的孔隙比,采用式(4)计算各层沉降压缩量,并求和,计算结果见2表。

表2 典型断面的路基压缩沉降量
3 过渡段纵向沉降曲线拟合
3.1 过渡段纵向沉降曲线形式分析
由于过渡段衔接一般路段和高填方路段,理想情况下,正常路段和高填方路段的沉降趋于一恒定值,而过渡段的沉降值则按照一定的规律变化。文献[5]从行车舒适性角度出发,采用抛物线形式,模拟路基路面纵向沉降曲线确定路基沉降标准;文献[6]通过对路桥过渡段路面的差异沉降特性进行分析,采用指数形式模拟路桥过渡段纵断面方向的路面沉降;文献[7]假设填挖交界处到正常路堤的路表沉降曲线为三次多项式u(x)=u0(x/L)2(-2x/L+3),然后分析对路面结构的影响,式中u(x)为路基顶面某点的沉降量,u0为路堤顶面最大沉降量,L为特征长度,即路堤最大沉降点与填挖交界点之间的距离。
考虑本文所讨论的问题,所采取的纵向沉降曲线y=f(x),需满足以下条件:
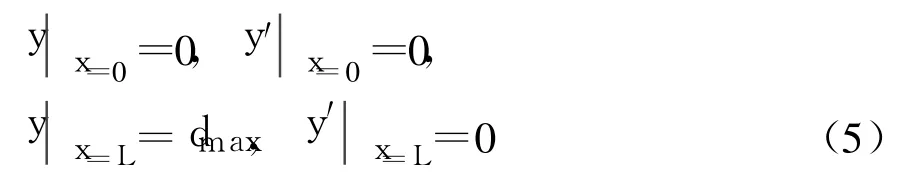
式中:y为路面的沉降值,mm;x为路面沉降计算点到过渡段起点距离,m;L为过渡段长度,m;dmax为高填方路段恒定沉降值,mm,等于过渡段结束时的最大沉降值。
分析各种曲线形式,结合自身工程实践与相关经验,采用曲线组合形式,即幂函数和抛物线的组合形式:

a、b、c为拟合参数。此形式以满足式(5)中的大部分条件,其中的的条件引申出来系数关系不会严格满足,不过经过数学相关拟合等处理,可以满足计算精度要求。
为了体现不同沉降量的影响,对式(6)进行如下调整:
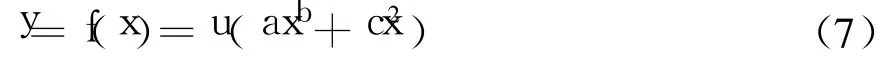
式中u为高填方路段恒定沉降值,mm,等于过渡段结束时的最大沉降值,其余符号意义同前。
3.2 不同坡度的沉降曲线拟合
考虑低山丘岭地区地形的地面自然坡度,一般在10°~30°之间,本次计算坡度依次取10°、15°、20°、25°、30°和35°这6个数值,根据上述确定的典型断面,则不同坡度不同路基填高对应的过渡段纵向水平长度计算见表3。

表3 不同地面坡度不同填高横断面所对应的纵向水平长度
根据计算的典型横断面沉降值和不同地面坡度对应的水平距离,用数值计算分析软件拟合式(7),并求解相关参数。1stOpt是七维高科有限公司(7D-Soft High Technology Inc.)独立开发,拥有完全自主知识产权的数学优化分析综合工具软件包。在非线性回归,曲线拟合,非线性复杂模型参数估算求解,线性/非线性规划等领域居世界领先地位[8]。本次拟合即采用1stOpt1.5专业版,计算结果见表4。
由表4计算值易知,式(7)中的参数值随坡度的不同而变化,但对于同一种土类来讲,参数b的数值基本稳定在某数值附近——碎石土,b大致为1.05;红砂岩,b大致为1.04。这说明所选拟合公式是正确的,反映了路基纵向沉降的基本规律;同时残差均方差、相关系数、决定系数、卡方系数、F统计等数学计算值和假设检验等,也从另一方面验证了拟合公式的合理性和正确性。
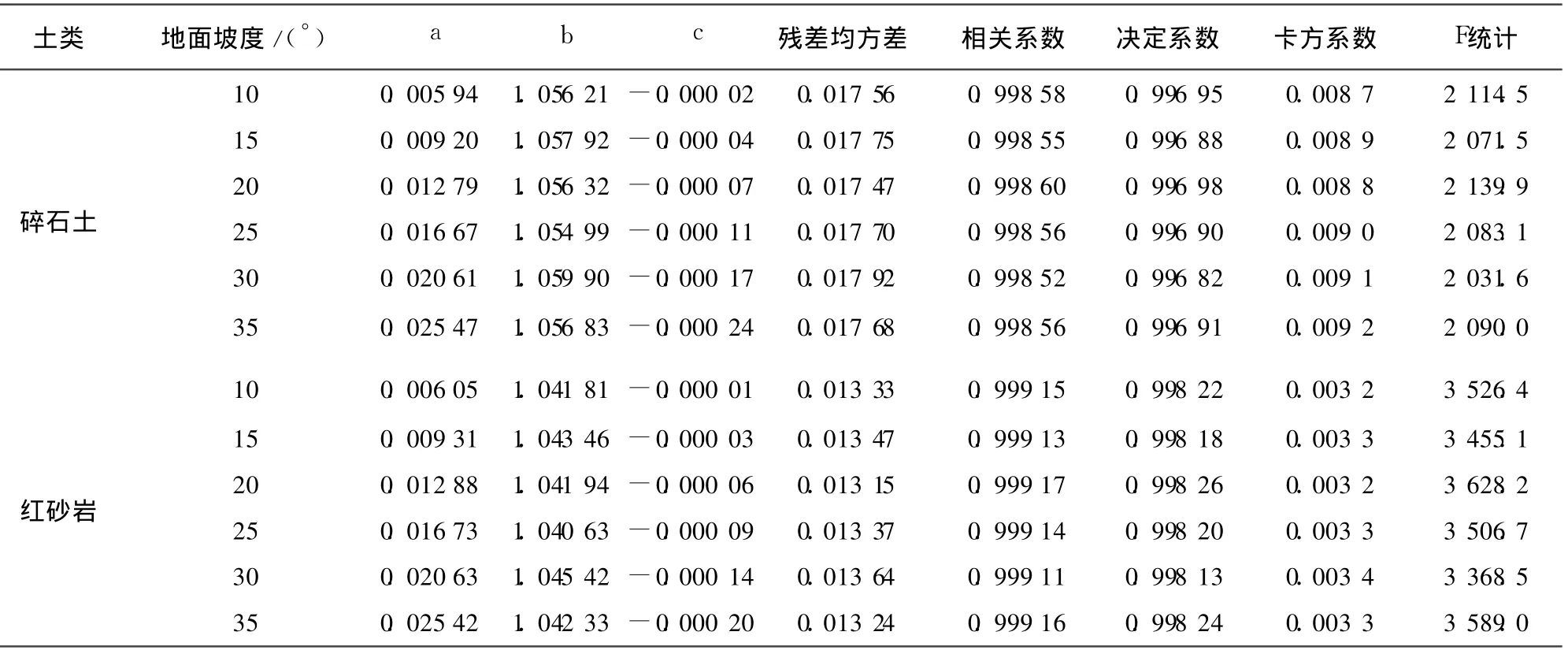
表4 纵向沉降曲线参数拟合值
4 结论与建议
本文结合工程实例确定高填方路基过渡段的特征横断面的路基填高,并分析合理的沉降计算点位,采用分层总和法计算路基压缩沉降值;根据实际情况分析过渡段路基纵向沉降曲线的合理形式,采用1stOpt分析软件拟合沉降曲线的参数,验证了所选沉降曲线形式的合理性,为基于车辆动力学考虑车路耦合作用下沉降研究提供分析基础。
不过,鉴于工程实际和笔者自身水平,以下问题有待进一步考虑:
1)本文仅考虑路基自身的沉降量,应该把地基的沉降值一起考虑进来,不过问题将变得复杂;
2)高填方路基过渡段纵向沉降曲线的形式应进一步优化,最好结合工程观测实际,进行数值拟合;
3)本文仅列出2类土的计算结果,应扩大填料的种类,以进一步验证优化沉降曲线,并为类似工程提供参考。
[1]中华人民共和国交通运输部.2009年公路水路交通运输行业发展统计公报[R].2010.
[2]丁 浩.高速公路特殊结构的填土路堤变形特性及相关公路病害研究[D].北京:中国地质大学,2002.
[3]高大钊,袁聚云.土质学与土力学[M].北京:人民交通教育出版社,2001.
[4]JTGB01-2003,公路工程技术标准[S].
[5]唐 娴.路基沉降机理与超限沉降标准的研究[D].西安:长安大学,2003.
[6]陶向华.路桥过渡段差异沉降控制标准与人车路相互作用[D].东南大学,2006.
[7]李 强,周志刚,郑健龙.填挖交界处路基不均匀沉降对路面结构的影响[Z].第四届国际道路和机场路面技术大会,2002.
[8]七维高科.1stOpt使用手册[Z].2009.

