基于损伤理论对岩土边坡的流固耦合分析
张必双
(湖南省怀化路桥建设总公司,湖南怀化 419502)
在渗流场及应力场的相互耦合作用下,岩土体的破坏过程是与其内部微裂缝的萌生、演化与发展密切相关的。即在渗流场和应力场的作用下,岩土材料本身的材料特性会逐步降低,而不是一成不变的。目前国内外引入损伤理论对岩土体进行流固耦合分析的研究开展很少。因此,在前人的研究基础上,本文意图在流固耦合分析时,引入损伤理论对岩土体的变形破坏过程进行数值模拟分析,这将对岩土体滑坡的预报与治理都有巨大的理论指导意义[1,2]。
1 损伤原理
采用损伤力学研究岩土体结构破损的优势在于可用损伤来描述土体微观结构的破损过程,找到损伤的演化规律,建立起基于损伤变量的本构模型,从而更加切合实际地描述岩土体受力后到破损的过程。然而损伤理论最初由金属材料发展而来,由于岩土材料的不规则性,如何定义损伤变量成为将损伤理论应用于岩土工程的难点[3,4]。沈珠江[5]在20世纪80年代,最早提出了土体损伤理论。沈珠江建议的损伤比ω=1-e-(αεv+εs)(其中:εv=ε1+ε2+考虑因素虽较全面,但在实际应用时参数确定假设条件较多,试验方法也较繁琐,不易于应用。
根据沈珠江(1993)提出的土体损伤理论[6-8],天然土体可看作由理想的原状土和完全损伤土(重塑土)组合而成。土体在受荷作用之下的变形过程可看作是由原状土向损伤土的演变过程,其力学特性是变形过程中2种土特性的综合反映,因此其力学参数可由下式表示:

式中,S为天然土体的力学参数;Si为原状土的力学参数;Sd为损伤土的相应力学参数;ω为损伤比,即损伤部分在整个土体中所占的比重。
2 工程概况
选取某高速公路边坡为依托工程进行模拟,其边坡土层分为上下两层,上层系以第四系松散堆积物(Qdl+el)为主体的坡体,厚12~16m,下层基岩系以中风化泥质粉砂岩为主体的上二迭系龙潭组(P2l)煤系地层。在室内外试验及现场勘察资料的基础上,选取边坡岩土力学参数如表1所示。
FLAC3D可以模拟多孔介质中的流体流动,比如地下水在土体中的渗流问题。FLAC3D既可以单独进行流体计算,只考虑渗流的作用,也可以将流体计算与力学计算进行耦合,具有强大的渗流计算功能,因此本文选用FLAC3D作为模拟工具。
位移边界条件:固定模型左右边界x方向的位移,固定底面基岩x、y、z方向的位移,固定模型y方向的位移。

表1 岩土力学参数
渗流边界条件:模型左右两侧均为不透水边界,顶部坡面为自由透水面。
初始应力场:采用FLAC3D中的弹性求解法生成初始应力场。
3 模拟结果
图1、图2为岩土体边坡在考虑流固耦合的水平X方向及竖直Z方向位移云图,通过对比不同损伤比情况下的云图,可以得到以下结果:
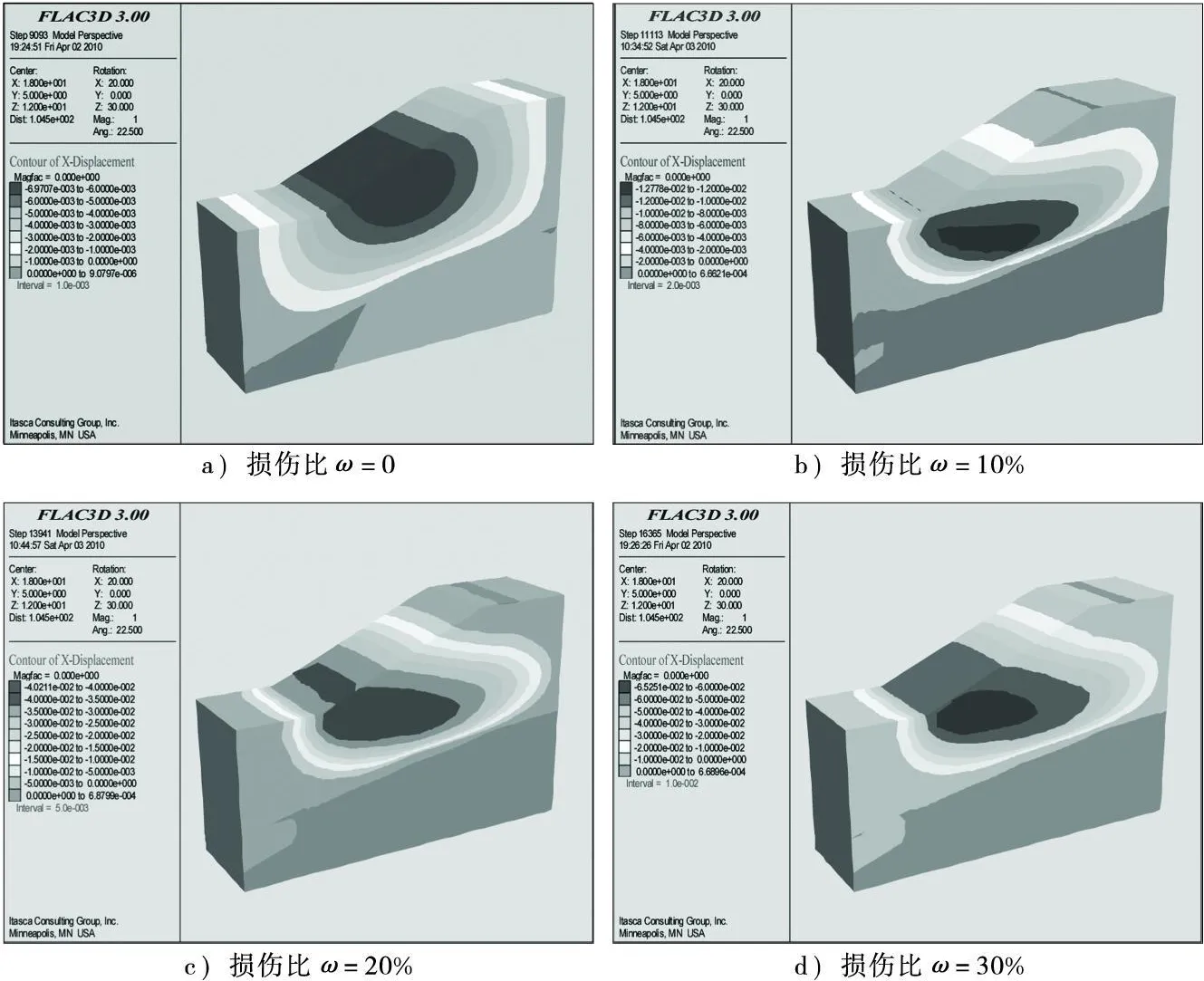
图1 水平X方向位移云图(单位:m)
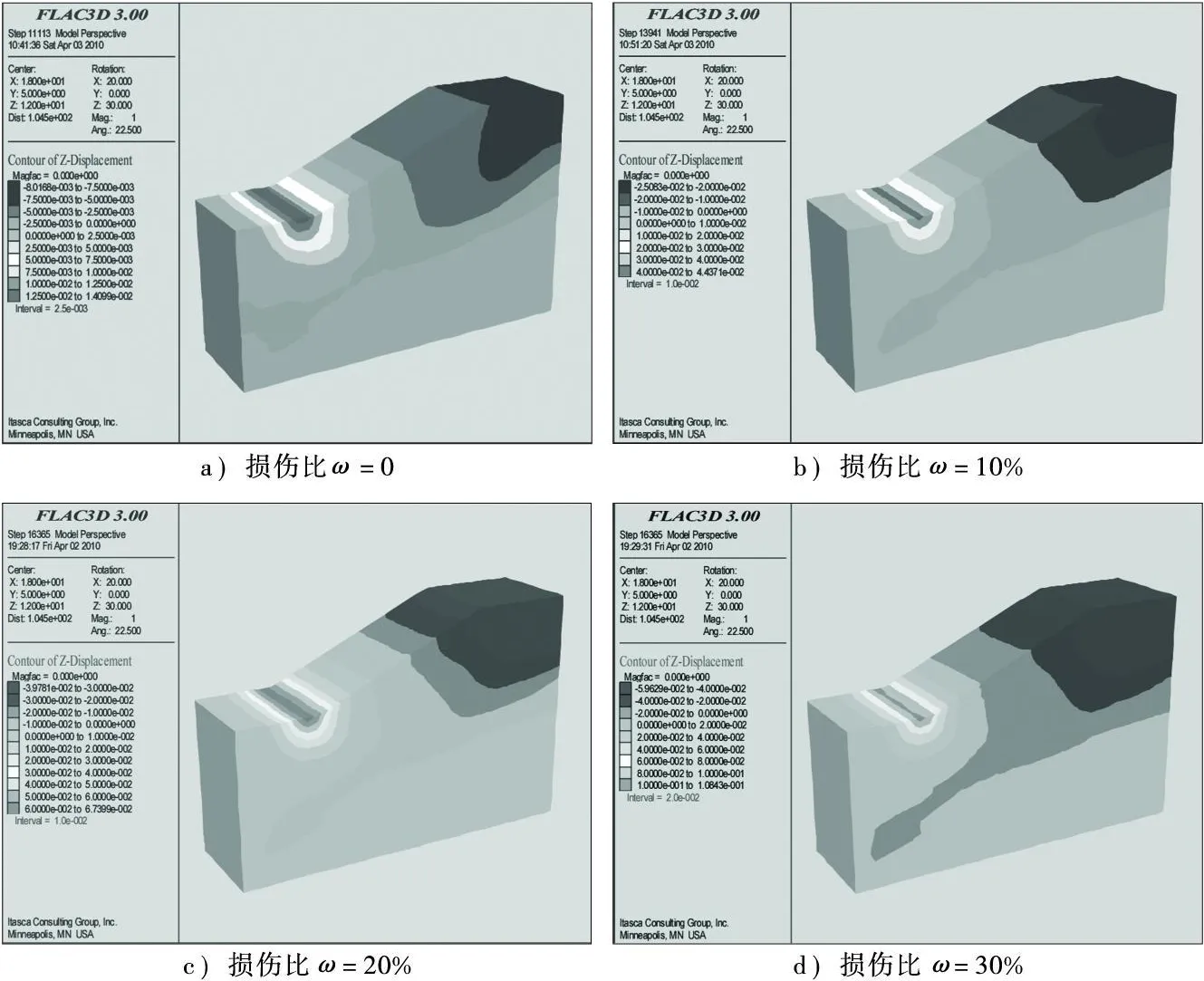
图2 竖直Z方向位移云图(单位:m)
1)水平X方向的最大位移出现在坡面的下半部分,即坡脚处并有向内部延伸趋势。其最大值在未考虑损伤的情况下为7.0mm;损伤比为10%时为12.8mm;损伤比为20%时为40.0mm;损伤比为30%时为65.3mm。在工况2情况下,其最大值在未考虑损伤的情况下为735.2mm;损伤比为10%时为817.7mm;损伤比为20%时为919.2 mm;损伤比为30%时为1 026.6mm。为了更直观的表明其X向位移与损伤的关系,见图3。
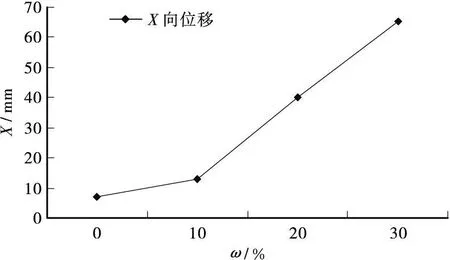
图3 X向最大位移
2)竖直方向在坡顶处出现了较大的下沉位移,并且随着损伤比的增大,其下沉值也越大。其最大值在未考虑损伤时为8.0mm;损伤比为10%时为25.1mm;损伤比为20%时为39.8mm;损伤比为30%时为59.6 mm。
在坡脚处则出现了上升位移,即坡脚出现了隆起。这是因为在坡顶土下沉的影响下,坡脚处土体收到内部土体的推力,因此出现了向上的隆起,如果位移过大的则会出现坡体失稳或滑坡。上升位移集中分布在坡脚处,分布范围不是很大。其最大值在未考虑损伤时为12.5mm;在损伤比为10%时为44.4mm;损伤比为20%时为67.4mm;损伤比为30%时为108.4 mm。见图4。
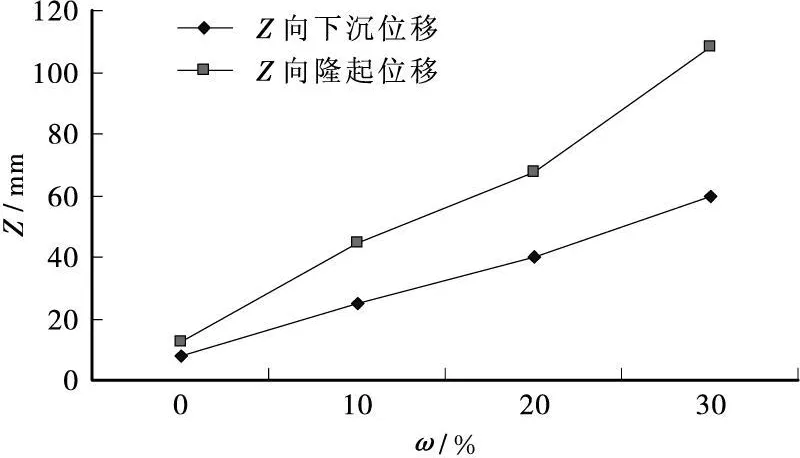
图4 Z向最大位移
可以看出,随着损伤比的增大,坡体的水平和竖向位移也随之增大,并且在损伤比达到20%时,水平位移的最大值出现了较大幅度的增大;竖向位移在损伤比达到30%时,其坡脚处的位移增大明显,并且在岩层分界面处也出现了较大位移。
4 结论
基于不同的损伤比应用FLAC3D对土石混合体边坡进行流固耦合分析,结果表明:损伤比对位移场影响比较明显,随着损伤比的增大,坡体的水平位移和竖向位移也随之增大,并且在损伤比达到20%~30%时,位移的最大值出现了较大幅度的增大。从模拟结果来看损伤发展对坡体结构性起到了弱化的作用,因此,在边坡稳定性分析中应给予重视。
[1]吴小策.降雨入渗对土石混合体边坡稳定性影响机理研究[D].长沙:中南大学,2010.
[2]周 中.土石混合体滑坡的流-固耦合特性及其预测预报研究[D].长沙:中南大学,2006.
[3]蒋仓兰,等.损伤理论在岩土工程中的应用[J].华北水利水电学院学报,2007(4):81-84.
[4]赵锡宏.损伤土力学[M].上海:同济大学出版社,2002.
[5]沈珠江,张为民.损伤力学在土力学中的应用[A].第三届全国岩土力学数值分析与解析方法讨论会[Z],1988.
[6]沈珠江.结构性粘土的堆砌体模型[J].岩土力学,2000,21(1):1-4.
[7]沈珠江.结构性粘土的弹塑性损伤模型[J].岩土工程学报,1993,15(3):1-6.
[8]沈珠江.结构性粘土的非线性损伤力学模型[J].水利水运科学研究,1993(3):247-255.
[9]李建红,沈珠江.结构性土的微观破损机理研究[J].岩土力学,2007(8).
[10]熊玉春,房营光.饱和软粘土地基的损伤模型与震陷计算[J].振动工程学报,2006(3).
[11]李杭州,廖红建,盛 谦.基于统一强度理论的软岩损伤统计本构模型研究[J].岩石力学与工程学报,2006(7).
[12]熊传祥,龚晓南.一种改进的软土结构性弹塑性损伤模型[J].岩土力学,2006(3).
[13]吕海波,赵艳林,孔令伟,等.利用压汞试验确定软土结构性损伤模型参数[J].岩石力学与工程学报,2005(5).
[14]陈铁林,周 成,沈珠江.粘土变形特性分析[J].岩土力学,2004(4).
[15]何开胜,沈珠江.结构性粘土的弹粘塑损伤模型[J].水利水运工程学报,2002(4).

