Banach空间中Xd-Bessel列的广义扰动

刘 楠, 刘 琴, 曹怀信

(1.陕西师范大学数学与信息科学学院, 陕西 西安 710062;2.陕西工业职业技术学院基础部, 陕西 咸阳 712000)

0 引言

从上个世纪90年代开始，Grochenig[1]， Aldroubi， Sung和Tang[2]先后在Banach空间中引入了两种不同的框架概念: Banach框架和p-框架．我们知道Hilbert空间H中一定存在框架(例如正规正交基)，并且Hilbert空间中的框架一定具有对偶框架，参见文[3, 4]．但是，在Banach空间中上述结论不再成立．为了讨论Banach空间中Banach框架的存在性问题和元素的重构问题，Casazza在文[5]中将文献中的p-框架概念进行了推广，引入了Xd-框架的概念，并且给出了Banach空间中Banach框架存在的充要条件，以及Xd-框架具有重构性的若干充要条件．张建中和吕桂莉在文献[6]中讨论了Banach空间中的Xd-框架及其稳定性. Stoeva在文[7]中探讨了有关Xd-框架、Xd-框架的对偶及Xd-框架的扰动性的一些结论．本文主要根据文[8]的一些结论，利用算子论的方法，结合代数的思想，讨论了Bananch空间中Xd-Bessel列的广义扰动．

1 预备知识

本文用N表示非零自然数集，F表示复数集或者实数集，X表示数域F上的可分Banach空间.

设Xd为数域F中以N为指标集的序列组成的赋范线性空间．∀i∈N，定义泛函Pi∶Xd→F为

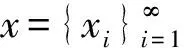
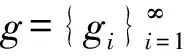
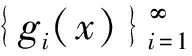
(2) 存在常数B>0，使得:

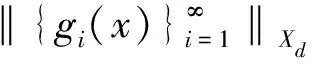
则称g为X的Xd-Bessel列．记

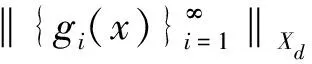
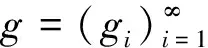
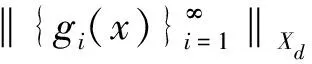
设X是Banach空间，Xd为BK-空间．记

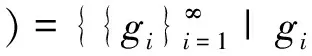
则BXd(X)⊂S(X*)．

定义1.2 设Xd是一个包含所有典范向量ei(i∈N)的BK-空间，定义:

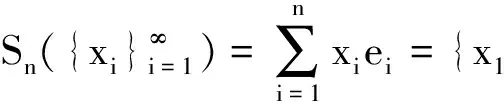
若存在λ≥1,使得

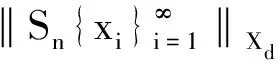
即

‖Snx‖Xd≤λ‖x‖Xd,∀n∈N,∀x∈Xd

即

‖Sn‖≤λ，∀n∈N

则称Xd为一个λ-BK-空间．

∀f,g∈BXd(X)，∀λ，μ∈F,定义

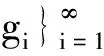
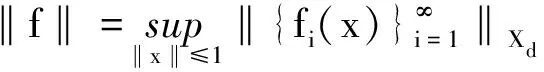
定理1.1[8](1)若Xd为BK-空间，则(BXd(X),‖·‖)是数域F上的赋范线性空间；(2)若Xd为CB-空间，则(BXd(X),‖·‖)是数域F上的Banach空间．

2 Xd-Bessel列的广义扰动

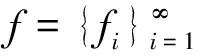
证明若f∈BXd(X)，上界为Bf, 则由定义1.2知，∀n∈N,∀x∈X,

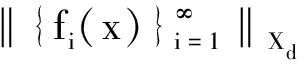
故g∈BXd(X)，且Bg≤λBf. 证毕.

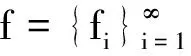
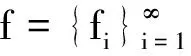
‖g(x)‖Xd=‖(h-k)(x)‖Xd≤‖h(x)‖Xd+‖k(x)‖Xd≤(Bh+Bk)‖x‖≤2λBf‖x‖

故g∈BXd(X)，且Bg≤2λBf. 证毕.

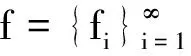
证明若f∈BXd(X), 上界为Bf,令h={f1,…,fn,0,…}，则由定理2.1知，h∈BXd(X)，且Bh≤λBf，再由定理1.1结论(1)知，g=f-h∈BXd(X)，且

‖g(x)‖Xd=‖(f-h)(x)‖Xd≤‖f(x)‖Xd+‖h(x)‖Xd≤(Bf+Bh)‖x‖≤(1+λ)Bf‖x‖

故g∈BXd(X)，且Bg≤(1+λ)Bf. 证毕.

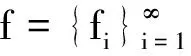
证明若f∈BXd(X)，上界为Bf, 则∀x∈X，结合推论2.1有

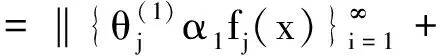
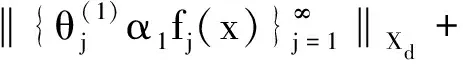
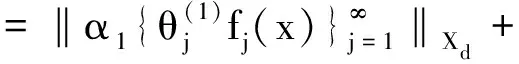
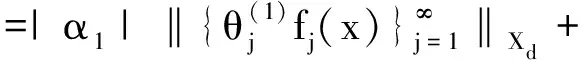
≤|α1|2λBf‖x‖+…+|αi|2λBf‖x‖+…

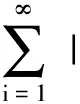
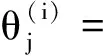
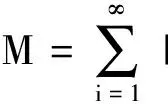
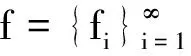
证明由f∈BXd(X)，上界为Bf,有

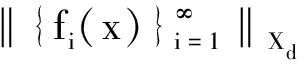
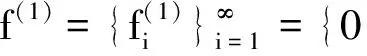
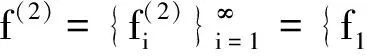
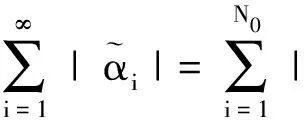
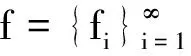
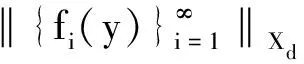
且

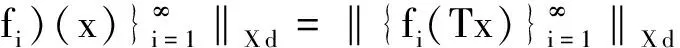
故g∈BXd(X). 证毕.

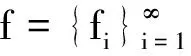
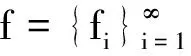
证明设f∈BXd(Y),上界为Bf,有

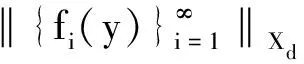
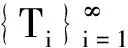
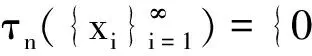
从而

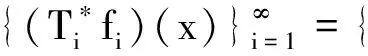
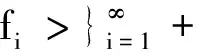
结合推论2.1有

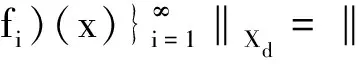
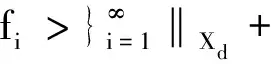
≤2λBf‖T1x‖+…+2λBf‖Tjx‖+…

≤2λBf‖T1‖·‖x‖+…+2λBf‖Ti‖·‖x‖+…

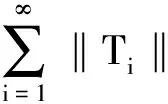
故g∈BXd(X). 证毕.

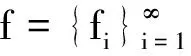
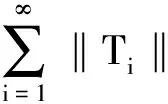
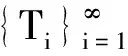
证明由f∈BXd(Y)，上界为Bf,有

[1]Grochenig K. Describing functions: atomic decompositions versus frames[J]. Monat- shefte Mathematik, 1991, 112: 1-41.

[2] Aldroubi A. Sung Q and Tang W,p-frames and shift invariant subpaces ofLp[J].Journal of Fourier Analysis and Applications,2001, 7: 1-22.

[3] Favier J S and Zalik R A. On stability of frames and Riesz bases[J]. Applied and Computational Harmonic Analysis,1995, 2: 160-173.

[4] Christensen O. A Introduction to Frames and Riesz Bases[M]. Boston: Birkhauser, 2003.

[5] Casazza P, Christebsen O. and Stoevs D. Frame expansions in separable Banach spaces[J]. Journal of Mathematical Analysis and Applications, 2005, 1:1-14.

[6] 张建中,吕桂莉. Banach空间中的Xd-框架及其稳定性[J]. 山东科技大学学报(自然科学版), 2008, 27(1): 91-93.

[7] Diana T. Stoeva, Perturbation of frames in Banach spaces[EB/OL]. Available online at ArXiv, 2009.

[8] 刘 楠, 曹怀信.Banach空间中的Xd-Bessel列的性质[J].陕西师范大学学报,2010(待发).