箱梁截面尺寸对横向温度应力影响的分析

李建国,季日臣

(兰州交通大学土木工程学院,甘肃兰州730070)

0 引言

混凝土结构置于自然环境中,长期受到自然界气温的变化和日照辐射等作用。由于混凝土的热传导性能相对较差,在周围环境温度和日照辐射等作用下,使得其表面温度迅速变化,而其内部保持原来的状态,从而产生较大的温度变形,当这些变形受到约束后就产生了温度应力。有时温度产生的应力比荷载产生的应力还大,很多混凝土桥梁因此产生了严重的裂缝。因此,温度应力问题成为了混凝土桥梁设计和施工的一个重要课题。

随着桥梁结构向大跨、薄壁、轻型和整体性的方向发展,预应力混凝土箱形梁的应用日益广泛[1]。现代桥梁设计中对于桥梁的温度效应有所考虑,但在近年的大跨度预应力混凝土箱梁的施工过程或运营过程中均出现了不同程度的纵向裂缝。经分析,这些裂缝是由横向温度应力产生的。因此,在设计和施工中加强对横向温度应力的控制是非常重要的。

1 横向温度应力计算理论

大量资料表明,在桥长方向的温度分布一般是很接近的,从工程实用的角度考虑,略去桥长方向温差的影响是允许的。在箱梁截面上,由于其水平方向热传导远小于垂直方向的热传导,在工程计算中可忽略其水平方向的热传导。因此本文采取一维的竖向温度分布曲线对箱梁进行横向温度应力分析,即现行铁路规范《铁路桥涵钢筋混凝土和预应力混凝土结构规范》(TB10002.3-2005)温度分布曲线,其分布形式见图1。

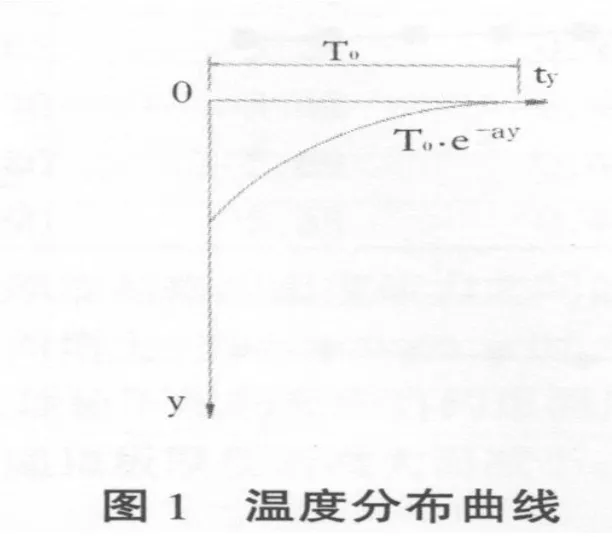
现行铁路规范温度分布曲线的函数形式如下：

式中：T0为顶、底板的温差,本文取T0=20℃;a为温度分布曲线指数,该值随结构形式、部位方向、计算时刻等因素影响,本文取a=5。

横向温度应力由横向局部温度自约束应力和横向框架约束温度应力两部分组成。横向温度自约束应力可按非线性温度分布下的矩形板条自约束应力计算;横向框架温度约束应力可按横向框架计算,先求出线性温度分布下的横向约束温度应力,然后再乘以非线性温度分布的修正系数k[3]。横向局部温度自约束应力计算采用规范中的公式,其形式如下：

式中：δ为板厚(m);α为线膨胀系数,本文取α=0.000 01为板厚范围内的温度,=T0(1-e-aδ);y为计算点至外表面距离(m);a′为沿板厚温度曲线指数(m-1),本文取a′=10;k1、k2为计算系数(查沿板厚日照温差应力计算系数表)。

横向框架约束温度应力的计算公式采用规范中的公式,其形式如下：

式中：γ=b/h(b为梁底宽,h为梁高);yi为板内计算点至外表面的距离(m);k为沿板厚温度分布的非线性系数(查沿板厚日照温差应力计算系数表)。

2 算例分析

2.1 工程概况

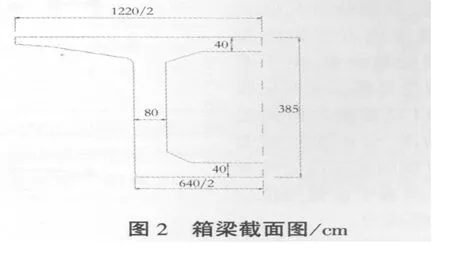
以京石客用专线跨石铜公路(52+88+88+52)m预应力混凝土连续梁桥为例,该桥采用挂篮悬臂对称施工,边支座中心线至梁端0.75 m,桥梁全长281.5 m,现浇箱梁为单箱单室,变高度、变截面结构,梁高沿纵向按二次抛物线变化,抛物线方程为y=-0.001 94x2,中支点梁高6.65 m,边支点及跨中梁高3.85 m,墩顶直线段长9 m,边跨直线段长13.25 m。

截面采用单箱单室直腹板形式,顶板厚度为40～100 cm,局部加宽为130 cm,腹板厚50～90 cm,底板厚度为40～100 cm。顶板宽12.2 m,底板宽度6.4 m。箱梁两侧腹板与顶底板相交处均采用圆弧倒角过渡。支座处共设置5个横隔板,横隔板厚度：边支座处1.25 m,中支座处2.4 m。横隔板设有孔洞,供检查人员通过。梁体采用C50混凝土。

2.2 计算结果分析

从箱梁截面尺寸方面分析横向温度应力,以箱梁某些尺寸的变化分析横向温度应力的变化特点。因为箱梁的顶板宽度和底板宽度不变,所以这两项尺寸不能作为变量来分析横向温度应力。以梁高、顶板厚度、底板厚度、腹板厚度项为变量,分别分析其变化与横向温度应力变化的关系。在箱梁截面中,由于箱梁的顶板受日照温度变化最显著,所以以顶板的横向温度应力为准,分析箱梁截面的尺寸对横向温度应力的影响。本文图表中正值为拉应力,负值为压应力。

⑴横向温度应力随梁高的变化关系见图3和表1。

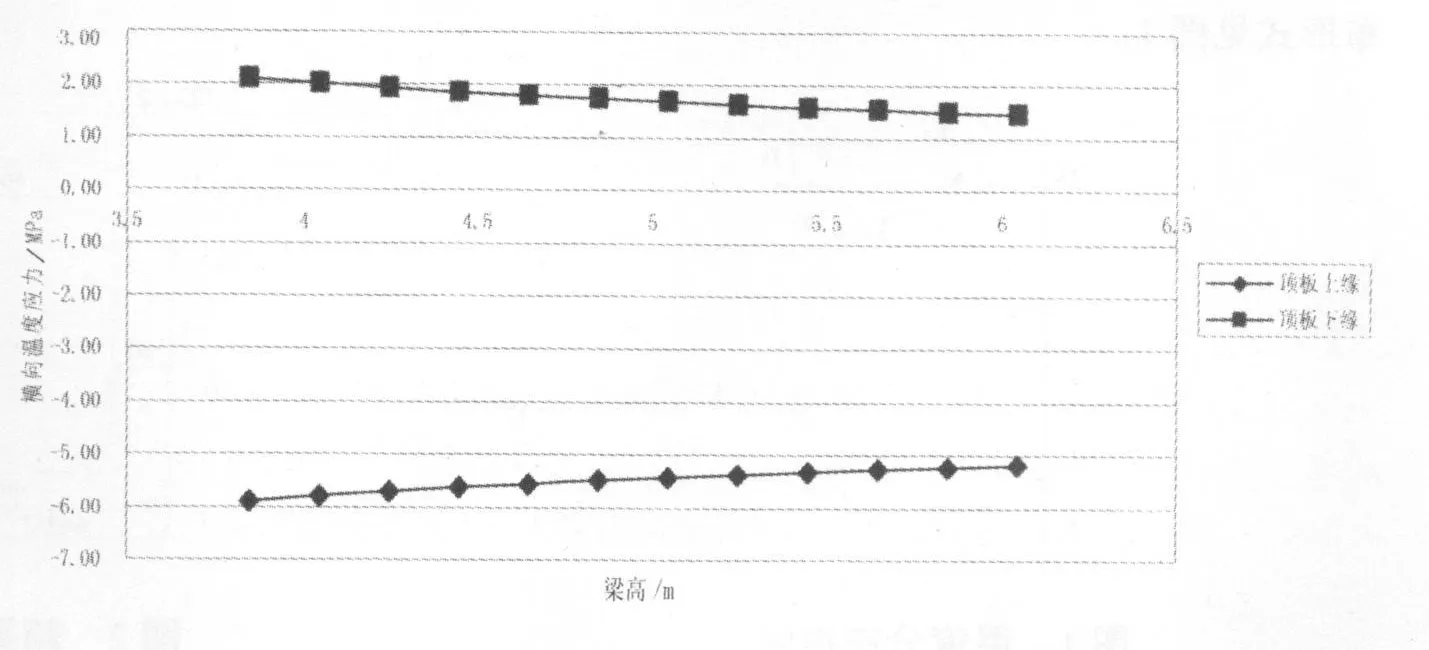
图3 横向温度应力随梁高的变化曲线图

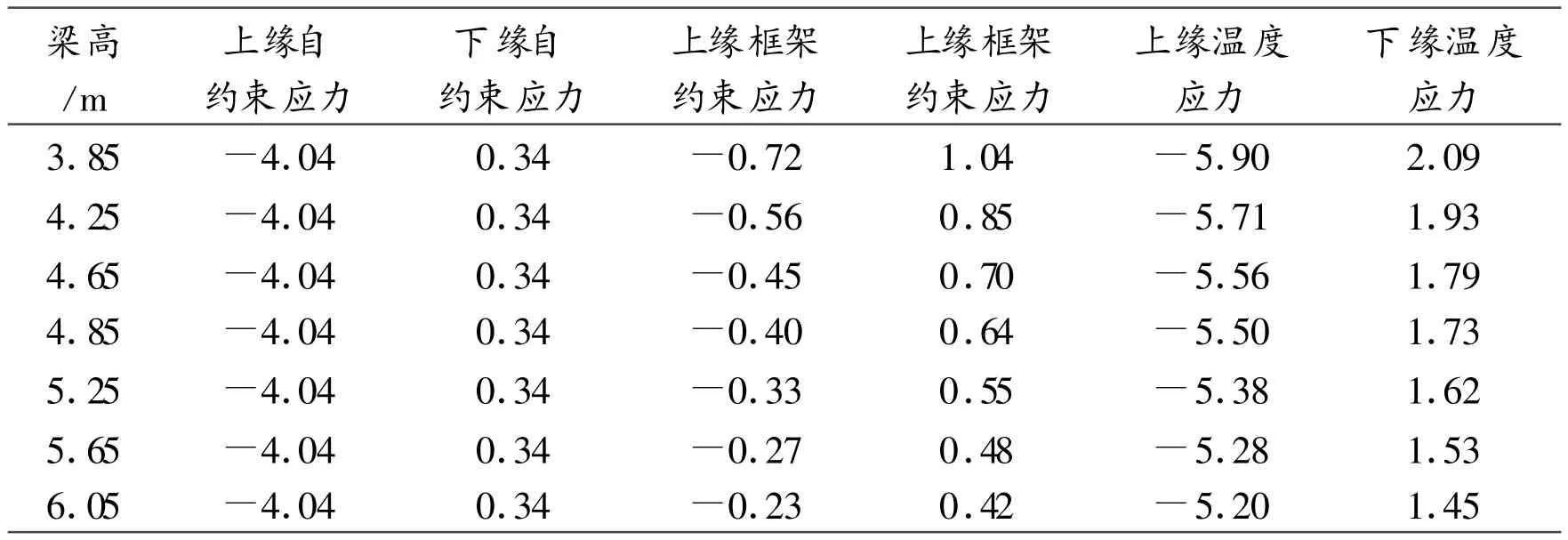
表1 横向温度应力随梁高的变化表/MPa

梁高与横向温度应力之间的变化关系有如下特点：梁高对顶板上、下缘的横向温度自约束应力的影响很小;梁高对顶板上、下缘的横向框架温度约束应力的影响比较明显,且顶板上、下缘的横向框架温度约束应力随梁高的增大而减小。

⑵横向温度应力随顶板厚度的变化关系见图4和表2。

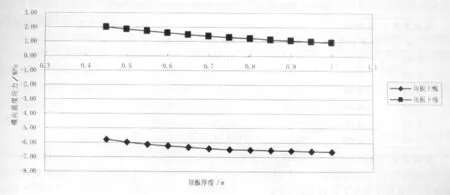
图4 横向温度应力随顶板厚度的变化曲线图

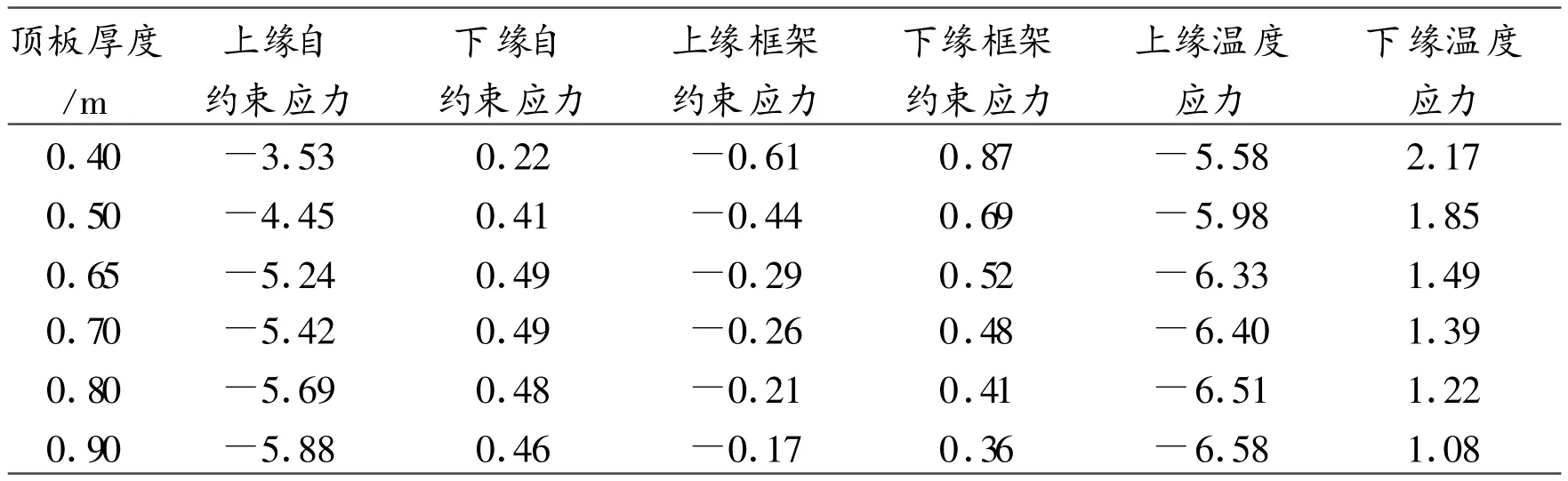
表2 横向温度应力随顶板厚度的变化表/MPa

顶板厚度与横向温度应力之间的变化关系有如下特点：顶板上缘的横向自约束温度应力随顶板厚度的增大而增大;当小于0.65 m时,顶板下缘的横向自约束温度应力随顶板厚度的增大而增大;当大于0.7 m时,顶板下缘的横向自约束温度应力随顶板厚度的增大而减小;顶板上、下缘的横向框架约束温度应力均随顶板厚度的增大而减小。

⑶横向温度应力随底板厚度的变化关系见图5和表3。

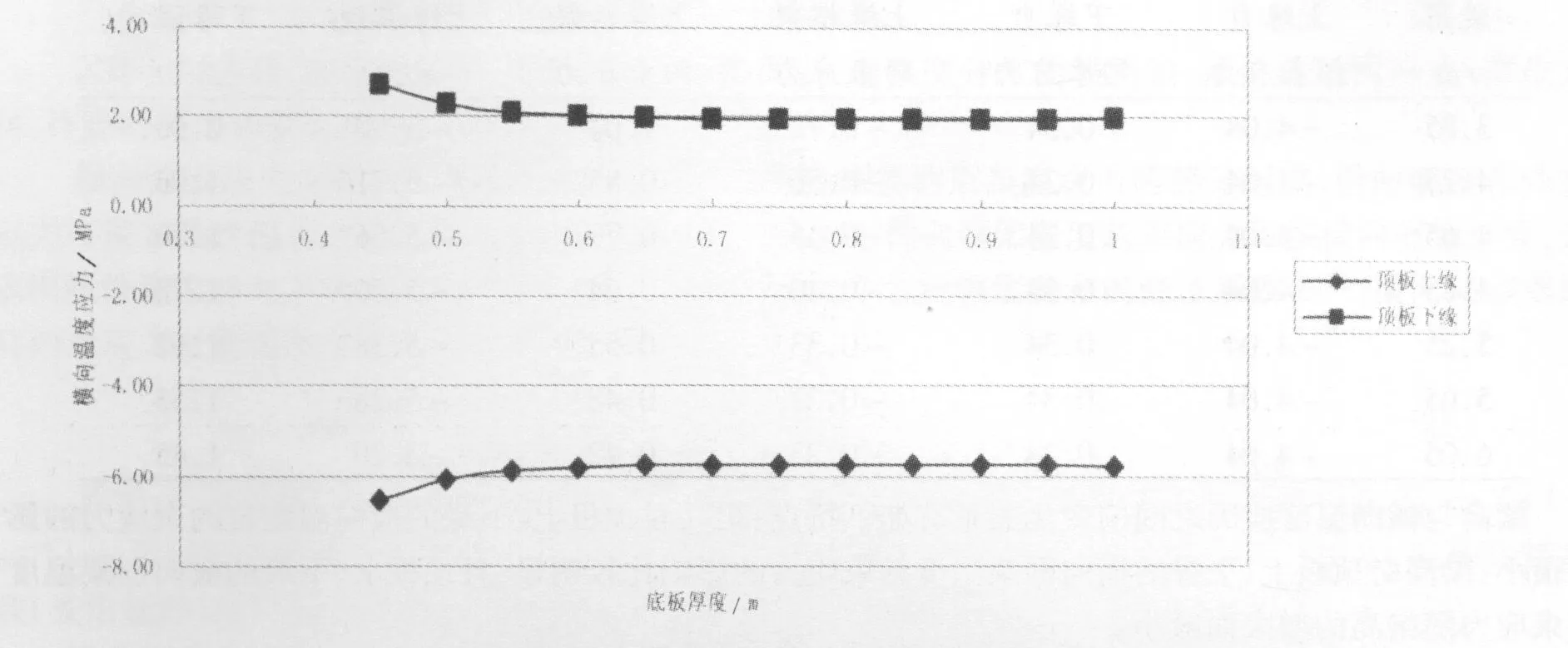
图5 横向温度应力随底板厚度的变化曲线图

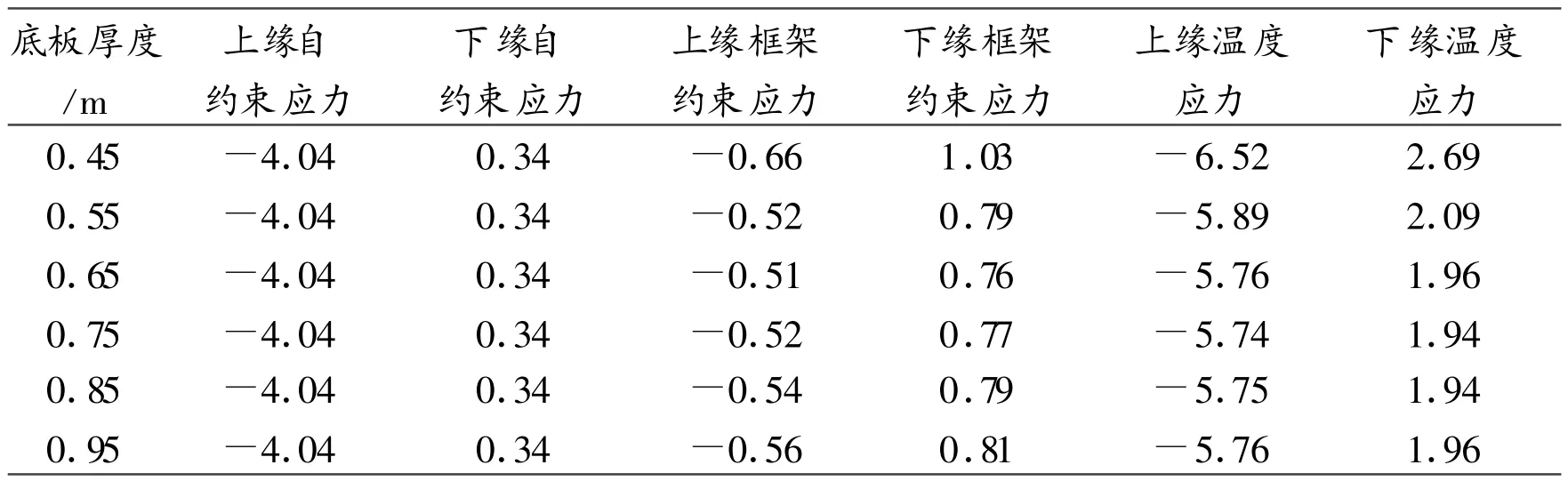
表3 横向温度应力随底板厚度的变化表/MPa

底板厚度与横向温度应力之间的变化关系有如下特点：底板厚度对顶板上、下缘的横向自约束温度应力的影响很小;当底板厚度小于0.65 m时,顶板上、下缘的横向框架约束温度应力随底板厚度的增大而增大;当底板厚度大于0.65 m时,顶板上、下缘的横向框架约束温度应力随底板厚度的增大而减小。

⑷横向温度应力随腹板厚度的变化关系见图6和表4。

表4 横向温度应力随腹板厚度的变化表/MPa

腹板厚度与横向温度应力之间的变化关系有如下特点：腹板厚度对顶板上、下缘的横向自约束温度应力的影响很小;当腹板厚度小于0.7 m时,顶板上、下缘的横向框架约束温度应力随腹板厚度的增大而增大;当腹板厚度大于0.75 m时顶板上、下缘的横向框架约束温度应力随腹板厚度的增大而减小。

根据以上图表,可得出以下结论：

⑴不管改变截面的哪个尺寸,横向温度应力在顶板下缘均为压应力,而在顶板上缘均为拉应力;梁高和顶板厚度对顶板上、下缘横向温度应力影响的比较简单,而底板和腹板对顶板上、下缘横向温度应力影响的比较复杂。

⑵横向温度自约束应力随梁高、底板厚度和腹板厚度的变化很小,而横向温度自约束应力随顶板厚度的增大而增大;横向框架约束温度应力随梁高、顶板厚度的增大而减小,横向框架约束温度应力随底板厚度和腹板厚度的变化在某些底板厚度和腹板厚度处的两侧呈现出截然不同的变化趋势。

⑶横向温度应力随梁高、顶板厚度、底板厚度和腹板厚度的变化较慢;横向温度应力随梁高和顶板厚度的变化有单调性,底板厚度和腹板厚度随横向温度应力的变化无单调性。

3 结语

⑴通过以上分析可知,有些截面顶板下缘的横向温度拉应力超出规范中混凝土的抗拉设计强度。铁路钢筋混凝土和预应力钢筋混凝土结构设计规范中C50混凝土规定的拉应力值为1.89 MPa,而这些截面的拉应力均超出该值。因此,在箱梁顶板的有必要设置横向预应力筋和温度钢筋来防止温度裂缝的产生。此外,在箱梁的腹板内侧和底板的上缘也有拉应力产生,在这两个部位也要采取措施防止温度裂缝的产生。

⑵本文采用现行铁路规范的温度曲线分析,但在实际桥梁的温度应力分析中应根据实际情况对其进行调整以获得更为准确的温度曲线。

⑶本文所分析的连续梁的温度分布曲线与规范中的温度分布曲线较吻合,且本文分析所得出的结论对其他类似桥梁的横向温度应力分析有一定的参考价值。

[1] 刘兴发.混凝土结构的温度应力分析[M].北京：人民交通出版社,1991.

[2] 范立础.桥梁工程[M].北京：人民交通出版社,2001.

[3] 项海帆.高等桥梁结构理论[M].北京：人民交通出版社,2001.

[4] TB 10002.1-2005.铁路桥涵设计基本规范[S].

[5] 王林,项贻强,汪劲丰.王建江各国规范关于混凝土箱梁桥温度应力计算的分析与比较[J].公路,2004(6)：76-77.

[6] 段凯,杨新华,杨文兵.用ANSYS软件计算桥梁结构的温度应力[J].四川建筑科学研究,2005(6)：55-59.

[7] 徐丰,王波,张海龙.混凝土连续箱梁温度应力对比分析[J].交通科技,2008(4)：10-12.

[8] 颉明军,惠卓.混凝土横竖向温度应力分析[J].华东公路,2007(12)：29-31.

[9] 夏修身.箱梁横向温度应力的研究[J].甘肃科技,2004(2)：97-98.

[10] 彭卫,施颖,张新军.预应力混凝土连续梁桥裂缝控制[J].混凝土,2002(1)：40-41.

[11] 刘惜君.变分法在桥梁结构温度应力计算中的应用[J].中外公路,2004(2)：10-13.