对称边界条件正交各向异性板的屈曲分析

王悦帆,张海峰,王彦宗

(西安建筑科技大学理学院,陕西西安710055)

薄板的屈曲问题是工程中比较常见的问题,若利用普通解法求解四边固定正交各向异性矩形板的屈曲问题比较困难,计算复杂,不易得到正确结果。但是如果利用傅立叶级数求解,求解起来就变的比较容易。

此法首先须将挠度假设为傅立叶级数形式,然后求出挠度各阶导数的傅立叶级数形式,再将其代入边界条件和屈曲的微分方程进行求解。为简化计算取1/4板为研究对象。对于四边固定的边界条件,可以取两临边简支,其中一边受有弯矩来求得一个挠度表达式,再将两个边的边界条件对调,求得另外一个挠度表达式,此时将两个表达式相加求得叠加解,从而求得临界力。

1 基本方程

正交各向异性板屈曲的微分方程

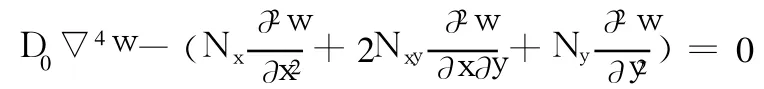
当不受纵向剪力,即Nxy=0时

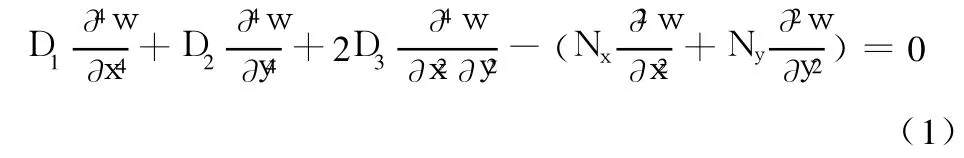
2 叠加解

在边界条件对称时(如图1所示),其解可分为:关于x=a/2与y=b/2双轴对称;关于x=a/2与y=b/2双轴反对称;关于x=a/2对称而关于y=b/2反对称;关于x=a/2反对称而关于y=b/2对称等4个问题。矩形板属于关于x=a/2与y=b/2双轴对称的问题。此问题给出两个叠加解。所有叠加解的傅立叶级数都取如下形式:

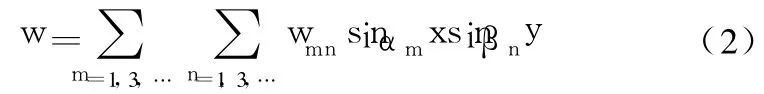
2.1 叠加解一

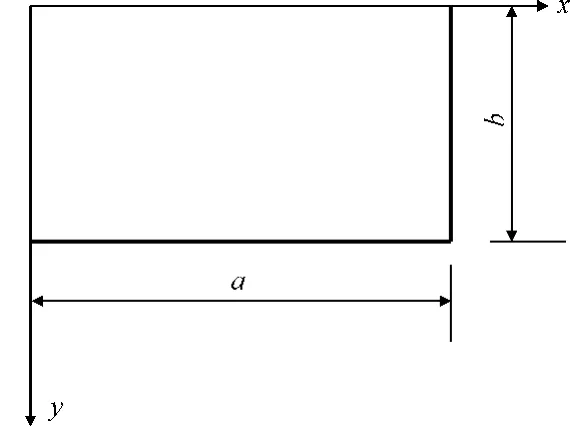
图1 边界条件对称板

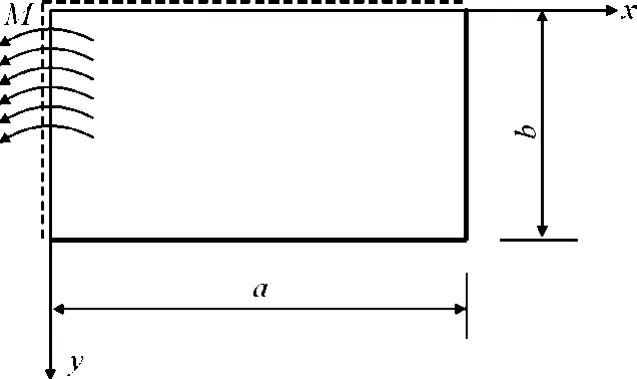
图2 叠加解一受力图

如图2所示,矩形板两邻边简支,且在x=0的边上受有弯矩。其边界条件为:

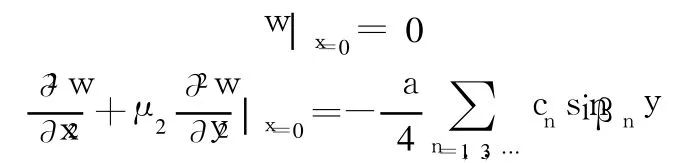
故x=0边上的边界条件可化为:

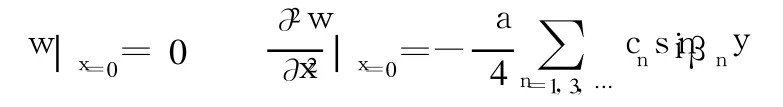
且y=0边上的边界条件为:

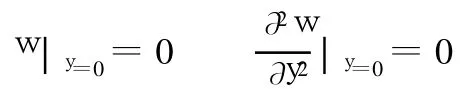
假设其三阶导数为以下形式:

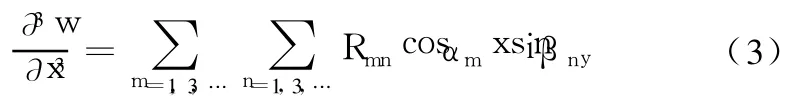
由傅里叶级数的相关性质计算求得:

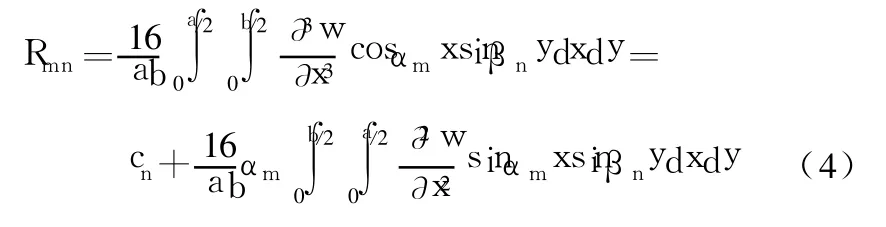
二阶导数可直接微分得到:

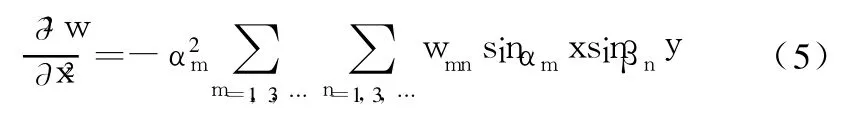
将式(5)代入式(4),得:

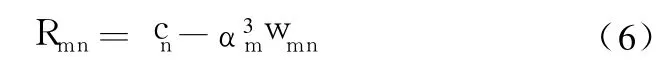
将式(6)式代入式(3)式得三阶导数:

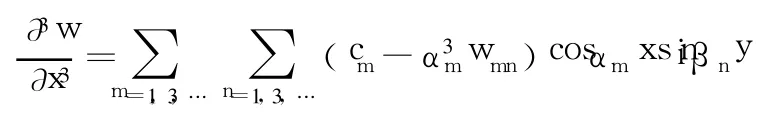
进而求得各阶偏导数:

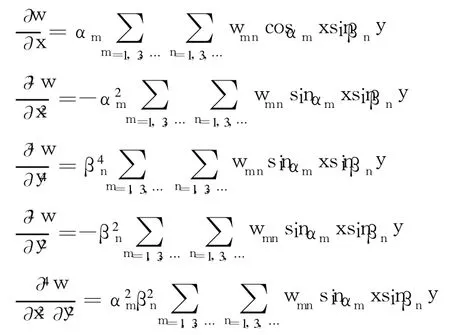
将以上各阶偏导数代入式(1)得:

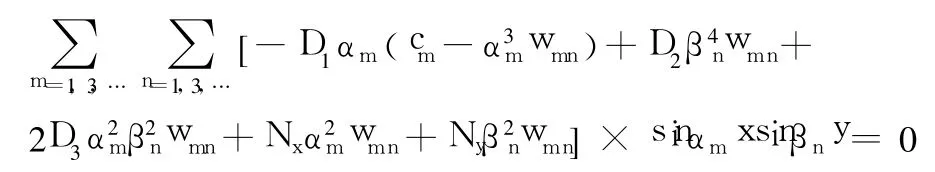
由于sinαmxsinβny≠0,故

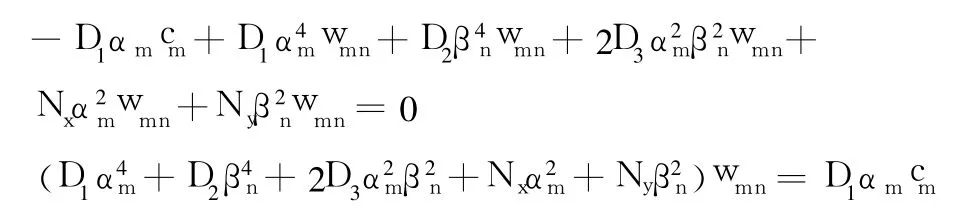
解得:

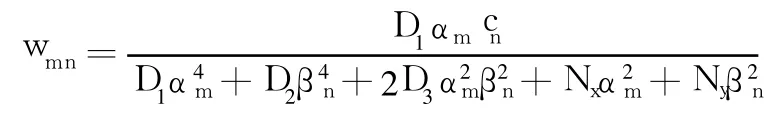
将其代入式(2),即可求得挠度表达式:

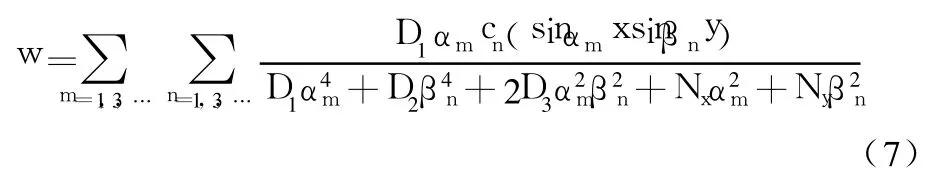
即得叠加解一。

2.2 叠加解二

如图3所示,矩形板两邻边简支,且在y=0的边上受有弯矩。其边界条件为:

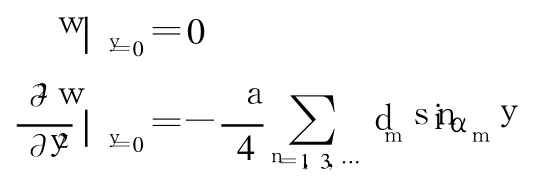
且x=0的边界条件为:

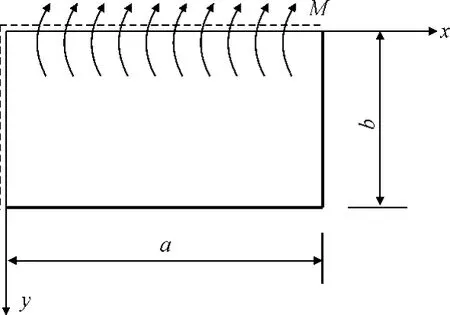
图3 叠加解二受力图

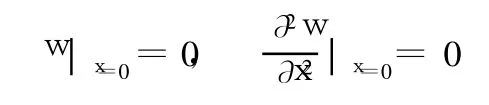
利用与叠加解一同样的方法可以得到:

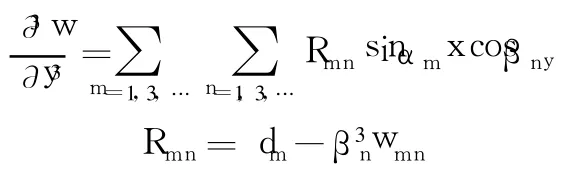
求得叠加解二的挠度表达式为:

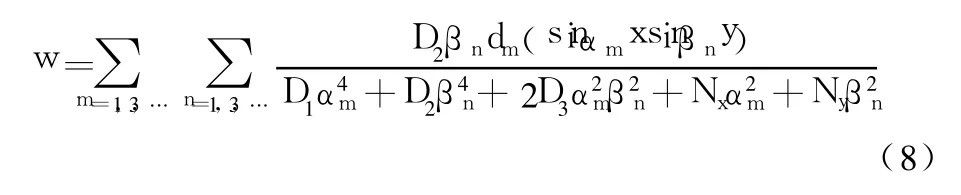
3 边界条件的叠加

将叠加解一与叠加解二相加,即式(7)与式(8)相加,求得两邻边简支且两边都受有弯矩时的挠度表达式,即

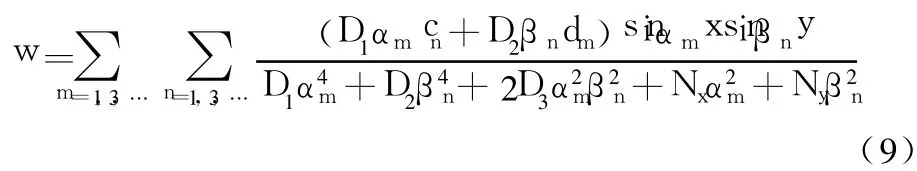
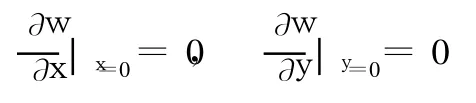
即可求出满足全部边界条件的解。

对式(9)求偏导数,得:

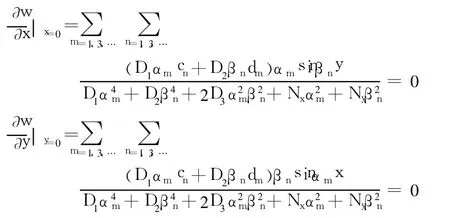
由上两式联立,只需求得方程组中的cn和dm,然后将求解得到的cn和dm回代到式(9)中便可最终求得挠度w表达式。

4 数值计算

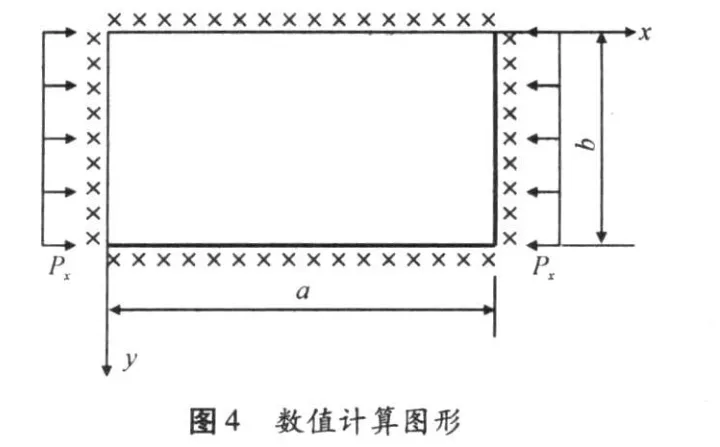
如图4所示的图形,四边固定的正交各向异性矩形薄板,它的两对边受有均布压力,在板边的每单位长度上为Px=1 kN/m,其中E1/E2=40,G12/E2=0.5,V12=0.25。

用matlab计算结果如表1

?

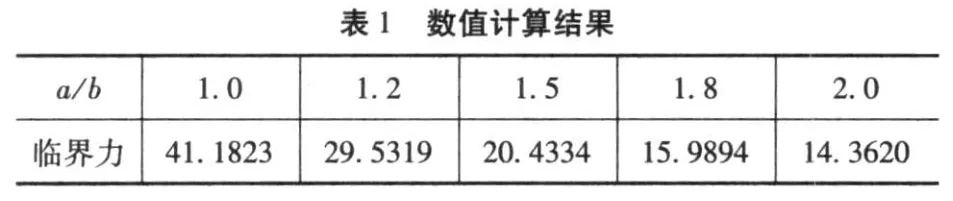
[1]徐芝纶.弹性力学[M].北京:高等教育出版社,1990

[2]王克林,刘俊卿,赵冬.平板的弯曲、振动和屈曲[M].北京:冶金工业出版社,2006

[3]王克林.带有自由边的矩形板的重三角级数解[J].西安建筑科技大学学报,1988,20(3):47-57

[4]黄义,王克林.反对称角铺层矩形板振动和屈曲分析[J].振动工程学报,1992,5(4):403-409.

[5]Kennedy JB,ASCE M,Prabhakaara M K.Combined-load buckling of orthotropic skew plates[J].Journal of engineering mechanics division,1979,105(1):71-79

[6]Wang C M,Liem K M,Xiang Y.Buckling of rectangular Mindlin Plates with internal line supports[J].JSolidsand Stuctures,1993,30(1):1-17