NaCl稀溶液结晶的分形形态研究

欧建文,李淑红,梁小平,王辅忠,李淑英

(天津工业大学a.纺织学院;b.理学院;c.材料科学与工程学院,天津300160)

1 引 言

传统的晶体形貌研究的是平衡态或近平衡态下的结晶形态,到19世纪末,对平衡态或近平衡态下的晶体形貌及其对称性研究已经相当成熟,并且在欧氏几何学框架下,整个几何晶体学理论体系已完全建立.然而100多年后,迅速发展起的一门分支学科准晶体学,给传统的经典对称理论带来猛烈冲击.同期,我国著名结晶矿物学家彭志忠教授率先提出将准晶态研究与分形几何学结合起来,并提出了准晶体的微粒分数维模型[1].此后,分形几何学与结晶学之间的结合迅速发展,为远离平衡态下的结晶形貌及集合体形貌的研究提供了强有力的数学工具.

分形(fractal)指的是一类极其破碎而复杂、但有其自相似性或自仿射性的体系,是20世纪70年代在法国人Mandelbrot创造性工作的基础上建立起来的一门新学科.分形理论在应用到晶体形貌研究之前已经在其他领域得到了广泛的应用,尤其受到数学、物理、化学乃至社会科学等各方面的广泛关注.

分形现象可发生在诸如电解沉积[2]、溅射凝聚、水溶液结晶、非晶态膜的晶化及黏性指延等远离平衡态的过程中.其中水溶液结晶因其实验装置简单、操作方便而成为被研究较多的实验系统之一.赵珊茸等在LiAlSiO4-SiO2体系中快速冷却结晶,形成在远离平衡态条件下的b-石英晶体形貌,找到一种具有Sierpinski铺垫分形图案的形态[3].葛副鼎等在不同的基底上喷洒生理盐水溶液,待其挥发后用扫描电镜观察了NaCl结晶的分形花样,指出有限扩散凝聚模型(DLA)是其成形机制[4].本文则研究了在玻璃基底下快速蒸发NaCl稀溶液所形成的分形花样,并对其成形机制和分形维数进行探讨.

2 实验方法

配制0.1 mol/L的NaCl稀溶液,滴在载玻片上并使液滴均匀铺开,放进100℃烘箱使水分迅速蒸发,得到NaCl结晶.在光学显微镜(UVG粒度分析仪)下观察结晶形态.在显微镜下取得不同放大倍数的照片,对结晶体逐步放大,选取成形良好的部分,视其边缘为二维平面中的一条折线,然后用不同尺度的线段去近似结晶体,求出它的分形维数.

3 Koch曲线及NaCl成形机制

Koch曲线是一类典型的分形曲线,如图1所示.传统Koch曲线的构造是把1条单位长度的直线段n=0等分成3段,将中间一段去掉,代之以互成60°的2条等长折线,形成1个生成元n=1,该曲线称为Koch曲线的第一阶生成.照此方法继续进行,一阶Koch曲线n=1构造出二阶Koch曲线n=2,以此类推,n→∞时呈现出一条有无穷多弯曲的Koch曲线.它具有严格的自相似性,即每个局部都与整体相似,并且在任意尺度下都反映了它的无限精细结构.传统Koch曲线也可以“随机生成”,只需在进行每次操作中令折线部分以一定概率“向上”或“向下”,经过n步后,得到看起来相当不规则的随机Koch曲线.与传统Koch曲线相比它依然具有无限精细结构,但严格自相似性变成了仅在统计意义下的自相似性.Mandelbrot自20世纪60年代起就注意到了自然界中广泛存在的不规则形体,提出用分形几何学来描述这些形态极不规则或极为支离破碎的几何现象,如山脉、云彩、海岸线等[5].

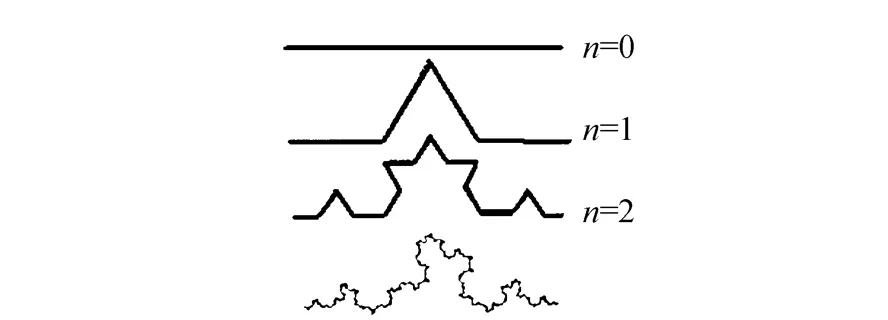
图1 Koch曲线和随机Koch曲线

图2为在玻璃基底上快速蒸发得到的NaCl稀溶液结晶形貌.从放大倍率较小的图2(a)中可以发现低浓度下的NaCl结晶花样并不像完整的NaCl结晶那样呈规则的立方晶体,而是一片结构紊乱、成形不规则、边界形状极其复杂的凹凸状结晶,该结构尺寸约为700μm,显然在统计意义下它具有明显的自相似性.随着显微镜倍率增大,原来的结构又呈现出许多尺度较小的一段段连续不规则曲线,形似随机Koch曲线,曲线尺度大致在120μm范围内,如图2(b)所示,此时图片仍然具有精细的结构.对图片再次放大,发现了大量成形不完整的NaCl小晶粒,它们基本上朝同一个方向生长,而缺失未成形部分则自组织起来顺次相互连接,排列规则而不是杂乱无章地堆积.不难发现,该结构中每个最小的组织都类似于Koch曲线的1个生成元,如图2(c)所示.由此推断,随着溶液的蒸发,不断有NaCl小晶粒成核析出,由于NaCl溶液浓度较低且蒸发速度快从而导致NaCl小晶粒结晶不完整形成了一个个微小的类似Koch曲线的生成元.生成元顺次相互连接,其间以一定概率“向上”凸或“向下”凹,从而形成一段段边界复杂的不规则的凹凸状曲线.显然这是一种从无序到有序的自组织现象,在远离平衡条件下自发形成了宏观的空间有序结构.实验参量如温度、浓度、基底表面的状态、蒸发速率等会强烈影响NaCl小晶粒的结晶、生成元的生长及生成元“向上”或“向下”的概率[6].

图2 NaCl稀溶液的结晶形貌

4 分形维数

分形维数是表征分形的重要参数,它可定量描述分形结构的自相似程度、不规则程度或破碎程度.有很多计算分形维数的方法,如相似维数、信息维数、关联维数、计盒维数和Hausdorff维数等.由于NaCl结晶弯曲复杂形似随机Koch曲线,本文采用改变观测尺度的方法求维数.

如图3所示,首先从高倍成像图片中选取成形良好且较具有代表性的结晶体作为观测对象.把该结晶体的一端作为起点,然后以此点为中心画半径为r的圆,把此圆与结晶体相交的点和起点用直线连结起来,再把交点重新看作起点,反复进行同样的操作,直至结晶体末端.这样即是采用长度为r的线段去近似凹凸弯曲的结晶体,记下所测得的线段总数N(r).改变基准长度r,重复上述操作,则N(r)也随着变化.

图3 改变观测尺度的方法求维数

由文献[5]可知,线段总数N(r)与基准长度r之间存在函数关系为

对上式两边取自然对数,得到

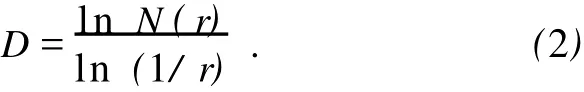
选取长短不同的3段结晶体,分别改变其基准长度r测得结晶体的线段总数N(r),所得数据见表1.

表1 基准长度r与结晶体线段总数取值N(r)

对N(r)与r取对数,然后对其双对数关系的离散点进行线性拟合,得到如图4所示的3条直线,其斜率分别为-1.21,-1.07,-1.08,求平均值得该结晶体的分形维数为1.15±0.06.显然,该结晶体维数与Koch曲线的维数1.26相近[6-8],并且离散点的线性相关性强,说明该结晶有显著的分形特性.

图4 维数计算的双对数坐标图

实验中,在同一块玻璃基底还发现有结晶成形良好的NaCl立方晶体[图2(a)中箭头所指]和结构较为致密的DLA凝聚体[图2(b)中箭头所指].完美的NaCl立方晶体是平衡态下的产物,DLA凝聚体葛副鼎等人已做详细研究,本文均不作讨论.

5 结束语

在远离平衡条件下,快速蒸发NaCl稀溶液得到结晶体.除发现有完整的立方晶体和DLA凝聚体外,还有形状复杂的凹凸状结晶.对该结晶体的成形机制进行研究,表明它符合随机Koch曲线,实验过程中温度、浓度、基底表面的状态、蒸发速率等对其有强烈影响.通过改变观测尺度的方法求得该结构分形维数是1.15±0.06.

[1] 彭志忠.准晶体的构筑原理及微粒分数维结构模型[J].地球科学,1985,10(4):159-174.

[2] 曹亦铮,徐碧漪,江洪建.变化电压下扩散限制电解沉淀过程对铜的分形维数的影响[J].物理实验,2007,27(9):3-7.

[3] Zhao Shan-rong,Tan Jin,Wang Ji-yang.A dendrite with“sierpinski gasket”fractal morphology in matt glaze of LiAlSiO4-SiO2system[J].Fractals,2003,11(3):271-276.

[4] 葛副鼎,朱静.NaCl溶液结晶时形成的枝叉状形态[J].电子显微学报,1998,17(6):744-747.

[5] Mandelbrot B B.The fractal geometry of nature[M].San Francisco:Freeman,1982.

[6] 张济忠.分形[M].北京:清华大学出版社,1995.

[7] 彭年,刘永顺.真实自回避行走中晶体生长界面结构的分形行为[J].岩石矿物学杂志,2007,26(5):449-452.

[8] 赵珊茸,王继扬,于光伟.数学在晶体形貌研究中的应用[J].人工晶体学报,2005,34(5):817-822.