阿贝成像原理和空间滤波实验的改进
袁 霞,王晶晶,金华阳
(深圳大学电子科学与技术学院,广东深圳518060)
1 引 言
阿贝成像原理和空间滤波是一个重要的普通物理光学实验,对于学生接受傅里叶光学空间频率、空间频谱、空间滤波等概念,熟悉阿贝成像原理,了解透镜孔径对成像分辨率的影响以及现代光学信息处理技术有十分重要的意义[1].
本文提出一种阿贝成像原理和空间滤波实验光路,可以简化现行的实验光路,操作简单,并可获得更好的实验效果.
2 阿贝成像原理
1873年,阿贝在研究显微镜成像问题时提出,在相干光照明下,透镜成像分两步完成,如图1所示.第一步是通过物的衍射光在透镜的像方焦面上形成1组衍射斑,这些衍射斑称为物的空间频谱;第二步是各衍射斑发出的球面次波在像平面上叠加,形成原物的像,即空间频谱的再组合.由阿贝成像原理可知,可以通过改变空间频谱来改变图像.
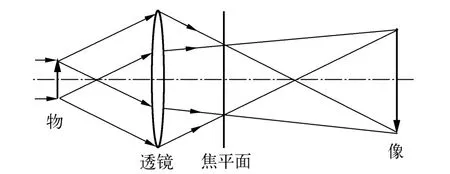
图1 阿贝成像原理
根据阿贝成像原理,阿贝-波特实验装置与图1相同[2-4].以光栅为物,将激光器发出的光扩束准直后入射到光栅平面,在透镜的后焦面得到其空间频谱,在较远的像平面得到光栅的像.实验内容有[4-5]:观察并测量光栅的频谱分布,计算各衍射点的空间频率;在频谱面上滤波,观察像面上图像变化;以透明字和网格(或正交光栅)重叠作为物,做低通滤波实验.
3 实验原理
改进的光路如图2所示.由激光器发出的光经过扩束后入射到物平面P1,P1置于傅里叶变换透镜的前焦面,可以证明:频谱面为光源的共轭像面,并且频谱面上的空间频率与位置坐标的关系与用平行光照射物平面时二者的关系相同,为证明如下.

图2 改进的阿贝成像原理和空间滤波实验光路图
如图3所示,单色点光源S位于光轴上,与透镜的距离为u.物平面P1位于透镜的前焦面,复振幅透过率为t(x1,y1).点光源的共轭像面Pi与透镜的距离为v.在近轴条件下,由S发出的

图3 推导空间频率与位置坐标的关系
单色球面波在物的前表面的场分布为

经过物平面P1后的光场为

按照菲涅耳衍射公式,光波到达透镜平面的场分布为

上式略去了常数相位因子.忽略透镜孔径的衍射作用,通过透镜后的场分布为

再次使用菲涅耳衍射公式,同样忽略常数相位因子,到达观察面的光场分布为
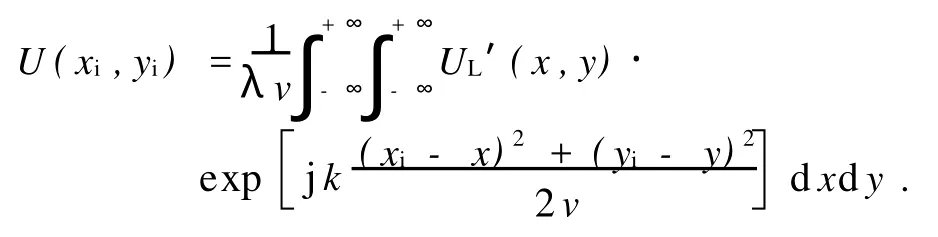
将前面各式代入上式得:

将指数项合并得:

其中:
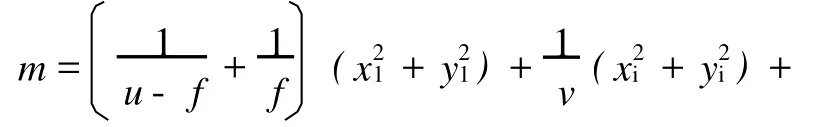
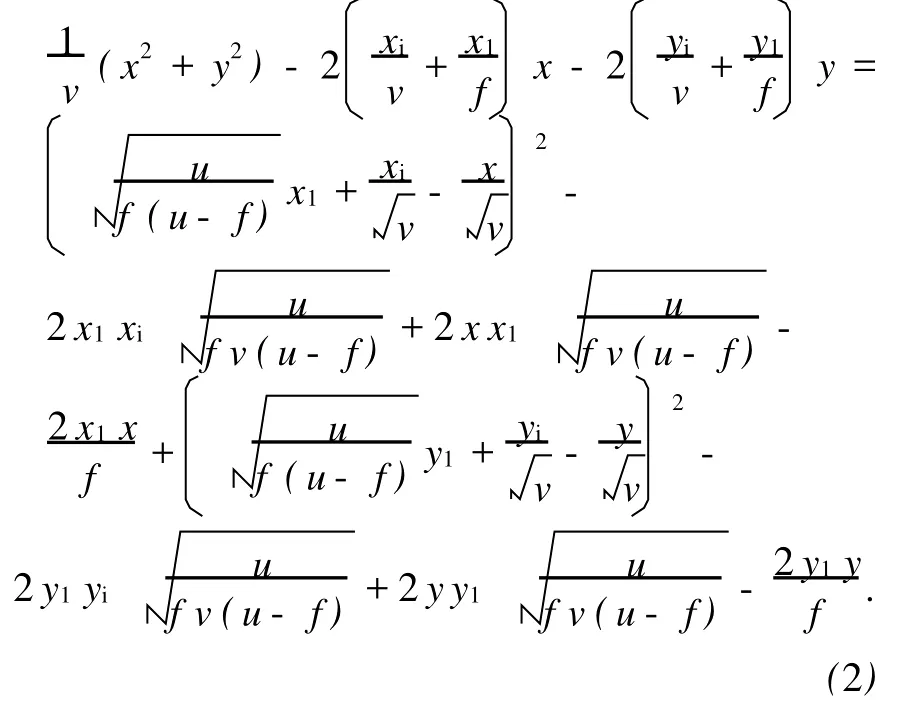
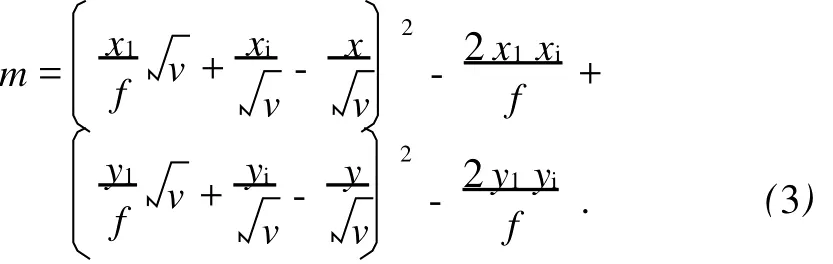

利用(4)式,

将(5)式代入(1)式:
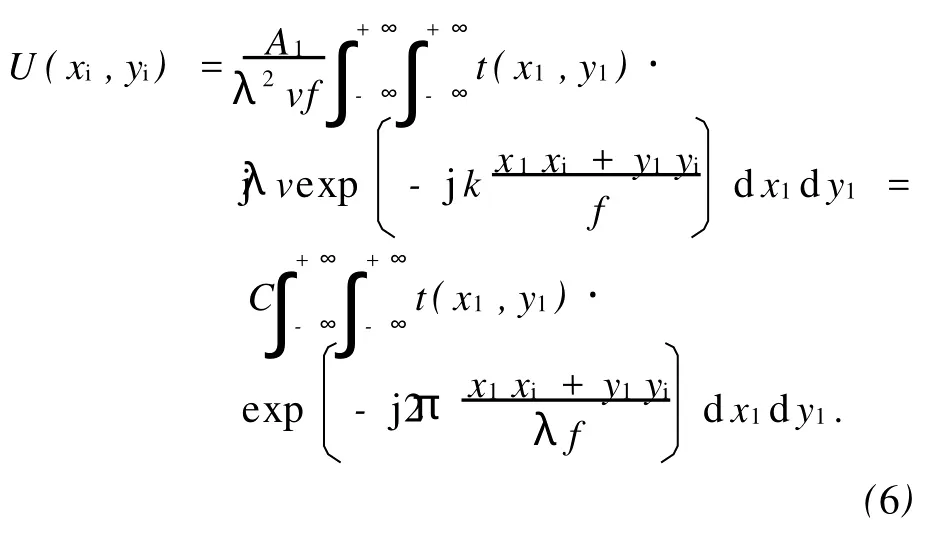
式中C为常数.由此可见,光源的共轭像平面的光场分布是衍射物体的复振幅透过率的傅里叶变换,并且像平面上空间频率与位置坐标的关系为

4 实 验
实验采用DH-LD650-5A型半导体激光器(5 mW,650 nm),焦距为15 mm的平凹透镜作扩束镜,空间频率为100 mm-1的一维光栅为物,透镜L焦距为120 mm,光栅置于成像透镜的前焦面上.
在频谱面上测量第1,2,3级衍射点与0级衍射点的距离x,并计算空间频率,结果见表1.
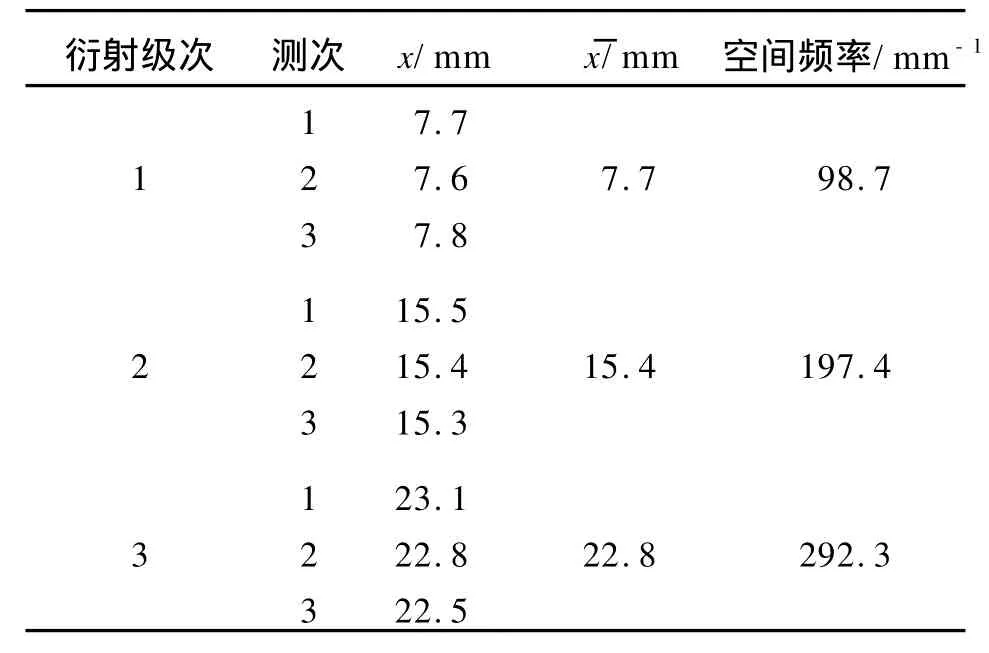
表1 实验结果
由表1计算得到的基频分量为98.7 mm-1,与标准值100 mm-1相比,相对偏差为1.3%.
在做低通滤波实验时,为了使像有较大的放大倍数同时有足够的光强,应将由透明字与正交光栅重叠组成的物尽量贴近扩束镜.在相同的条件下,因为减少了准直透镜,改进光路的物像间距可以比原光路的物像间距大,从而能获得更大的放大倍数,像面也比原光路更明亮,实验效果优于原光路的效果.
5 结束语
本文从理论上证明:物平面置于傅里叶变换透镜的前焦面时,频谱面为光源的共轭像面,并且频谱面上的空间频率与位置坐标的关系为ξ=实验也证实了该结论.根据此结论改进的阿贝成像原理与空间滤波实验简化了光路,减少了一次透镜的共轴调节,减小了操作误差,使光路调试简单、方便,实验结果更加准确,实验效果更好.
[1] 李芳菊,董康军.利用阿贝成像原理制作低频全息光栅[J].物理实验,2008,28(5):37-38.
[2] 赵凯华,钟锡华.光学(下册)[M].北京:北京大学出版社,1984:75-77.
[3] 苏显渝,李继陶.信息光学[M].北京:科学出版社,1999:207-208.
[4] 陈怀琳,邵义全.普通物理实验指导(光学部分)[M].北京:北京大学出版社,1990:268-269.
[5] 陈怀琳,马静帘.阿贝成像原理和空间滤波——一个有关傅里叶光学的教学实验[J].物理实验,1980,(2):22-26.

