拟合法测量高斯光束的束腰半径

黄水平,郭旭东,张飞雁,叶 忠

(宁波大学理学院,浙江宁波315211)

1 引 言

随着激光技术的广泛应用和不断发展,对高斯光束的研究和测量成为一个重要课题.对高斯光束束腰半径的测量曾有过多种方法,如针孔扫描法、狭缝扫描法[1]、刀口扫描法[2-3]、CCD法、扫描Ronchi刻尺法[4-5]和激光散斑法[6]等.传统的针孔法(狭缝法或刀口法)通过寻找光功率分别为2个特殊值时针孔(狭缝或刀口)所在的位置,来获得束腰的尺寸,测量数据点单一,通常难以准确找到所需的针孔(狭缝或刀口)位置,容易产生较大的随机误差;CCD法测量中,通常必须对测量光束进行衰减以避免CCD的饱和,而衰减装置的引入会导致一定程度的光斑变形;Ronchi刻尺法既需要制作高精度的特殊光栅,又需要有1台电机带动光栅做连续的匀速移动,以找出透射光强的极大值和极小值;激光散斑法不仅需要CCD和计算机与相关软件,测量误差也相对较大.本文从高斯光束的性质出发,根据其横向光强分布,采用2种不同的拟合方法(多孔径光功率拟合法和多点光强拟合法)测量高斯光束束腰半径,得到了较好的结果.

2 测量原理

根据高斯光束的性质,在z处横截面内,高斯光束的场振幅分布可表示为[7-8]

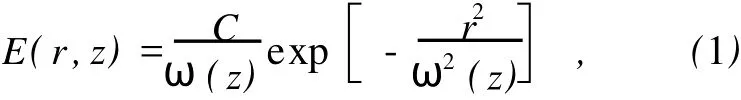
式中:r为考察点离光斑中心的距离,C为常数因子,ω(z)为z处横截面上的光斑半径,即振幅降为中心值的时的半径.高斯光束的光斑半径ω(z)随坐标z(即传播方向的坐标)按双曲线规律变化,即:

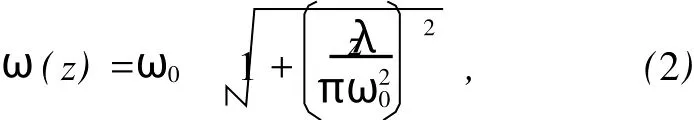
式中ω0为束腰半径(即光斑最小时的光斑半径),λ为激光波长.

在高斯光束束腰处,横截面内的光强分布为

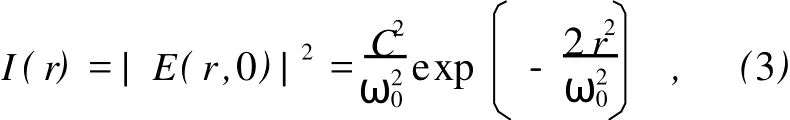
对光强归一化后有

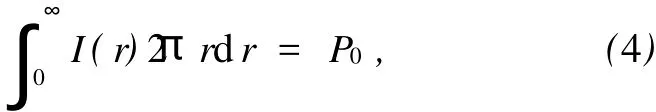
从而得出

其中P0为高斯光束的总功率.

因此,高斯光束束腰处的光强分布表达式最终可写为

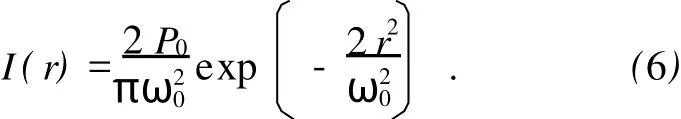
实验中如测出多个位于不同r处点的光强I(r),便能利用(6)式拟合出P0和束腰半径ω0.

若在激光束的束腰处加一小孔半径为R的小孔光阑(小孔中心与光束中心重合),则从小孔中透过的光功率为

如测出不同孔径光阑的光功率,利用(7)式也可拟合出P0和束腰半径ω0.

3 实验装置

图1为实验装置示意图.为减少氦-氖激光器输出光强不稳定带来的误差,实验中采用了双光路测量.入射激光束通过分光镜一分为二,一束用于束腰测量(测量光束,由硅光电池1测量),一束用于记录激光器光功率的变化(参考光束,由光电池2测量),以测量光束的读数和参考光束的读数之比作为各不同孔径的相对功率或各不同点的相对光强.两硅光电池(连同前面的小孔光阑)分别装在2个三维调节架上,以便于对其位置进行较精密的调节和较准确的读数.图中扩束镜用于改变高斯光束的束腰位置并对高斯光束进行扩束,以方便测量.

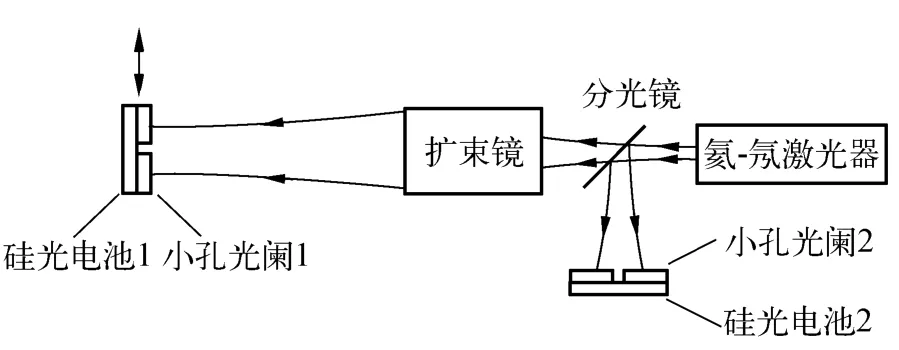
图1 测量装置示意图

利用(6)式进行多点光强拟合时,采用足够小的针孔,用透过针孔的功率来代表光斑某点的光强.实验时让针孔(连同硅光电池)沿着与高斯光束轴线垂直的方向移动,可得到不同半径r处的光强.本实验中,所用针孔的直径为0.15 mm.

利用(7)式进行多孔径光功率拟合时,通过改变探测器前光阑的大小,得到不同的光电流,用理论公式拟合所得的实验曲线,得到了高斯光束的束腰半径.如此,避免了传统扫描测量方法中由于单数据测量存在的误差.另外,通过测定透过激光能量与光阑大小的关系来确定束腰半径,在实验方法上更简单,操作上更方便.

此外,从光电池的光照特性可知,在光电池的特性参数中,与入射到光电池上的光强或光功率成线性关系的是光电池的短路电流[9],而只有在外接负载电阻(包括仪表内阻)RL≪Rd(Rd为光电池内阻)时,才可认为接近短路.Rd一般属低值范围,其大小会随光强的增加而急剧下降.为保证测量具有较好的线性关系,实验中,光电流测量电路中的负载应控制在50Ω以内.

4 测量结果

表1为用图1装置测出的不同r点的相对光强大小.由表1可以看出,测量起点并没有选在光束的中心,这样做更方便于实际操作.此时拟合公式(6)应改为高斯函数的一般形式:

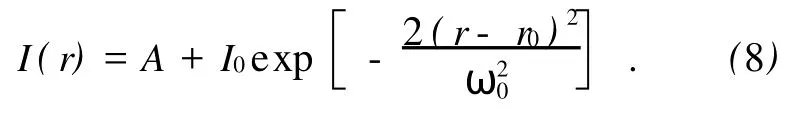
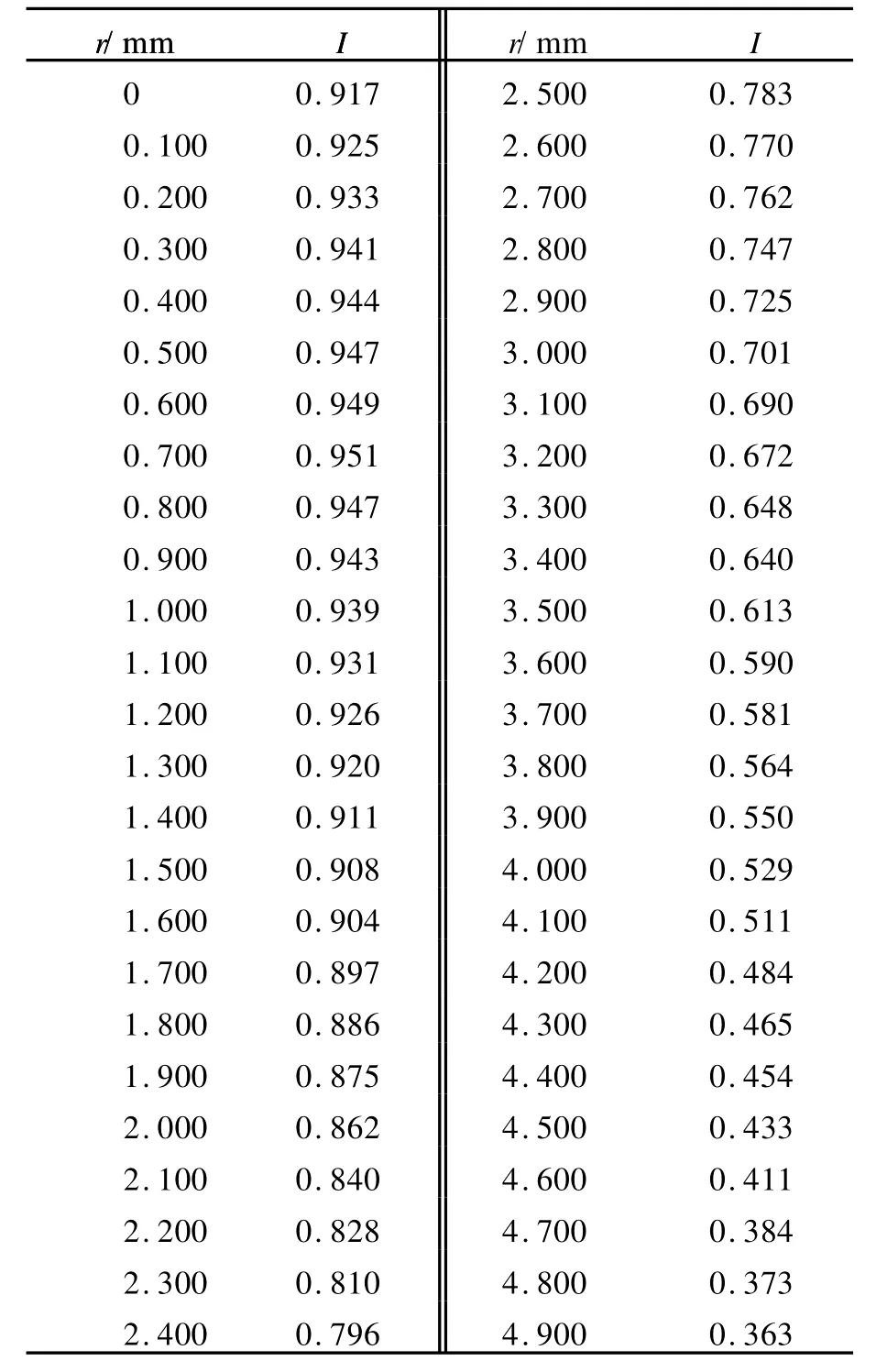
表1 不同位置点r的相对光强I测量结果

采用(8)式取代(6)式拟合数据的好处是可减少确定光束中心时由于不准确而带来的误差.

图2为利用(8)式对表1数据的拟合结果.从图中可以看出,拟合曲线与测量数据能很好吻合.拟合出的束腰半径为ω0=6.364 mm.

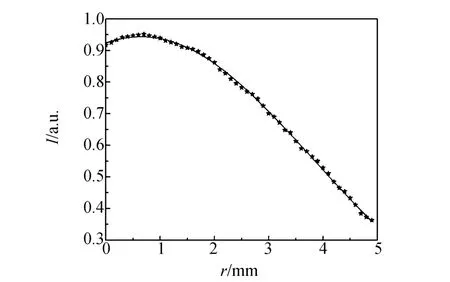
图2 不同位置点的光强拟合曲线

表2为不同小孔光阑透过光功率的测量结果.图3为用(7)式对表2数据进行拟合的结果.从图3可看出,拟合曲线与测量数据符合得较好.拟合出的高斯光束束腰半径为ω0=6.392 mm.可以发现,两种拟合方法所得结果基本一致.

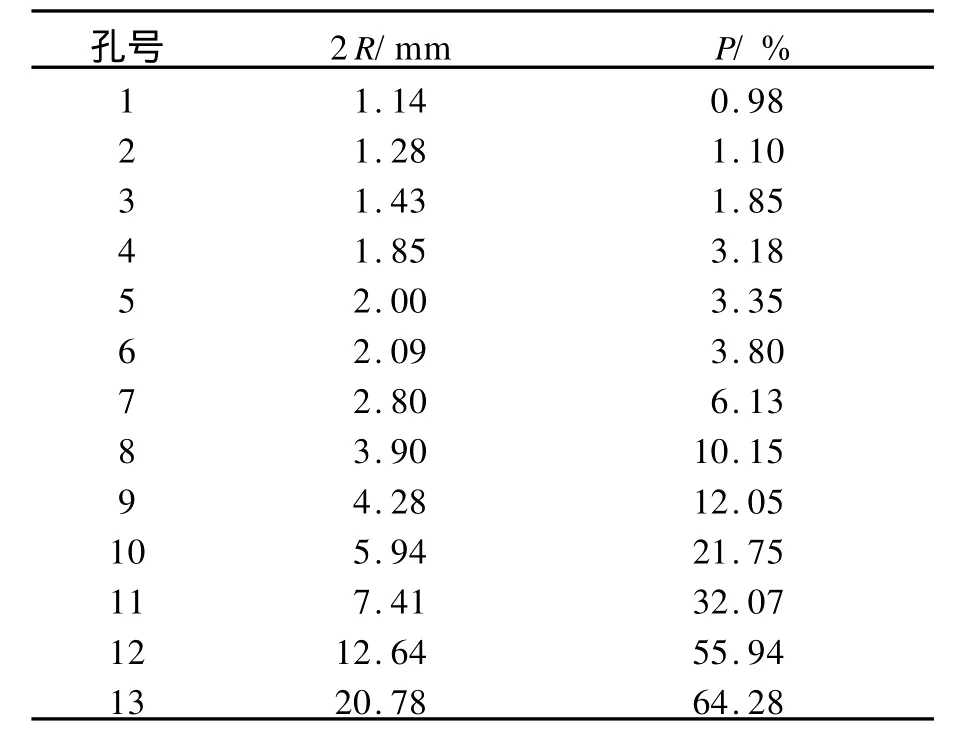
表2 不同小孔光阑对应的光功率

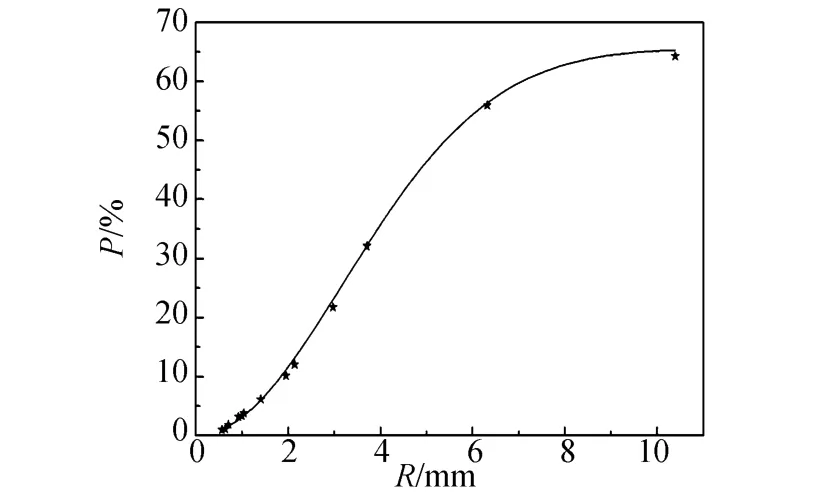
图3 不同小孔光功率的拟合曲线

5 结束语

在分析传统测量方法不足的的基础上,从高斯光束的横向光强分布特性出发,建立了小孔光阑透过功率与孔径的关系式.采用2种不同拟合方法对高斯光束的束腰半径进行了测量.为减小激光器功率不稳定带来的不利影响,实验中采用双光路进行测量.结果表明,用拟合法测量高斯光束的束腰半径不仅合理,而且可行,能有效防止传统孔径法或针孔法等由于测量数据单一而可能出现的较大误差.

[1] 蔡伯荣,魏光荣.激光器件[M].长沙:湖南科学技术出版社,1981:38-39.

[2] 熊小华.刀口法测量高斯光束腰斑大小实验设计[J].南京航空工业学院学报,2000,14(3):1-3.

[3] Bilger T H,Habib R.Knife-edge scanning of an astigmatic Gaussian beam[J].Applied Optics,1985,24(5):686-690.

[4] Cherri A K,Awwal A A S,Karim M A.Generalization of Ronchi,sinusoidal,and triangular nulings forGaussian-laser-beam-diametermeasurements[J].Applied Optics,1993,32(13):2 235-2 242.

[5] Dickson L D.Ronchi ruling method for Gaussian beam diameter[J].Optical Engineering,1979,18(1):70-75.

[6] 姚昆,侯碧辉,张增明,等.散斑位移法测高斯光束的空间分布[J].强激光与粒子束,2000,12(2):141-144.

[7] 邱元武.激光技术和应用[M].上海:同济大学出版社,1997:42-57.

[8] 王涛,吴福全,马丽丽,等.尼科耳棱镜对单模高斯光束光强分布的影响[J].物理实验,2008,28(4):1-5.

[9] 唐爽,岑剡.利用硅光电池测量硅单晶半导体材料的禁带宽度[J].物理实验,2008,28(11):6-8.