声速测量实验原理讨论
王开圣,赵志敏,刘小廷
(南京航空航天大学理学院,江苏南京211100)
1 引 言
测量空气中声速有多种方法,其中之一为驻波共振法,其实验电路见图1,大学物理实验指导书对驻波共振法测声速原理一般作如下描述,S1和S2分别为超声波发射与接收压电探头,S1发出的声波以平面波的形式传播,在S2表面发生反射,两探头间的入射波和反射波相互干涉,当S1与S2的间距满足半波长的整数倍时,出现驻波共振现象,形成振幅最大的驻波,此时S2表面为驻波波节,声压最大,压电探头输出的电信号最大.实验时移动S2,系统经历一系列的驻波共振状态,信号幅度周期性地变化,任意2个相邻的信号极大值所对应的S2移动距离为半波长,此距离由游标卡尺测得.实际上,由于传播过程中声波的衰减以及界面的反射损失,入射波和反射波的振幅不相等且不断变化,这样的波相干叠加,显然不符合形成驻波的条件,合成波不是理想的驻波,文献[1]等对此已有阐述,实验中观测到的信号衰减现象以及信号极小值不为零等问题,驻波共振原理都无法做出解释.文献[2-4]在考虑声波吸收衰减的条件下,用平面波理论描述声波,得到了信号幅值仍以半波长为周期随探头间距变化,与驻波共振原理的结果一致.但考虑了声波吸收的平面波理论仍不能解释清楚实验所观测到的信号衰减规律.由声学理论可知,实验用的圆形压电探头产生的声波并不是平面波,而是活塞波,其在远场区以球面波的形式传播,在传播过程中除了吸收衰减,还存在波阵面扩散造成的衰减.为合理解释信号衰减规律,本文设声波以球面波形式传播,同时也考虑到空气对声波的吸收衰减,研究接收声压的变化规律,并用数值分析法把用平面波与球面波方法所得到的声压衰减规律进行比较.
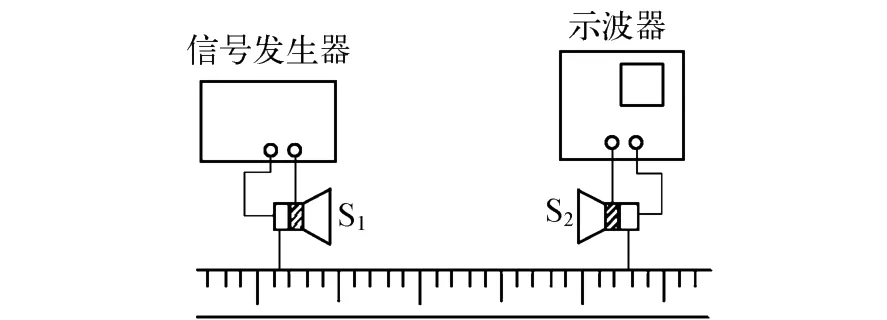
图1 声速测量实验电路
2 接收探头表面声压的推导
声速测量实验时,示波器上信号幅值的大小取决于接收压电探头处的声压,两者成正比,因此,以下分析接收声压随探头间距的变化规律.
如图1所示,由探头S1发出的超声波向右传播,到达接收探头S2表面发生反射,成为逆向波,逆向波向左传播到S1表面再次发生反射,成为正向波,如此往复,S1与S2之间有无穷多个正向波和逆向波,S1与S2间的声场是这些波干涉叠加的总效果.设S1与S2之间的距离为L,用与分别代表各次正向波和逆向波在S2表面产生的声压,求解声压过程如下.
2.1 声波以球面波形式传播时的接收声压
设发射探头S1表面的声压为

P0为探头表面发射声压振幅,ω为振动圆频率.
以S1的中心为x轴坐标原点,根据声学理论,声波在远场区以球面波形式传播,其S1与S2在连线上以声压表示的波动表达式为[5]

其中S为探头发射面的面积,k=2π/λ为角波数,λ为波长.
设空气对声波的吸收系数为α,式(2)修正为
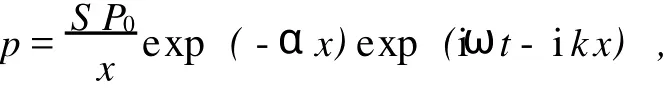
令x=L,得一次正向波在接收探头S2表面的声压为

为简化推导过程,令

将式(1)和(4)代入式(3),简化为

一次正向波在S2处发生反射,形成逆向波,反射面两侧介质为空气和铝,其声压反射率可按式(6)计算[6]

其中,空气的特征阻抗Z1=4×102kg·m-2·s,铝的特征阻抗Z2=17.1×106kg·m-2·s.
计算得γ=0.999 95,反射率为正数表明反射时声压的相位不变,只是振幅有微小的损失,则一次逆向波在S2处的声压为
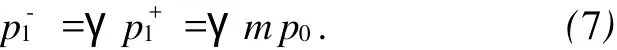
按照与求解一次正向波同样的方法,可求出一次逆向波到达S1处产生的声压为γm2p0.
一次逆向波经S1反射,形成二次正向波,其在S1处的声压为γ2m2p0,到达S2处的声压为

二次正向波在S2处反射,形成二次逆向波,在S2处的声压为

依次类推,其余各正向波和逆向波在S2处的声压分别为

这无穷多个波叠加后,S2处的总声压为


将式(5),(7)~(11)…代入式(13)可得

将式(1)和(4)代入式(14)得接收探头处总声压为
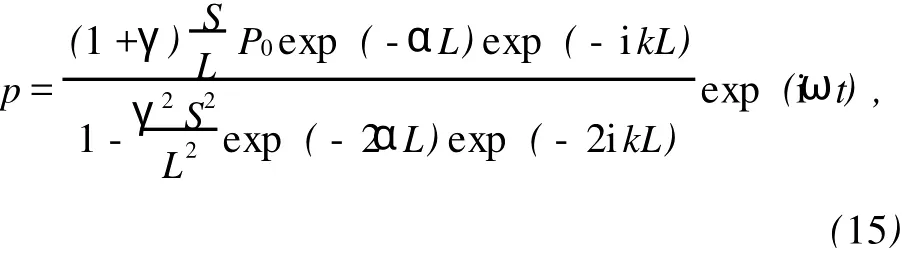
从式(15)求出声压p的模

当cos(2kL)=1,即L=nλ/2(n为整数)时,式(16)分母有极小值,则声压幅值达到极大值:
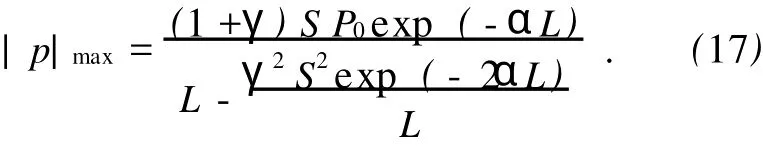
表明当探头间距为半波长的整数倍时,接收声压达到极大,极大值呈现以半波长为周期的变化规律.当cos(2kL)=-1,即L=nλ/2+λ/4时,式(16)分母有极大值,则声压幅值达到极小值

声压极小值以半波长为周期变化.
2.2 声波以平面波形式传播时的接收声压
用与2.1中同样的推导方法,可求出声波以平面波形式传播时的接收声压、声压极大值和极小值.类似推导过程文献[2-4]中也给出,不再赘述.结果如下:
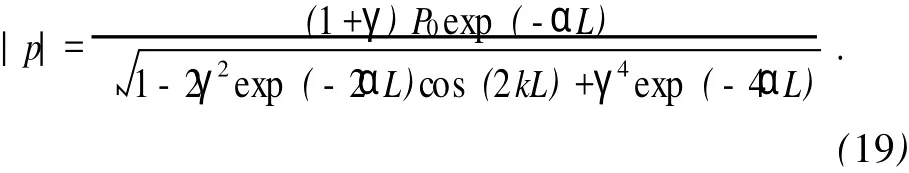


声压极大值和极小值以半波长为周期变化.
3 声压幅值衰减规律的讨论
从式(17),(18),(20),(21)的解析结果可看出,考虑空气吸收的球面波理论和空气吸收的平面波理论都给出了声压按半波长的周期性变化规律,与驻波共振理论相一致,在这一点上三者有共性,但在描述声压衰减规律时出现了差异.
驻波共振理论认为声波无衰减,声压极大值不随距离变化,极小值为零,显然与实验结果相悖.而从平面波理论的式(17)和(18)及球面波理论的式(20)和(21)可看出,声压极大值都随距离增加而衰减,极小值都不为0,似乎都与实验现象一致.但通过Matlab软件,用数值方法模拟接收声压随距离的变化情况,即将式(16)~(21)图示化,进行比较后发现2种理论处理方法存在差异.
根据实验仪器的技术参数确定模拟量,声波频率f=35 kHz,探头直径38 mm,声压反射率γ=0.999 95,常温下空气吸收系数α[7]为2.94~3.99×10-11f2,模拟时取3.5×10-11f2.模拟结果如图2和图3所示.
图2显示了平面波条件下声压衰减情况,声压极大值随探头间距增大而出现一定程度的减小,与实验观察到的现象较一致,但极小值非常小,极大值与极小值相差数百倍,这与观测到的实验现象明显不相符.
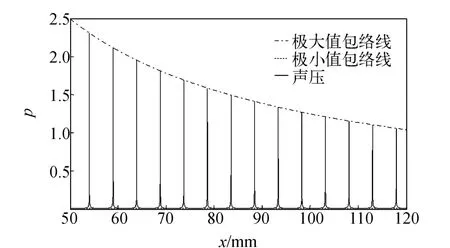
图2 平面波条件下声压衰减规律
图3显示了球面波条件下声压衰减情况,声压极大值随探头间距增大而减小,衰减速度比平面波要快,这更接近测量结果;极大值与极小值的差值不像平面波那么大,这与测量结果相近.

图3 球面波条件下声压衰减规律
从上面分析可看出球面波表示的声场比平面波更接近实际情况,因为平面波方法仅考虑了声波的吸收衰减,而低频超声波在空气中吸收系数较小,这使得声波衰减速度慢,这样入射波与反射波的振幅相差不大,干涉叠加后,声压极小值虽然不为零,但会小于极大值.而球面波理论处理时,不仅考虑了声波的吸收衰减,而且考虑了波阵面扩散所引起的扩散衰减,所以声波的衰减速度比平面波要快,入射波与反射波的振幅相差较大,这样干涉叠加后,声压极大值与极小值的差值不会像平面波那样大.
4 结 论
通过用平面波方法以及球面波方法分析发射和接收探头之间的声场,得到以下结果:
1)尽管由于空气对声波的吸收衰减,波阵面的扩散衰减及界面反射损失,探头间声场不是理想驻波,但任意2个相邻信号极大值或极小值所对应的探头移动距离仍为半波长,与理想的驻波共振理论相一致,利用这种周期性可测量波长.
2)用球面波处理方法得到的声场比较准确,能更全面地解释声速测量实验中观测得到的现象,有助于理解实验中的声波衰减问题.
[1] 陈洁,苏建新.声速测量实验有关问题的研究[J].物理实验,2008,28(6):31-33.
[2] 郑庆华.声速测量实验的探讨[J].大学物理,2007,26(9):31-33.
[3] 胡险峰.驻波法测量声速实验的讨论[J].物理实验,2007,27(1):3-6.
[4] 赵新闻.声速测定中“驻波共振”条件的讨论[J].物理与工程,2002,12(3):11-18.
[5] 罗斯J L.固体中的超声波[M].北京:科学出版社,2004:277.
[6] 杜功焕,朱哲民,龚秀芬.声学基础[M].南京:南京大学出版社,2001:203.
[7] 许肖梅.声学基础[M].北京:科学出版社,2003:246.

