“0.618”法、Fibonacci法、抛物线法搜寻复摆周期极值点
刘向远,梅忠义,张穗萌
(1.皖西学院数理系,安徽六安237012;
2.合肥工业大学电子科学与应用物理学院,安徽合肥230009)
1 复摆模型
图1所示的模型是一种钟摆式复摆,当支点确定后,整个系统的质心可以随图中摆锤M的移动而变化.O点是整个装置的支点,O点以上部分为菱形支架,O点以下为带有刻度的直杆,其长度为L,杆上套有可移动的圆柱形摆锤M并以杆为对称轴,其质量为m,半径为R.通过调节摆锤M,当摆锤质心在B点距支点O为x0时,系统质心正好位于O点,此时,系统的转动惯量为I0.

图1 可变质心复摆模型
设摆锤质心在直杆上离开支点O的距离为x,当摆角小于5°时,复摆的周期公式为
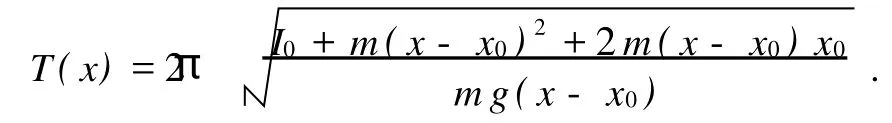
能够证明T随x在(x0,∞)区间内变化存在极小值[1-2].对于不同质量m的摆锤,T随x变化的曲线如图2所示.在实验室条件下,如果未知此复摆的有关参数,要求快速、准确地寻找到它的极值点位置,可以采用一维精确搜索法来优选极值点.

图2 复摆周期T随x变化的曲线
2 用“0.618”法、Fibonacci法、抛物线法搜寻复摆周期极值点的实验方法
2.1 “0.618”法与Fibonacci法的基本思想
“0.618”法和Fibonacci法属于一维精确搜索法中的分割法,这2种方法的基本思想是[3]:在已知的初始区间[a0,b0]内,选定两个新的内点ak,bk,然后测出ak和bk对应的周期Tk和Tk′,并比较Tk与Tk′的大小,采取舍大取小的原则,舍去Tk与Tk′中对应的较大的内点以外的点,保留较小的内点,由此建立新的搜索区间,在新的搜索区间内再选取新的内点,重复以上的比较过程.按照这样的步骤重复循环,逐步缩小搜索区间,直到达到所要求的区间范围,并且取最后区间端点的平均值作为极小周期点的位置.
2.2 “0.618”法与Fibonacci法的不同点
“0.618”法与Fibonacci法在确定新的内点时有区别:“0.618”法确定新内点所取区分系数r=0.618,为恒定值.因此

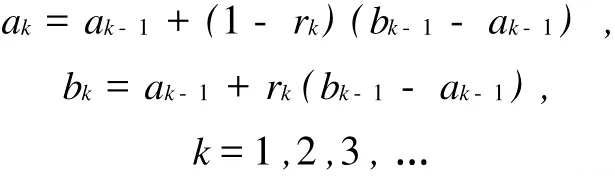
这样,两种方法在缩小搜索区间上有所不同,“0.618”法每次缩短搜索区间的长度为38.4%,而Fibonacci法缩短搜索区间的长度由1-rk来确定,是变化的.
另外,Fibonacci法中的区分系数还必须根据要求缩小的区间长度来确定Fn.假设要求将极值点xmin缩短到长度为l的区间内,则

此时,取Fn在Fibonacci数列中满足条件的最小整数,并由此确定n值[4].当区分系数为时,应该加上或减去很小的数值,本实验减去0.02.
2.3 搜寻复摆极值点的抛物线法
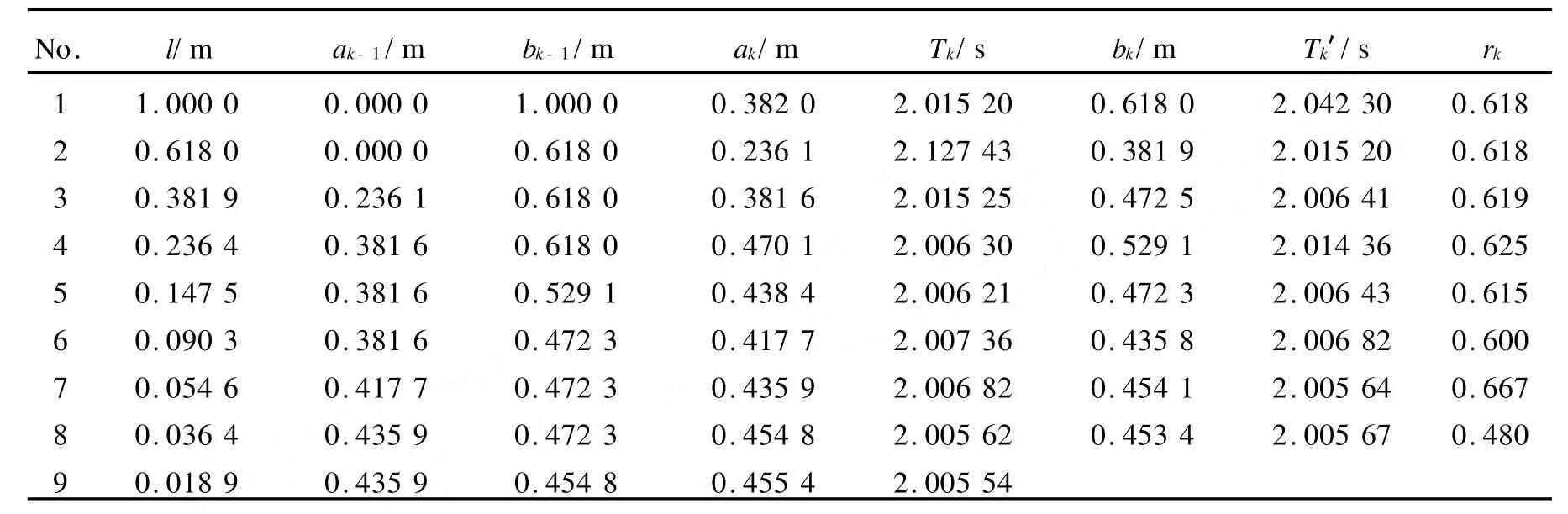
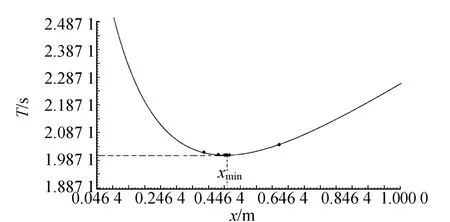
抛物线法又叫三点二次插值法,它是通过已知区间内的三点构造二次函数来逼近已知函数极小值的方法.如果要求将复摆的极小周期Tmin的位置xmin通过实验的方法缩小到l范围内,设L=b0-a0,则取复摆公式的初始区间[a0,b0]内三点x1 下面采用计算机采集实验数据[8],并结合复摆的T-x曲线来研究“0.618”法、Fibonacci法、抛物线法搜索复摆极值点的情况. 取复摆的初始区间[0,1],则区间长度L=1.000 0 m,要求将搜索区间缩小到可以接受的的范围l≤0.020 m,则采用Fibonacci法时,得Fn>50,由Fibonacci数列知n=10,F10=55.表1为用“0.618”法测得的10组实验数据,表2为Fibonacci法测得的9组实验数据,表3为抛物线法测得的4组实验数据. 图3是根据表1,“0.618”法测得数据的9个区间端点在T-x曲线上的位置以及趋近于极值点的情况.图中从左到右第6个点为极值点.此时复摆的极值点位置xmin=0.457 4 m,极小周期T=2.005 57 s. 图4是根据表2,Fibonacci法测得数据的8个区间端点在T-x曲线上的位置以及趋近于极值点的情况.从图中看,从左到右第5个点为极值点,其中第5和第6个点因实验值相近,重叠在一起.此时复摆的极值点位置xmin=0.455 4 m,极小周期Tmin=2.005 54 s. 图5是根据表3实验数据,其中7个数据点在T-x曲线上趋近于复摆极值点的情况,从左至右,第5个点即为实验测得的极值点,与第4个点靠得很近.此时,取Tmin=2.005 53 s,xmin==0.454 5 m. 表1 “0.618”法搜寻复摆极值点的实验数据 表2 Fibonacci法搜寻复摆极值点的实验数据 表3 抛物线法搜寻复摆极值点的实验数据 图3 “0.618”法搜索复摆极值点的情况 图4 Fibonacci法搜索复摆极值点的情况 由以上结果可以看出: 1)以上实验中,按实验要求,“0.618”法用了15次测量(不包括重复数据点),Fibonacci法用了17次测量.由于在“0.618”法的内点中出现了较多的重复数据,使得“0.618”法比Fibonacci法的测量次数较少.由此可见,尽管从理论上讲Fi-犫狅狀犪犮犮犻法比“0.618”法收敛速度快,但是由于受到实验条件的影响,实际情况并非如此. 图5 抛物线法搜寻复摆极值点的情况 2)Fibonacci法搜索复摆极值点比“0.618”法精度高.以上实验中,这2种方法都通过第8组数据比较后,即8次搜索后,Fibonacci法将搜索区间长度缩小到0.018 9 m,而“0.618”法将搜索区间长度缩小到0.021 3 m.因此,采用实验的方法搜寻复摆的极值点,从搜索精度来看,Fibonacci法比“0.618”法较高,但从搜寻速度上看Fibonacci法并非占优势. 3)抛物线法搜寻复摆极值点比“0.618”法和Fibonacci法速度较快且精度较高.从以上实验数据可以看出,抛物线法经过7次测量和4组数据的比较就可以将最小周期点位置缩小到l=0.015 5 m范围内. “0.618”法、Fibonacci法和抛物线法都属于最优化方法中的一维精确搜索法,在实验中将这些方法应用于物理学中复摆的极值点搜寻,抛物线法较“0.618”法和Fibonacci法效果好,测量次数少,而且精度较高;使用Fibonacci法较“0.618”法在搜寻精度上有较好的提高,但是在搜寻速度上并不占优势.不仅如此,还可以用这些方法搜寻物理学中其他单值单峰的极值点问题,在具体应用这些方法时适当地应用它们的优点,有利于得到需要的实验结果. [1] 肖苏,任红.实验物理教程[M].合肥:中国科技大学出版社,2000:149-153. [2] 毛瑞全,刘翠红,郑卿.复摆方程的一种求解方法[J].物理实验,2008,28(3):45-46. [3] 佘守宪,胡颉.黄金数与Fibonacci数列[J].物理与工程,2006,16(2):6-8. [4] Fink D,John H.Mathews and Kurtis.数值方法[M].周璐,陈渝,钱方,译.北京:电子工业出版社,2005:319-321. [5] 袁亚湘,孙文瑜.最优化原理与方法[M].北京:科学出版社,2001:84-89. [6] 薛毅.最优化原理与方法[M].北京:北京工业大学出版社,2004:153-155. [7] 解可新,韩立兴,林友联.最优化方法[M].天津:天津大学出版社,2002:22-24. [8] 梅忠义,倪菱湖,刘向远.黄金分割法在物理实验中的应用[J].大学物理实验,2006,19(2):51-52.3 搜寻复摆周期极值点




4 结束语

