常见的错误矢量式及其分析纠正

刘自华

(湖南化工职业技术学院 湖南 株洲 412004)

矢量是既有大小，又有方向的物理量.由于对矢量概念不太明确，或矢量观念不够强，在一些物理教材或教学参考资料中，在个别教师课堂教学的板书中，在部分学生的作业中，常见到一些形式上的“等式”而实际上并不相等的违反矢量规则的错误矢量式.为了有效地防止对矢量式认识的偏差和错误矢量关系式的漫延，在教学时，教师应当注重明确矢量概念，强化矢量观念，及时纠正错误的矢量式，并注意向学生予以特别的“警示” ，突出教学重点，突破教学难点，提高教学质量.

1 常见的错误矢量式

在一些物理教材中，通常的规定是用黑体字母表示矢量.例如用F表示力矢量，它既包括力的大小，又包括力的方向，而F只表示力的大小，并不包涵力的方向，其合成与分解的运算法则是平行四边形法则.如果在矢量等式中将F写成F，那是错误的.下面列举常见矢量式书写错误的事例.

1.1 将矢量等式错写成数量等式

某杂志关于如图1有这样一个等式

T+N+G=0

(1)

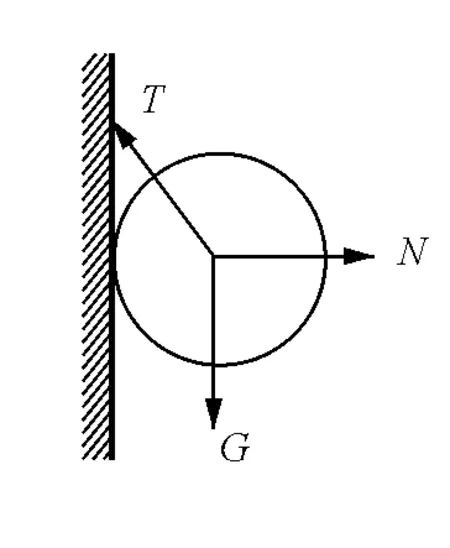
图1 悬挂在墙面小球的受力图

点评：图1中的T、N、G分别表示三个力的大小，T、N、G三个力的方向如图1所示.(1)式中的T+N+G三个量之和只能是表示其数值和关系，并不包括方向关系，三个量的数量和并不等于零，因此(1)式是不成立的.

1.2 一边是矢量错等于另一边的数量

某教材中有如下一个等式[1]

(2)

笔者在某学校听一位名师讲一堂观摩课时，主讲教师在课堂板书时写出如下等式

(3)

1.3 应用公式时出错

某教材中有如下一个等式[2]

(4)

点评：磁场环路定理的表达式为

其等式两边的结果均为数量.(4)式是具体应用磁场环路定理，但(4)式左边的表示为数量，而右边的表示为矢量，这是磁场环路定理应用时出错.

至于在学生作业中，书写的错误矢量式那就五花八门了.常见的错误是将矢量运算与标量运算混为一谈，或求解某矢量时，只求大小而不求方向.所以矢量问题是教学中的难点问题.教师教学时要特别注重突破难点，提高教学质量.

2 原因分析

在比较广泛的面上出现错误矢量式的现象，究其原因，笔者认为主要有以下几个方面.

2.1 思维定势的影响

在其他课程的学习中，或在平时的工作和生活中，或在物理教材不含矢量章节的学习中，与之相联系的大多是数量关系.因此，人们习惯于代数式的书写和运算；书写矢量式既不自然，也不自觉，所以常常不假思考地将矢量式错写成代数式，这是思维定势的影响.

2.2 认识不足的影响

作者或编辑对符号的黑体字母表示矢量，如F、v，白体字母表示标量，如F、v等编排方式认识不足，重视不够，校对也欠细致.个别教师在课堂矢量式的板书规范化方面不严谨*，只注意数值的运算，忽视了一些物理量的方向性.有时也属粗心大意，偶尔出错.

2.3 概念错误的影响

矢量与标量的乘积，矢量与矢量的点乘，矢量与矢量的叉乘等都有严格的运算规则.如3F，F·F，F×F等的含义是完全不同的，如果概念或规律掌握得不够，这个物理教学中的难点就无法突破，(4)式的错误是非常典型的矢量运算概念错误，导致定理应用时出错.

2.4 知识层次的影响

由于矢量知识掌握得不够，考虑问题单一片面，注意了数值，就丢了方向.特别是既要解决数值关系问题，又要解决方向关系问题，对于初接触矢量运算的学生来说，就会感到迷惘，不知所措，这是由于知识层次不高的影响.

3 纠正方法

为了较好地突破这个教学难点，除了教材编者、出版社和教师等都要明确矢量概念，强化矢量式观念，不出差错之外，我们还应从以下几个方面努力.

3.1 明确矢量概念

对于一些物理量中的矢量，在教学时应该特别强调方向，尤其是要引导学生明确其方向的物理意义.例如：重力加速度g，它的方向是竖直向下的.我们对斜抛运动进行分解：在竖直方向是一个匀变速直线运动(向上的匀速直线运动和向下的自由落体运动的合成)，水平方向是一个匀速直线运动，这说明在竖直方向的加速度就负责速度在竖直方向的改变，这就是矢量方向作用的结果.又如一辆汽车以速度v向西运动或向东运动，其结果是完全不一样的，这也是矢量方向作用的结果.特别是解力学、电学、磁学等相结合的题，如果将物理量的方向搞错，那是无法解题的.

3.2 强化矢量观念

在长期的生活和其他课程的学习中，人们建立的标量或代数运算是根深蒂固的.为了加强学生对矢量的认识，出一些思考题来培养学生的矢量观念，如一个力是2 N，另一个力也是2 N，这两个力的合力是多大？如果学生没有树立起矢量观念的话，答案很可能是“0”. 这时教师要进行引导：力是矢量，这两个力夹角的大小可能在0到180℃之间.这时部分学生会给出“0～4 N”范围内的正确答案.这就破除了思维定势的影响，使学生懂得在分析与计算矢量时既要考虑大小，又要考虑方向.

3.3 优化图示作用

对于矢量可以用一根带有箭头的有向线段来表示，矢量的加、减、乘、除运算可以用矢量图示来表示.如图2表示矢量的加减运算.

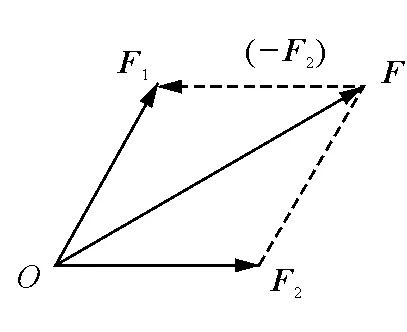
图2 力的平行四边形法则

矢量相加(合成)

F=F1+F2

矢量相减(分解)

F1=F-F2=F+(-F2)

矢量相加(合成)与矢量相减(分解)是互为逆运算的.至于F、F1、F2各自的大小和方向如何，那就要根据平面几何的求解方法分别求出各有向线段的长及指向，亦即各矢量的大小和方向.

3.4 旗帜鲜明地纠正错误

无论教材、资料、学生作业，还是考试中出现的矢量错误，我们都要旗帜鲜明地加以纠正，使学生知道不按矢量规则写就错了，错了就要改.

(1)式的正确表达式

T+N+G=0

教师在教学中的板书式为

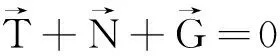
并要强调这两种书写方式的内在联系是等效的.

(2)式正确的表达式为

式中i是单位矢量.

或只考虑电场大小的标量式为

其方向另加说明.

(3)式正确的表达式为

或只考虑大小的标量式为

其方向另加说明.

(4)式的正确表达式为

综上所述，教材编者、论文作者、出版社和教师等物理教学工作者，都要齐心协力堵住出错源头.教师在进行物理教学时，更要特别注意引导学生打破思维定势的影响，明确矢量概念，强化矢量观念，优化图示作用，注重矢量书写规则，正确地书写矢量表达式，有效地突出教学重点，突破教学难点，切实提高教学质量.

参考文献

1 刘克哲.物理学下册.北京：高等教育出版社，1992.11

2 刘克哲.物理学下册.北京：高等教育出版社，1992.100