两等量同号点电荷中垂线上场强的极大点

杨雄生

(北京教育学院朝阳分院 北京 100026)

两等量点电荷连线的中点的场强为零，中垂线上无限远处的场强也为零，中垂线上其他点的场强不为零且是连续变化的，所以，中垂线上有个场强最大值的点．

这个场强最大值的点在那里？

在讨论库仑场的场强问题时，常常会碰到上述问题.如果我们能明确知道这个场强最大值的位置，那么，对讨论问题有很大的帮助．本文就讨论这个问题．

如图1所示，为方便讨论，假定两点电荷的距离为2L．

图1

大家知道，A、B两点电荷在其中垂线上某点P的合场强为

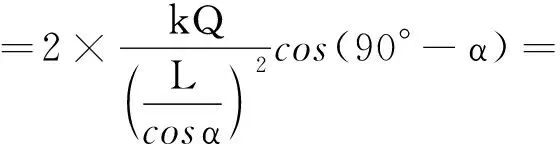
(1)

积化和差，上式可转化为

(2)

上两式中，Q为点电荷所带的电荷量，k为静电力常量，α为点电荷到P点的连线与两点电荷连线的夹角．

由于对称性，本例上下应有两个最大值的位置，我们只讨论连线上方的．根据题意(1)与(2)式自变量α的取值范围为0°至90°．

为求极值点，先对(2)式其求导数为

(3)

上式导数为零的α，可能为极值的位置.我们采用无限逼近的方法来确定最大值的位置．即

3cos3α+cosα=0

(4)

分析上式可知，只有3α超过90°，才可能为零．先试α=40°，发现3cos3α值远远大于cosα，说明α角度大多了，应减小；再选α=35°，发现3cos3α值小于cosα，说明α角小了；但两者相差不多，所以选α=36°，发现3cos3α大于cosα，说明α角大了；再选α=35.5°.同样的推断，由α=35.5°进而α=35.25°；再进而α=35.27°；再进而α=35.26°；最后α=35.265°，这时3cos3α比cosα大0.000 098 399，合场强最大．上述的推理计算过程反映在表1中．

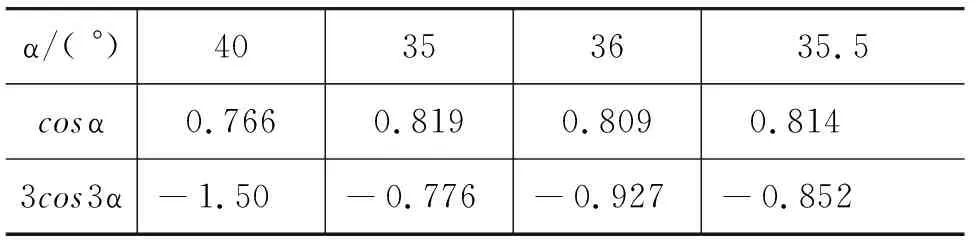
表1

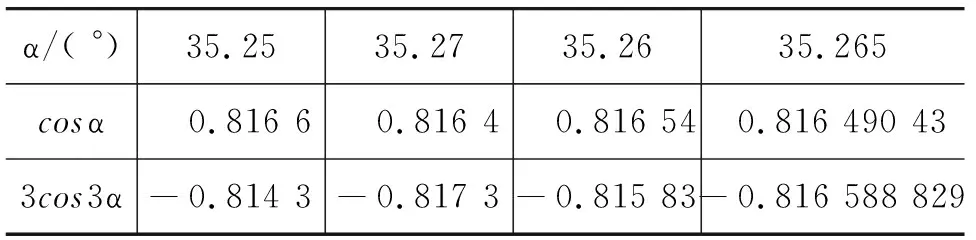
α/( °)35.2535.2735.2635.265cosα0.816 60.816 40.816 540.816 490 433cos3α-0.814 3-0.817 3-0.815 83-0.816 588 829

本例也可以不用求导，直接由(1)式或(2)式用无限逼近法求得最大场强处．只是逼近的次数较多，不如上述方法简便，其逼近过程略．