一类随机服务系统的非参数统计分析与预测

陈 静,杨巧君,周灿灿,梅雪峰

(浙江教育学院理工学院,浙江杭州310012)

1 引 言

研究随机服务系统的主要目的是研究排队系统的效率,估计服务质量,优化排队系统.其求解方法分理论分析和计算机模拟两大类.由于理论分析的复杂性,只有当输入过程和服务时间的分布为某些特殊分布,如指数分布时,随机服务问题的求解才采用理论分析的方法,实际中经常出现非指数分布的输入过程或服务时间,此时应采用计算机模拟求解[1].因此,在实际应用中,求解排队系统的首要问题是如何正确识别输入过程和服务时间的分布,即对实际采集到的数据进行非参数统计推断,这一点被诸多研究者所忽视,如文献[2—5]的研究中均没有对实际数据进行统计分析,而直接假设输入过程和服务时间服从某种分布,然后采用理论分析或计算机模拟方法求解.这种现象的产生可能与经典文献[1]没有作详细说明有关,也可能与研究者不熟悉有关理论有关,因为非参数统计分析[6]与随机服务系统理论分属两大学科.

文献[7]中提出了一类典型的多通道随机服务问题的求解.某医院眼科门诊每天开放,住院部共有病床79张,手术主要分为:白内障、视网膜疾病、青光眼和外伤(急诊).该住院部对非急症病人按照FCFS(First come,First serve)规则安排住院.现需要解决该住院部的病床合理安排问题,并根据当时住院病人及等待住院病人的统计情况,在非急诊病人门诊时即告知其大致入住时间区间.

本文对以上两个问题进行了研究.首先给出了随机服务问题中输入过程和服务时间分布的非参数假设检验和分布函数估计的数学模型,并给出了求解方法;然后对该医院的历史数据进行了相应的统计分析,得出了描述该系统的排队类型及有关指标,并利用分布函数的估计给出了非急诊病人等待时间的预测区间.

2 非参数统计分析模型

令(X,A,P)是一个统计空间,其中P={Pθ:θ∈Θ}为离散型或连续型分布,Θ为k维参数空间,x1,x2,…,xn是取自统计空间的容量为n的样本.

首先考虑分布函数F(x;θ1,…,θk)的估计.

将x1,x2,…,xn按由小到大的顺序排列得次序统计量x(1),x(2),…,x(n),其经验分布函数为

定理1[8,9]对固定的x,(x)依概率收敛于F(x),即对任意给定的ε＞0,

且Dn以概率1收敛于0,即

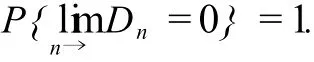
由定理1,经验分布函数是总体分布函数的一个相合估计量.由经验分布分布函数可以估计随机变量在任一区间内取值的概率

即为顾客等待服务的区间估计的计算公式.

其次,考虑非参数假设检验问题

将观测值x1,x2,…,xn分成m个互不相容的小区间(a0,a1],(a1,a2],…,(am-1,am],以ni记子样的观测值落入第i个小区间的频数,i=1,2,…,m.

当k个参数θ1,θ2,…,θk已知时,设

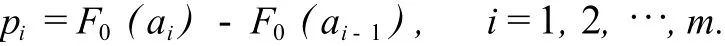
构造统计量

当k个参数θ1,θ2,…,θk未知时(设m＞k+1),记它们的极大似然估计为

构造统计量

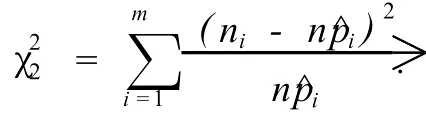
定理2[8,9]设F0(x;θ1,θ2,…,θk)为总体的真实分布,即H0为真,当n→时,有

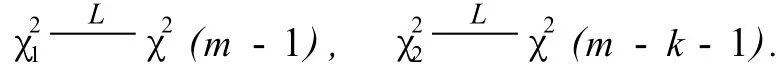
定理3[8,9]设F0(x;θ1,…,θk)为连续型总体的真实分布,即H0为真,有

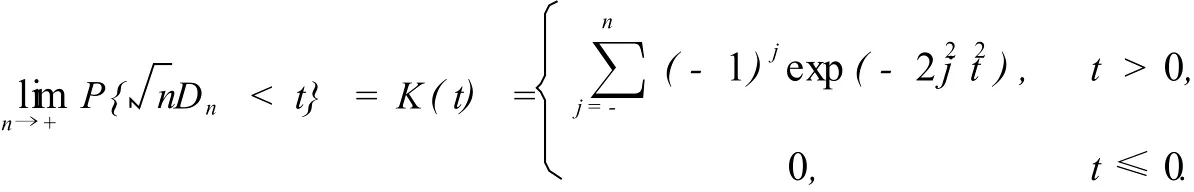
依据定理2的假设检验称为Pearsonχ2检验,依据定理3的检验称为Kolmogorov-Smirnov检验.前者虽然对离散型和连续型分布都适合,但通常在离散型分布时使用,后者对连续型分布更适合.

在实际中,通常给出大量的观测数据,利用以上的理论采用手工计算极其复杂,一般宜采用相关的数学软件计算.Matlab软件由于其强大的功能、众多的内置函数、直观的图形显示和丰富的工具箱,可以很方便的完成分布函数估计和非参数假设检验[10].

3 医院眼科排队问题的数据分析与预测

对文献[7]中的排队问题,其输入过程为每天到达的各类病人数,服务时间即为病人从看门诊到出院的总时间,可分别视为离散型分布和连续型分布,故首先采用Pearsonχ2检验和Kolmogorov-Smirnov检验,判断他们各自的分布情况.

排队系统中,通常认为到达顾客数服从Poisson分布,采用Matlab计算,输入过程的有关检验及统计结果见表1,各类病人到达比例见图1,每天排列队长见图2,其直方图和理论结果对照图见图3.

表1 每天各类病人到达数的非参数假设检验(显著性水平0.05)

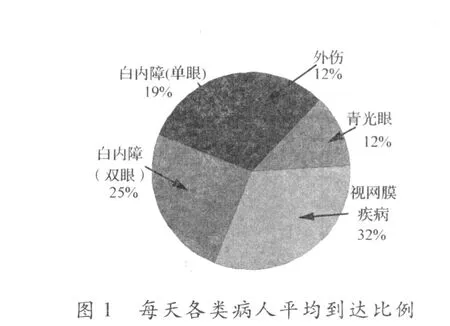
由结果可知,在显著性水平0.05,接受原假设,可认为各类病人到达数均服从Poisson分布.每天平均到达病人数8.7人;到达的病人中视网膜疾病患者最多,大约占32%,其次是白内障(双眼)、白内障(单眼)患者,分别占25%和19%,青光眼和外伤患者最少且大致相等,均占12%.由图2可知,该医院眼科门诊服务系统的排队长在10天左右即进入稳态,稳态后排队长的平均值为96人.

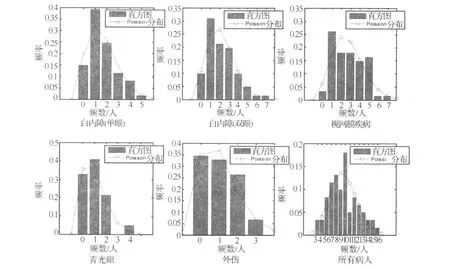
图3 每天各类病人到达数直方图及理论Poisson分布曲线

各类病人的服务时间的直方图见图4.采用Kolmogorov-Smirnov检验,在显著性水平0.05下,他们均不服从通常排队系统中的负指数分布,也不服从正态分布、均匀分布等常见连续型分布.因此,可以知道该医院眼科排队系统属于M/G/C//系统.

图4 各类病人服务时间的直方图

确定排队系统的类型后,预测非急诊病人门诊后的等待时间的通常方法是采用计算机模拟方法,利用上小节给出的分布函数的估计方法,我们可以得到更加方便和简单的估计方法.

设各类非急诊病人等待住院时间的理论分布函数为F(x),依据定理1,我们用经验分布函数(x)作为总体分布的近似,然后采用公式(1)计算等待住院时间在以均值为中心的区间的概率,给定置信水平1-α后,找出大于等于95%的区间,即为所求的预测区间.

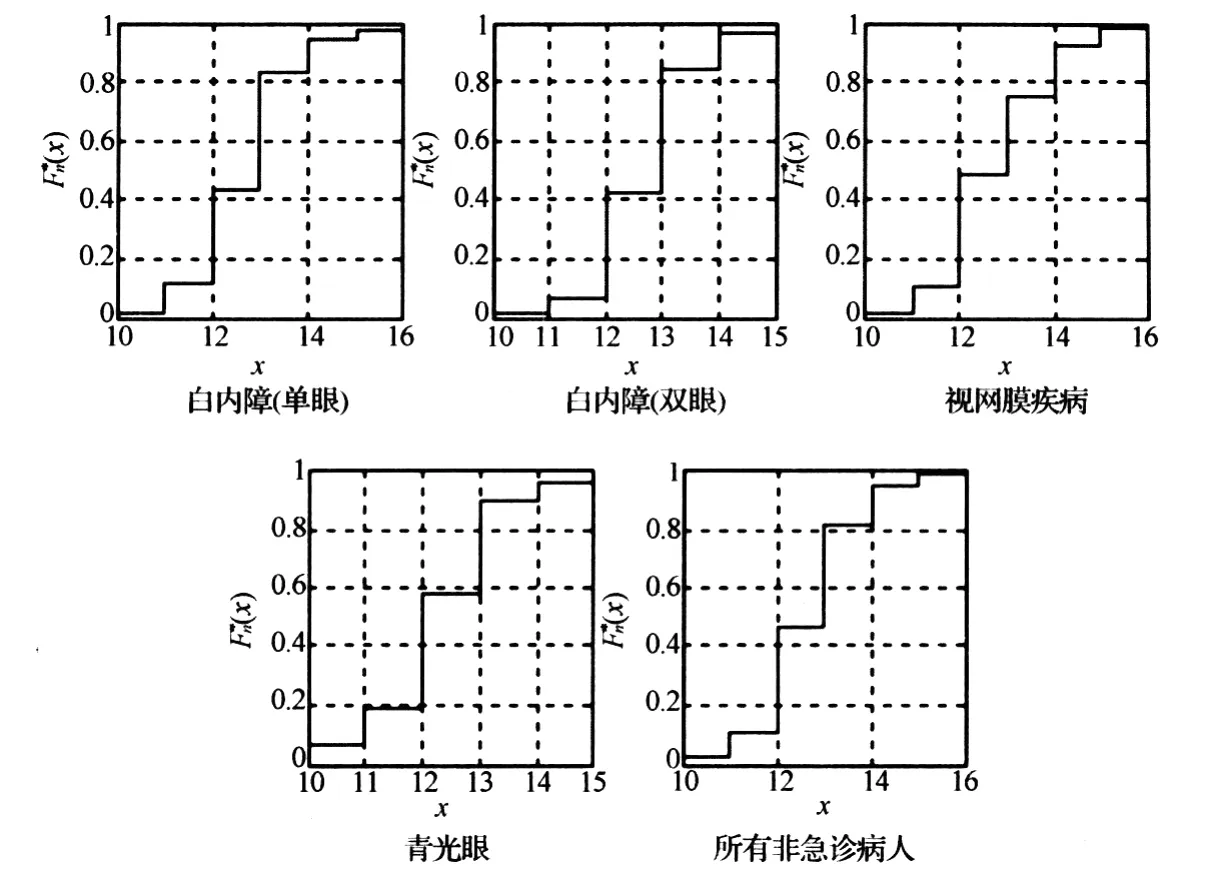
图5 各类非急诊病人等待住院时间的经验分布函数

计算出各类非急诊病人等待住院时间的经验分布函数,曲线图见图5,相关统计指标见表2.

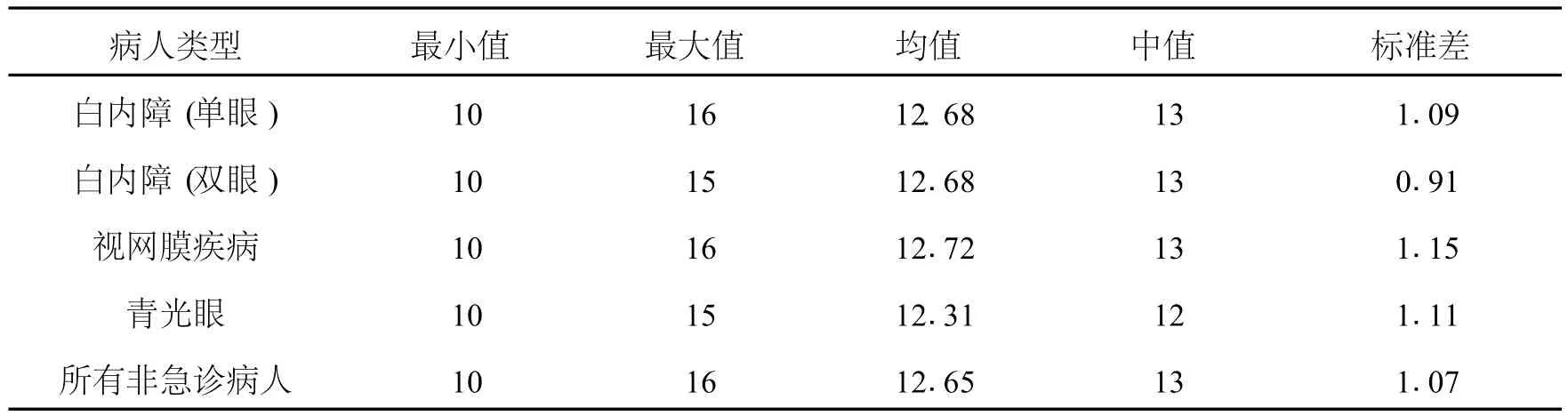
表2 各类非急诊病人服务时间有关统计指标

所有非急诊病人等待时间的经验分布函数为

可以计算得到非急诊病人等待入住时间的区间及概率如表3.

表3 各类非急诊病人等待入住时间区间的概率

故取置信度0.90时,非急诊病人等待入住时间的预测区间为[11,14];取置信度0.85时,非急诊病人等待入住时间的预测区间为[12,14].

4 结 论

本文以非参数统计分析理论为指导,给出了随机服务系统中输入过程及服务时间的非参数假设检验,以及分布函数估计的数学模型,并基于经验分布函数导出了顾客等待服务的区间估计的计算公式.然后对文献[7]中的历史数据进行了统计分析,得到了该医院眼科排队系统的类型,给出了病人等待住院的预测区间.

4.1 在对随机服务系统进行求解之前,必须利用历史观测数据采用非参数假设检验,判断出服务系统的类型.根据输入过程和服务时间为离散型分布或连续型分布的情形,分别采用Pearsonχ2检验或Kolmogorov-Smirnov检验.

4.2 基于经验分布函数导出了顾客等待服务的区间估计的计算公式(1),避免了求解此类模型通常采用的较复杂的随机模拟法.

4.3 对历史观测数据做非参数假设检验,在0.95的置信水平下,文献[7]中的FCFS随机服务系统属于M/G/C//系统;取置信度0.90时,非急诊病人等待入住时间的预测区间为[11,14];取置信度0.85时,预测区间为[12,14].

本文是在“2009年全国大学生数学建模竞赛”参赛文章(获浙江省二等奖)的基础上,通过参考命题者提供的解答要点,进行修改整理而得.

[1]《运筹学》教材编写组.运筹学[M].北京:清华大学出版社,1990.

[2]李红,严建渊.一个随机服务系统的计算机模拟[J].数学的实践与认识,2006,36(8):239-242.

[3]麦宇雄,卢永昌,覃杰.随机服务系统(排队论)在集装箱码头大门设计中的应用[J].水运工程,2007(5):39-42.

[4]王启栋,张康莉,刘召平,等.医院科室病床使用情况的综合评价分析[J].中国医院统计,2001,8(2):103-105.

[5]宋萍.用TOPSIS法对医院床位利用情况进行综合评价[J].重庆医学,2003,32(4):455-458.

[6]陈希孺,柴根象.非参数统计教程[M].上海:华东师范大学出版社,1993.

[7]全国大学生数学建模竞赛组委会.2009高教社杯全国大学生数学建模竞赛A题[EB/OL].[2009-10-10].http://mcm.edu.cn/mcm09/Problems2009c.asp.

[8]魏宗舒.概率论与数理统计教程[M].2版.北京:高等教育出版社,2008.

[9]史宁中.统计检验的理论与方法[M].北京:科学出版社,2008.

[10]薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].2版.北京:清华大学出版社,2008.