基于排队论的眼科病床合理安排的数学模型

汪 琴,岑璐局,张渊娴,马新生

(浙江教育学院理工学院,浙江杭州310012)

1 引 言

对医院病床进行合理安排,有效减少病人的排队等待时间,提高医疗资源的使用效率,具有重要的理论和实际意义.文献[1]中提出了某医院眼科病床合理安排的评价和优化问题.该眼科门诊每天开放,住院部共有病床79张.眼科手术主要分四大类:白内障、视网膜疾病、青光眼和外伤.外伤疾病属于急症,住院后第二天便安排手术,其他病人采用FCFS(First come,First serve)规则安排住院.医院提供了50天349名已出院病人、79名住院病人及102名等待住院病人情况的历史数据记录.问题一,建立合理的评价指标体系,用以评价病床安排模型的优劣.问题二,试就该住院部当前的情况,建立合理的病床安排模型,并对该模型利用问题一中的指标体系作出评价.问题三,根据当时住院病人及等待住院病人的统计情况,在病人门诊时即告知其大致入住时间区间.问题四,若该住院部周六、周日不安排手术,医院的手术时间安排是否应作出相应调整?问题五,在一般情形下,医院病床安排可采取使各类病人占用病床的比例大致固定的方案,就此方案建立使得所有病人在系统内的平均逗留时间(含等待入院及住院时间)最短的病床比例分配模型.

该问题属于多通道随机服务问题.文献[2,3]分别采用秩和比法和TOPSIS法讨论了医院病床使用效率的评价方法,文献[4]讨论了一类简单的M/M/1医院排队系统的优化问题.这些方法和已有的排队论理论[5]均无法直接解决以上问题.

本文以排队论理论为指导,引入病人满意度和病床利用率两个评价指标,在对大量历史数据进行详细统计分析的基础上,建立了眼科病床合理安排的数学模型,给出了以上问题的解决方案.

2 模型假设及数据的初步分析

综合理论和历史数据分析的需要,本文作如下假设:

(1)病人数据源是无限的;

(2)不同病人的入院时间与住院时间均为独立同分布随机变量序列,且与病人的年龄、性别等因素无关;

(3)考虑理想化的病人排队系统,忽略其他可能改变病人等待住院、手术及出院时间的因素,也不考虑病人发生死亡或手术医疗事故等意外情况;

(4)由于医院条件的限制,白内障手术只能安排在每周一、周三做.

排队论理论是通过对服务对象到来及服务时间的统计研究,得出这些数量指标(等待时间、排队长度、忙期长短等)的统计规律,然后根据这些规律来改进服务系统的结构或重新组织被服务对象,使得服务系统既能满足服务对象的需要,又能使机构的费用最经济或某些指标最优[5].在进行分析之前,必须首先识别每天到达病人数和病人住院时间的统计分布规律.为此,采用Pearsonχ2检验[6],并利用Matlab软件计算得到,在显著性水平α=0.05时,每天到达病人数服从参数λ=8.69的Poisson分布(此时p=0.5586),病人住院时间不服从负指数分布(此时p=0.0000),直方图分别如图1、图2所示.因此,本医院排队系统属于M/G/C/∞/∞系统.

图1 每天到达病人数直方图

图2 病人住院时间直方图

3 模型的建立与求解

3.1 评价指标体系模型及“问题一”的求解

要评价医院现有的病床安排模型——FCFS的优劣,就需要我们确定合理的评价指标体系.兼顾等待住院病人队列的长度和医院资源的利用率这两个因素,我们定义病人满意度和医院病床利用率两个评价指标,用以评价病床安排模型的优劣.

定义1 病人满意度

记i表示按时间先后顺序对病人的编号,每个病人从住院到第一次手术之间的间隔时间为ti,i=1,2,…,349,它们的平均间隔时间为,则每个病人的满意度为

平均满意度为

定义2 医院病床利用率

记n表示对日期顺序的编号,n=1,2,…,50.每天的出院人数为cn,则每天医院病床的有效利用率为

病床的平均有效利用率为

图3 每个病人的满意度

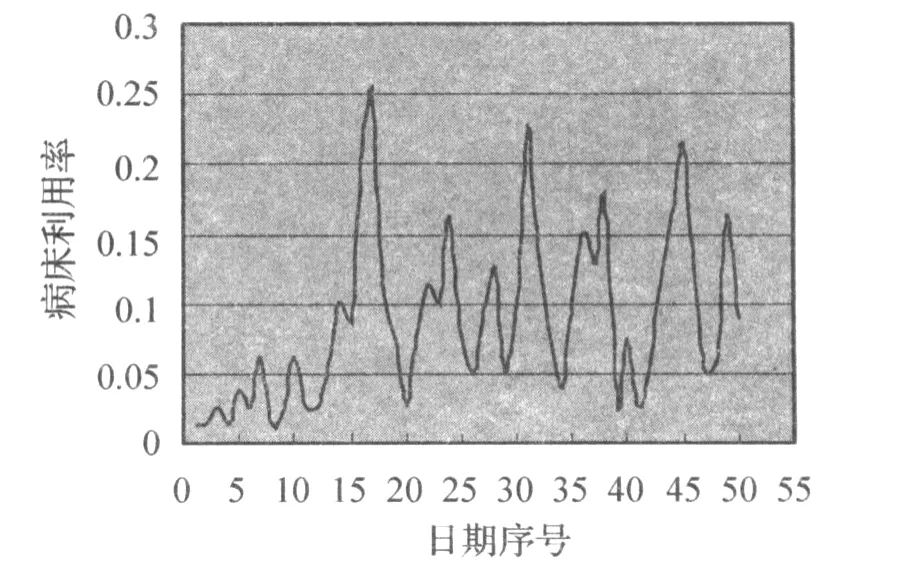
图4 每张病床的有效利用率

从病人的满意度看,由于采取了外伤病人优先安排住院原则,即外伤病人在门诊后的第二天便可以住院,所以外伤病人的满意度达到最大值,都为1,但是相比之下,其他病人的满意度不恒定,这就导致了不同病人之间的满意度存在很大差距,使得满意度具有明显的波动性.这说明该病床安排模型不能很好满足所有病人的要求.

从病床的有效利用率看,病床的有效利用率不高,且每天的起伏很大,不能做到每天都使病床得到最充分的利用,从而说明该病床安排模型不是非常合理.

因此,当前该医院住院部对全体非急症病人运用的FCFS先到先服务的规则安排住院,虽然操作简单,也满足了急症病人的需求,但效率不高,没有考虑等待住院病人队列的长度,即病人的等候时间,也没有使医院的资源,即住院部所提供的病床得以充分的利用.

综上所述,采用FCFS规则不适合解决安排住院的问题.

3.2 M/G/C/／排队系统模型及“≤问题二”的求解

由于病人每个病人住院必需排队等待,故本系统具有多个通道,且每队队长没有限制.又医院眼科共有病床79张,故具有多个服务台,且各服务台工作是相互独立的,平均服务率相同,即μ1=μ2=…=μc=μ,其中c=79.因此,本问题的排队属于M/G/C//系统.整个服务机构的平均服务率为cμ,其中c=79,令＜1时才不会排成无限的队列,称ρ为这个系统的服务强度或称服务机构的平均利用率(见图5).

图5 系统的服务强度

在分析这排队系统时,仍从状态间的转移关系开始,如状态1转移到状态0,即系统中有一名病人被服务完了(出院)的转移率为μP1;状态2转移到状态1时,即在两个服务台上被服务的病人中有一个被服务完成而出院,因为不限是哪一个服务台,所以这时的转移率便是2μP2.同理,再考虑状态n转移到n-1的情况.当n≤c时,状态转移率为nμPn,当n＞c时,因为只有c个服务台,最多有c个病人在被服务,n-c个病人在等候,因此这时的状态转移率应为cμPn.

故我们可以得到

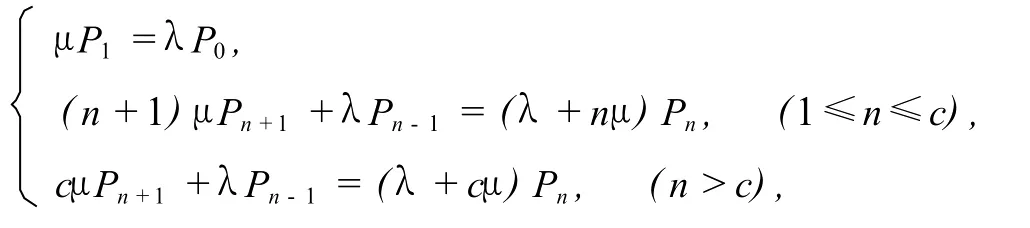
用递推法解上述差分方程,可求得状态概率.

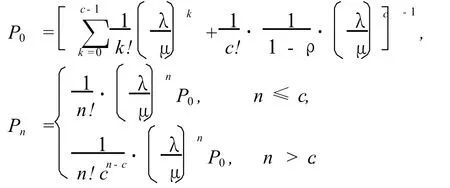
系统的运行指标平均队长、平均等待时间和逗留时间分别为

为达到排队系统的最优化,我们认为考虑该问题的出发点有以下几点:①最大限度地满足病人的基本住院需求,平时尽可能使病床负荷率保持在一定水平,从而减小对急需住院治疗的拒收率;②尽可能提高病床的利用率,以充分利用医院现有的资源;③尽量减少一般病人住院等待时间,缩短等待住院病人t队列的队长.

显而易见,以上三项要求之间存在着矛盾,不能只为了满足其中一项要求而牺牲另一项甚至两项要求,因此,如何协调上述三项要求,寻求总体综合效益优化便是本题的中心.

由于白内障手术只在周一和周三做,且做双眼是周一先做一只,周三再做一只,并且周一和周三只安排白内障手术,其他眼科疾病(除急症外)都不安排在周一、周三.所以若根据FCFS规则安排住院,便会导致一些病人在住院后不能及时被安排手术,最多的病人住院后等待了6天才被安排手术.为此我们对FCFS的病床安排模型进行改进.

图6 M/G/C/∞/∞

对在周一、周三至周六住院的白内障病人筛选出来,把他们都安排在周二、周日住院,这样就能保证白内障病人在住院后的第二天就能接受手术,提高了医院病床的利用率.对在周一至周六住院白内障(双眼)病人都安排在周日住院.不仅如此,我们还根据青光眼和视网膜疾病的手术不安排在周一和周三进行,所以我们筛选出在周六和周一住院的青光眼和视网膜疾病的病人,把他们的住院时间推迟一天,即周日和周二住院,这样便保证了这些病人在医院里准备2天后都能够及时地进行手术.由于我们对一些病人的住院时间进行了调整,使得医院有了更多的空床位,尤其是对白内障(双眼)病人住院的时间推迟得比较久,部分病人推迟了6天左右,我们便筛选出在他们之后住院且住院时间小于6天的病人,对他们的住院时间提前,这样做不仅缩短了病人的等待住院时间,使等待住院病人队列缩短,还提高了医院资源的有效利用率.图6是我们解决该问题的思路与方案.

根据以上的分析,利用MATLAB进行编程,在原有的FCFS病床安排模型的基础上进行修改,设计病人住院安排如表1.

表1 病人住院安排表

3.3 区间估计模型及“问题三”的求解

为了能够让病人在门诊时就能被告知大致入住医院的时间区间,我们根据当时已经出院病人的数据,统计得到除急症病人外,其他病人的平均住院时间,然后建立区间估计模型[6],对门诊病人的住院时间进行估计.

在不考虑外伤的情况下,可近似认为病人的服务时间即等待时间ξ服从正态分布N(μ,σ2),其中方差σ2未知,故平均等待时间μ的置信度为1-α=0.95的置信区间为[6]计算可得,置信区间为(12.5391,12.7595).

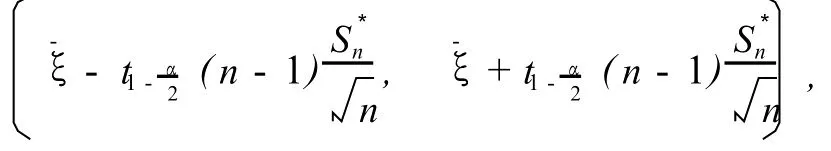
故可以在病人门诊时告知其大致入住院时间区间为(12,13),即住院时间大概是在门诊后的第12或13天.

3.4 “问题四”模型的建立与求解

基于问题二的求解方法,考虑该住院部周六、周日不安排手术的情况,我们对医院的手术时间做相应的调整.由于我们假设白内障手术只在周一和周三进行,故该条件对白内障病人不受影响,只对青光眼和视网膜疾病的部分病人进行调整.再借鉴问题二中建立的M/G/C//排队模型,对新的住院安排表进行相应的调整,便能够做到在周六周日不进行手术的前提下,不仅保证外伤疾病的病人能在门诊的第二天就能住院,且在住院后的下一天进行手术,还保证其他的病人都能够在住院后的1∽2天内接受手术.

沿用“问题二”中的方法,利用MATLAB求解,计算得到了每天病人的住院安排表,如表2所示.这时,病人的满意度为=0.67,病床的平均有效利用率为=0.080,均有所降低.

表2 病人住院安排表

3.5 多指标床位分配模型及“问题五”的求解

为求解问题五,我们改进文献[7]中的多指标席位分配模型,建立多指标床位分配模型.

该问题可描述如下:设共有n种病人,第i种病人的人数为ai(i=1,2,…,n),记a=影响床位分配的因素有l个,第j个因素对第i种病人影响的指标值为xij(i=1,2,…,n;j=1,2,…,l),指标矩阵为

通常指标值分为“效益指标”“成本指标”和“固定指标”.所谓效益指标是指标值越大越好的指标(病床周转率),成本指标是指标值越小越好的指标(平均逗留时间),固定指标是指标值稳定在某个固定值为最好的指标(病床利用率).

考虑到不同指标属性不同,量纲也可能不同,作如下规范化处理:

对于效益指标,令

对于成本指标,令

对于固定指标,令

其中xij＊为第j个影响因素对第i种病人的最佳指标值.

利用公式(2)∽(4)将指标矩阵(1)化为规范指标矩阵

利用主观赋值法或客观赋权法确定权重wi(j=1,2,…,l).

计算各种病人的加权综合指标和整个系统的综合指标

多指标床位的合理分配应该按各种病人综合指标的比例来分配,即尽可能地满足各种病人的“综合配于是我们得到多指标床位合理分配模型如下:

其中,xi为整数,i=1,2,…,n.

该模型求解方法:首先,枚举求出满足约束条件

比较相应目标函数值的大小,最小者即为模型最优解.

在本问题中,我们既要考虑保证医院给病人提供需要的医疗服务,又要考虑医院卫生资源的合理利用及其长远的发展,还要根据题目要求对平均逗留时间的权重进行优先考虑.具体求解如下.

根据历史数据进行统计分析得到各类病人各个指标的数据,给出指标矩阵X,见表3.

表3 指标矩阵X

利用公式(2)∽(4)将指标矩阵X转化为规范化指标矩阵E,见表4.

表4 规范化指标矩阵E

权重wj(j=1,2,…,l)取值见表5.

表5 权重值表

利用公式(6)计算各类型的加权综合指数和系统综合指标,得

建立相应的多指标床位分配模型,转化为等价连续型非线性模型,求出相对合理的病床分配比例,如表6所示.此时,所有病人在系统内的平均逗留时间(含等待入院及住院时间)最短,为13.23天.

表6 病床分配比例

4 结 论

本文针对文献[1]提出的问题,以排队论为理论基础,建立了眼科病床合理安排的数学模型,该模型综合考虑了病人和医院两方面的利益,与实际紧密联系且具有可操作性,采用数学软件进行计算,结果较为准确.

(1)利用假设检验理论,对医院现有历史数据进行了统计分析,得到每天到达病人数服从参数λ=8.69的Poisson分布(此时p=0.5586),病人住院时间不服从指数分布(此时p=0.0000),近似服从正态分布.据此,该医院排队系统属于M/G/C/／系统.

(2)建立了评价指标体系模型.给出了病人满意度和医院病床利用率两个指标,用以评价病床安排的优劣,这是排队论理论在医院病床安排的应用,是对经典排队论评价指标的推广,具有直观、计算简单的特点.计算可得,原有系统的平均满意度y-=0.55,病床的平均有效利用率g-=0.087553.然后,基于M/G/C/／系统,给出了新的排队规则,此时病人的平均满意度y-=0.79,医院病床的平均有效利用率g-=0.088713,两个指标均有显著改善.

(3)建立了病人等待时间的区间估计模型.基于FCFS排队规则,在0.95的置信度下,病人等待时间是12到13天.

(4)在周六周日休息的假设下,重新给出了住院安排方法,此时,病人的平均满意度y-=0.67,病床的平均有效利用率g-=0.080,均有所降低.

(5)建立了以所有病人在系统内的平均逗留时间(含等待入院及住院时间)最短为优化目标的多指标床位分配模型.得到五种病人的床位分配是17,18,9,23,12,平均逗留时间为13～14天.

排队论模型的应用非常广泛,因而适用于现实中的一切服务系统,故本文给出的模型可以推广到其他的服务系统中,例如通信系统、交通系统、计算机、存贮系统、生产管理系统等.

本文是在“2009年全国大学生数学建模竞赛”参赛文章(获全国二等奖)的基础上,通过参考命题者提供的解答要点,进行修改整理而得.

[1]全国大学生数学建模竞赛组委会.2009高教社杯全国大学生数学建模竞赛B题[EB/OL].[2009-10-10].http://mcm.edu.cn/mcm09/Problems2009c.asp.

[2]王启栋,张康莉,刘召平,等.医院科室病床使用情况的综合评价分析[J].中国医院统计,2001,8(2):103-105.

[3]宋萍.用TOPSIS法对医院床位利用情况进行综合评价[J].重庆医学,2003,32(4):455-458.

[4]韩新焕,朱萌纾,吴静.医院管理系统中排队模型的优化决策分析[J].数理医药学杂志,2008,21(1):16-18.

[5]《运筹学》教材编写组.运筹学[M].北京:清华大学出版社,1990.

[6]魏宗舒.概率论与数理统计教程[M].2版.北京:高等教育出版社,2008.

[7]付必胜,杨益民,张华.多指标席位分配模型及其应用[J].数理统计与管理,2009,28(4):660-665.