Matlab辅助机构运动学分析

曾德惠

(湖北民族学院 理学院,湖北 恩施 445000)

机构的运动学分析,就是从几何的角度出发,在已知机构尺寸及原动件运动规律的基础上,求解机构中其余构件的运动参数,包括构件上点的轨迹、位移、速度、加速度以及构件的角位移、角速度和角加速度[1].无论分析评价现有机械的运动性能,还是设计优化新机械,对机构进行运动分析都是十分重要的,同时它还是研究机械动力性能的必要前提.

机构运动分析的方法主要有图解法和解析法两种.图解法是运用理论力学中的速度、加速度合成原理列出机构上相应点之间的相对运动矢量方程，以一定比例尺画出对应的矢量多边形,用几何的方法得出相应的运动参数.解析法的关键是建立位移方程式,速度与加速度分析则是利用位移方程式对时间求导一次、二次而解线性方程的问题.常用的解析法有向量法、复数法[2]、矩阵法等,就其核心都是建立闭环矢量方程[3].

图解法形象直观、易于掌握,适于机构某瞬时运动参数的计算.而解析法借助计算机,可以获得系列结果和运动线图,适于机构整个运动过程的运动分析.本文以工程上广泛应用的平面四杆机构为例,采用解析法中的矩阵法建立数学模型,通过Matab编程实现机构的运动学分析,并给出具体实例来探讨说明运动学的计算机辅助分析及应用.

1 机构运动学分析数学模型的建立

利用计算机对机构进行解析法运动分析时,大致的方法步骤为:机构运动简图-数学模型-Matlab编程调试-输出结果及分析.

将力学模型转换为数学模型是编程计算的关键.机构运动学分析以机构运动简图为基础,应用理论力学原理,充分利用矢量、矩阵、线性方程等数学工具,将力学模型用数学方法简洁地描述出来[4].

图1 平面四杆机构运动简图

运动学分析要预先知道机构的几何特性,即各构件的长度.图1所示为四杆机构的运动简图,已知杆长分别为L1、L2、L3和L4,设曲柄AB绕A点以角速度ω1匀速旋转,要求分析各杆的运动情况,并以连杆BC中点E为例说明杆件上点的速度和加速度的求解.按照以下的方法和步骤建立该四杆机构运动学分析的数学模型.

1.1 位移分析

用解析法作机构运动分析的关键是位置方程的建立和求解.首先,在运动简图的基础上建立直角坐标系,将各构件表示为杆矢量,再根据各杆矢量构成的封闭图形,写出机构的闭环矢量方程式[5-7].

如图1所示,以A点为坐标原点设定机构的Axy坐标系,将x轴设在机架AD连线上,并标出各杆矢量的方位角.约定和假设:由x正向旋转到矢量的矢端若为逆时针转动,则该矢量方位角为正；杆件之间夹角的表示与矢量方位角的表示相一致.

1)构件角位移分析

考虑各杆长度保持不变，四杆机构ABCD闭环矢量方程为:AB+BC-AD-DC=0,即:

L1+L2-L3-L4=0

(1)

由式(1)向x、y轴上分别投影得四杆机构的角位移方程(2):

L1cosθ1+L2cosθ2-L3cosθ3-L4=0

L1sinθ1+L2sinθ2-L3sinθ3=0

(2)

式(2)包含两个非线性方程,解此非线性方程组可求出两个未知的方位角.

2)构件上点的位置分析

构件上各点位置由点的坐标确定.这里以连杆BC上的中点E为例加以说明.E点位置坐标如下：

xE=L1·cosθ1+L2/2·cosθ2

xE=L1·sinθ1+L2/2·sinθ2

(3)

1.2 速度分析

1)构件角速度分析

为求各杆的角速度,将机构的坐标投影方程(2)中各式分别对时间t取一阶导数,再把已知数据放在方程右边,未知角速度放在方程左边,整理写成矩阵形式如式(4),求解即可得出杆BC和CD的角速度ω2和ω3.

(4)

2)构件上点的速度分析

为求点的速度,可将点的位置方程对时间t取一阶导数.对式(3)求导得出连杆BC上中点E的速度方程,写成矩阵形式如下：

(5)

1.3 加速度分析

1)构件角加速度分析

为求各杆的角加速度,可将角速度方程(4)式对时间t求一阶导数,整理写成矩阵形式的角加速度方程如式(6),求解即可得出杆BC和CD的角加速度α2和α3.

(6)

2)构件上点的加速度分析

由式(3)对时间t求二阶导数,或由(5)式对时间t求一阶导数得出连杆BC上中点的加速度方程，写成矩阵形式如下：

(7)

上述方法同样适用于复杂机构以及构件上任意点的运动分析.

2 Matlab编程求解

由前面的分析可见,式(2)的位置方程当θ1已知时是包含两个未知量θ2、θ3的非线性方程组,手工计算难度很大,但运用Matlab的优化工具箱函数fsolve能对它方便地求解.该函数相当于对矢量方程(2)等式左边就目标值 0 寻优求值,求解方法步骤如下[3,8-10]：

2.1 位置方程的Matlab编程

1)建立函数文件Position .m子程序

function F=Position (theta23,theta1,L1,L2,L3,L4)

F=[L1*cos(theta1)+L2*cos(theta23(1))-L3*cos(theta23(2))-L4;

L1*sin(theta1)+L2*sin(theta23(1))-L3*sin(theta23(2))];

2)主程序中在给定的初值下,调用fsolve函数求方程的根

[theta2,theta3]=fsolve(@Position,[pi/6;pi/3], ptimset('display','off'),theta1,L1,L2,L3,L4) ;

其中: Position是求解未知量θ2、θ3的函数名;[pi/6;pi/3]是对待求量的初始猜测值.

2.2 速度、加速度方程的Matlab编程

速度和加速度的计算只需求解线性方程组,如式(4)～(7)用矩阵形式建立起一个数学模型AX=B.根据线性方程组的不同特点,一般可选用直接法和迭代法求解.直接法分为运算符求解和矩阵分解求解,通过对矩阵和Matlab相关函数的操作实现,如除法命令X=AB或B/A,函数lu()等等;迭代法分为Gauss-Seidel迭代法、jacobi迭代法、超松驰迭代法和两步迭代法,需要自编一段程序实现[4].本文采用除法命令X=B/A直接法求解未知速度或加速度.

2.3 程序运行结果及可视化

以L1=20 mm,L2=35 mm,L3=30 mm,L4=40 mm,ω1=4 rad/s,α1=0,杆件转角θ2、θ3寻优初值分别为30°和60°作为具体实例编程,用计算机求解得到各运动参数数值列表如下：

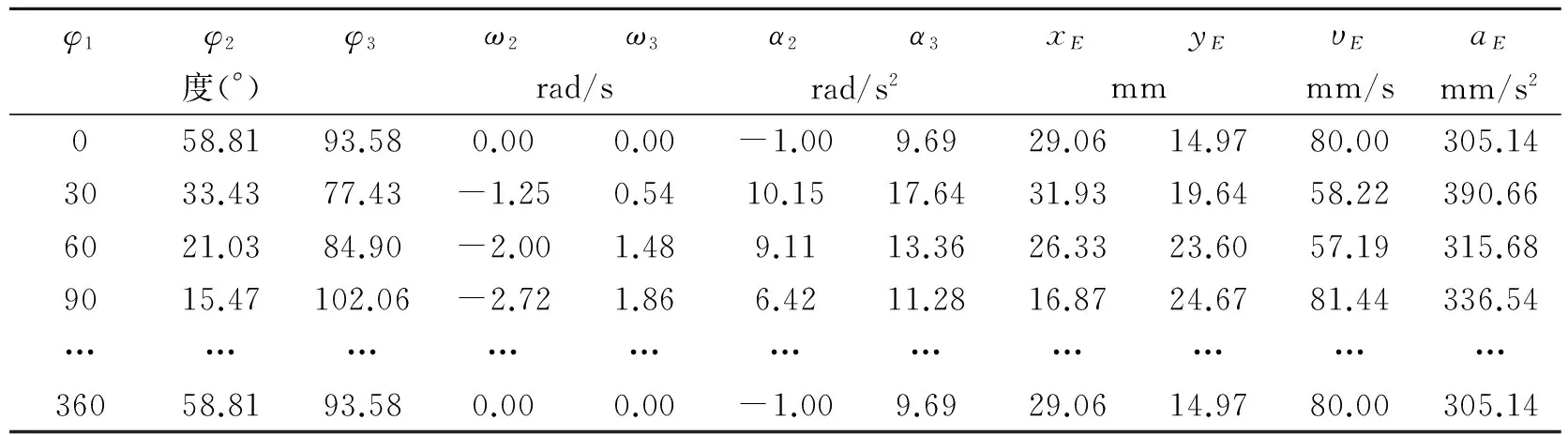
表1 运动参数列表

为了进一步掌握机构的性能,可以根据表1所列数据利用Matlab编程作出机构在一个运动循环中的运动线图,用plot 函数[10]将计算结果可视化如图2～5所示.

图2 BC、CD杆转角曲线

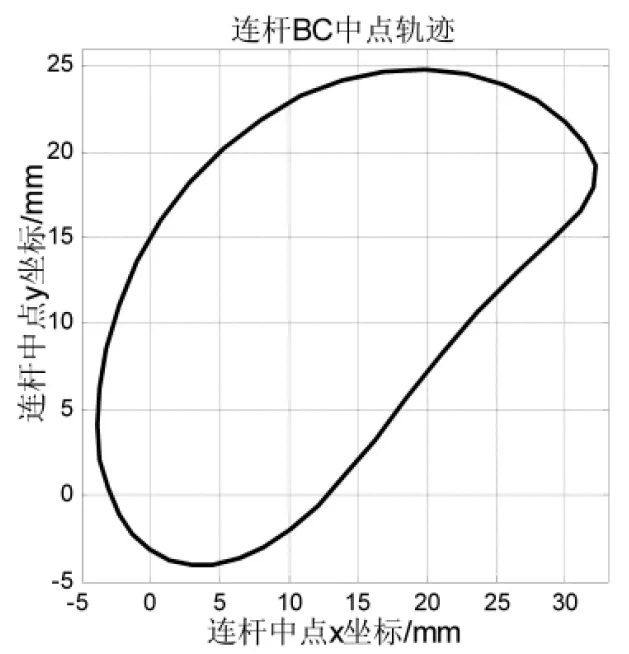
图3 连杆中点轨迹曲线

图4 BC、CD杆角速度曲线

图5 BC、CD杆角加速度曲线

3 结束语

在机构的运动分析中,根据运动简图建立机构的闭环位置矢量方程,再用投影和求导的方法可方便地建立速度及加速度方程,转化为矩阵形式,容易引入Matlab编程计算,借助于计算机辅助手段,把学生和设计人员从繁杂的数学计算和枯燥的编程中解放出来,为解决类似工程技术问题提供了行之有效的方法和手段.

[1] 邹慧君,张春林,李杞仪.机械原理[M].北京:高等教育出版社，2006.

[2] 吉知难,杨悦.复极矢量法在机构运动分析中的应用[J].机械与电子,2008,26(6):67-68.

[3] 约翰·F·加德纳.机构动态仿真:使用MATLAB和Simulink[M].周进雄,张隆，译.西安：西安交通大学出版社,2002.

[4] 曾德惠.Matlab辅助工程静力学分析[J].湖北民族学院学报:自然科学版，2010,28(1):72-75.

[5] Edward B.Magrab.MATLAB原理与工程应用[M].高会生,李新叶,胡智奇,等,译.北京:电子工业出版社,2002.

[6] 郑树琴,成建平,王大江.曲柄摇杆机构运动轨迹计算机仿真[J].太原理工大学学报,2001,32(3):290-292.

[7] 王永超.基于Matlab的机构运动仿真方法及其比较[J].计算机仿真,2004,21(8):82-84.

[8] 苏金明,阮沈勇,王永利.Matlab工程数学[M].北京:电子工业出版社,2005.

[9] 胡晓珍,陈忠维.基于MATLAB/fsolve函数的四连杆机构运动轨迹仿真[J].机械工程师,2007,38(7):44-45.

[10] 王正林,刘明.精通MATLAB7[M].北京:电子工业出版社,2006.