利川市红椿沟日最大降雨量的GM(1,1)的预测与修正

秦文安,马友平

(1.恩施州水文水资源勘测局，湖北 恩施 445000;2.湖北民族学院 生物科学与技术学院，湖北 恩施 445000)

表1 原始数据、预测数据和相对误差表(mm)

降雨源于凝结的水蒸汽，水蒸汽的载体是大气流场，太阳辐照地表提供动力来源导致水蒸汽的产生.降雨量(以mm为单位)是指从天空降落到地面上的雨水，未经蒸发、渗透、流失而积聚的水层深度，它可以直观地表示降雨的多少.降雨量是最难以预报的气候变量之一，因为它涉及微观与宏观物理过程[1].降雨是水文水资源系统的输入，研究它特性，对于水文水资源系统的预报、模拟是十分重要的[2].众所周知，客观世界是物质世界，也是信息世界.信息完全不明确的系统为黑色系统，信息完全明确的系统为白色系统，信息部分不明确、部分明确的系统为灰色系统.历年的大气降雨量可组成一系统，在此系统中，过去的大气降雨量可通过测试获得，而未来的降雨量则不可知，因此该系统为一灰色系统，可以采用1982年，华中科技大学邓聚龙教授创立的灰色系统理论中的GM(1,1)模型对未来降雨量进行预测[3].为了对年最大日降雨量进行研究，选取了湖北省利川市红椿沟雨量站的观测数据，详见表1.

1 GM(1，1)灰色模型的基本原理

对某个事物发展变化的大小与时间所作的预测，称之为数据列.GM(1，1)[4-8]模型为单序列的一阶动态模型，是常用的一种灰色数列预测模型.

设原始无明显规律的时间序列{X(0)(i)}(i=1,2,…,n)作一次累加生成，得到序列：

X(1)={X(1)(1),X(1)(2),…,X(1)(n)}，

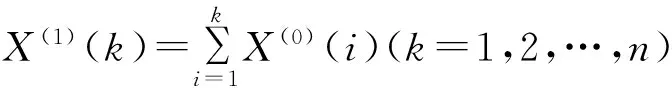
(1)

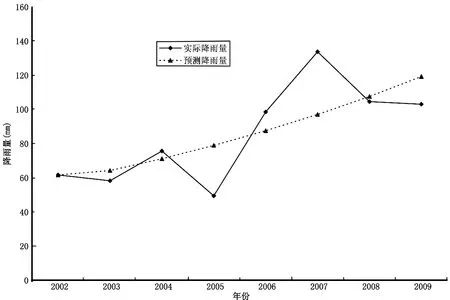
图1 日最大实际降雨量与预测值对比图

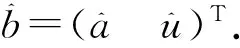
求解微分方程(1)式得时间响应模型:

可由最小二乘求解模型的参数a、u，即:

(2)

式中B为累加生成矩阵，Y为向量,二者的构造分别为:

Q=(X(0)(2),X(0)(3)，…，X(0)(n))T

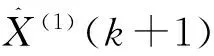
收集到的湖北省利川市红椿沟雨量站2002～2009年的观测数据如表1，由式(2)求得a=-0.103 3,u=54.532 4,可建立降雨量的预测模型为:

(3)

2 模型修正

修正采用区间预测法中的发展带模型，其适用于原始数据比较离散的情况，其基本原理如下[9].

构造新的序列:

建立GM(1,1)模型群：

由式(2)可得：

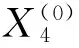
得最高预测值为：

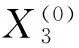
得到最低预测值：

由公式X(0)(n+k)=1/2(fU(n+k))可得基本预测值：

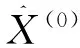
3 结果分析

模型修正的结果见表2，分别绘制了一次累加生成原值与发展带拟合图2.图3原始序列值与发展带模拟对比图.发展带与原模型预测对比图4.

表2 发展带预测模型原值、预测值计算结果(mm)

从图3可知一次累加序列原值与最高值最接近，图4也反映原模型预测值与发展带预测值最高值相近，因此可将最高值作为最终的预测结果.

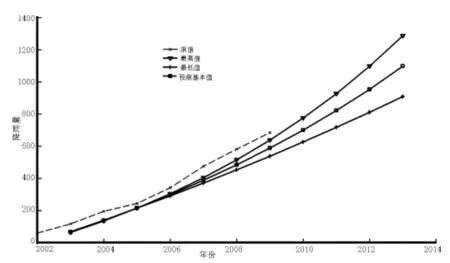
图2 一次累加序列原值与发展带模拟值对比

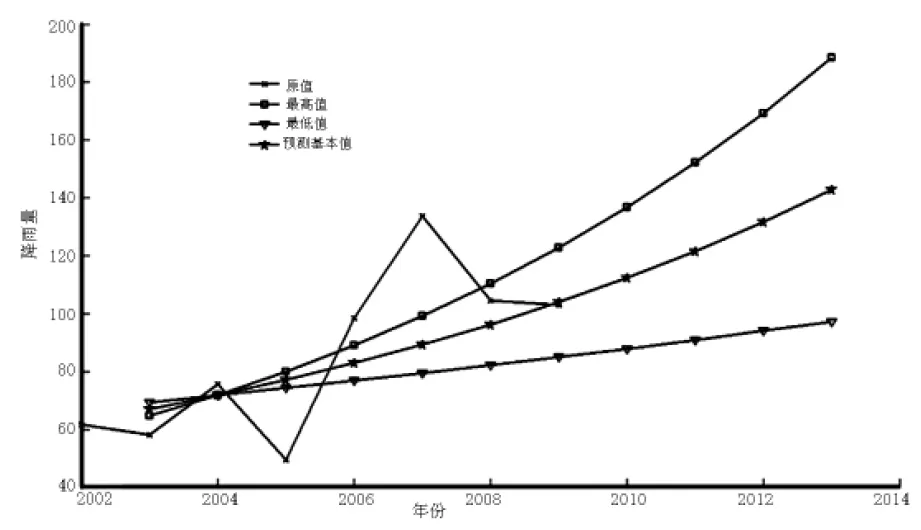
图3 原始序列原值与发展带模拟值对比

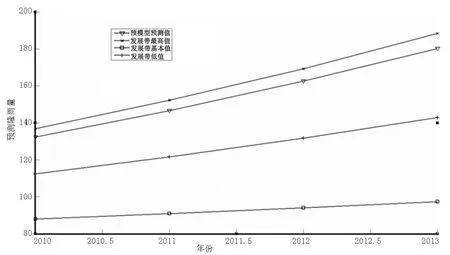
图4 原模型与发展带模型预测值对比

4 结束语

本文应用灰色理论中的GM(1，1)对年日最大降雨量进行分析，由于原始数据离散性太大，导致GM(1，1)的预测精度不太理想，通过修正发展带(群)模型的研究，可以最高值作为最终预测结果.

[1] 崔茂常,朱海.ECMWF再分析日降雨量与CMAP候降雨量在中国境内的数据整合[J].地球科学进展,2000,15(4):440-445.

[2] 袁鹏,李谓新,王文圣,等.月降雨量时间序列中的混沌现象[J]. 四川大学学报：工程科学版,2002.34(1):16-19.

[3] 傅鹤林,李亮,刘宝琛.降雨量预测理论模型及其工程应用研究[J].中国铁道科学,2002,23(4):62-66.

[4] 邓聚龙.灰理论基础工[M].武汉：华中科技大学出版社,2003:210-317.

[5] 邓聚龙.灰色系统基本方法[M].武汉：华中理工大学出版社,1998:100-150.

[6] 卢彦,刘勇,崔丽红.基于GM (1, 1)模型对齐齐哈尔市水土流失治理面积的预测[J].黑龙江水利科技,2006,34(6):131.

[7] 邓聚龙.灰色系统基本方法[M].郑州：河南大学出版社，1987：12-120.

[8] 马友平,张志华,艾训儒.城市化水平的灰色遗传算法预测[J].湖北民族学院学报：自然科学版,2008,26(1):68-71.

[9] 刘思峰,郭天榜,党耀国.灰色系统理论及其应用[M].北京：科学出版社,1999.