基于PCA和LDA融合的手写数字识别方法
张凯兵
(孝感学院计算机与信息科学学院,湖北孝感 432000)
通常,描述对象的元素很多,为了节省资源,节约计算机存储空间和提高识别效率,在保证识别率的要求下,按某种准则尽量选择对正确分类贡献较大的特征,使得提取的特征具有良好的分类性能。为此,很多情况下,需要对原始特征进行某种变换获得维数更少、分类能力更强的变换特征[1]。在模式识别系统中,特征的提取与选择是非常关键的步骤之一,一个成功的识别系统很大程度上依赖于特征的提取与选择[2-4]。特征选择是通过消除初始特征中相关的和冗余的信息,从而选择维数较低的并能反映模式分类信息的特征子集的过程。根据特征选择过程中是否使用类别信息可分为两类:监督特征选择和非监督特征选择。监督特征选择是一种通过互信息[5]或Fisher标准[6],从原始特征中消除噪声和不相关的信息,从而选择最具可分性特征的方法。而非监督特征选择方法主要度量特征间的相似性或相关性以消除冗余信息,在保证分类正确性的前提下降低特征维数[7]。特征选择是众多研究者一直关注的问题。近年来,同时考虑模式特征相关性和冗余性,将非监督特征选择和监督特征选择相结合的方法得到了广泛的应用[7-8],对提高识别率起到了积极的作用。同时,基于数据融合技术的模式识别技术能有效改善识别器的精度。文献[9]提出了使用主元分析(Principal Components Analysis,PCA)与线性鉴别分析(Linear Discriminant A-nalysis,LDA),获得 PCA-LDA的融合特征空间进行性别鉴别的方法。文献[10]针对SVD分类信息不足,提出了一种融合SVD和LDA特征进行人脸识别。PCA是一种常见的非监督数据降维方法,它将维数较高、彼此间存在一定相关性的原始特征变换成彼此不相关的但能反映原特征本质信息的低维特征。而LDA是一种监督特征选择方法,它在减低数据维数的同时还考虑不同类别模式间的类别信息,使得投影后的特征子空间在同类模式间类内散度最小化,而不同类别模式类间散度最大化,因此变换后的特征具有很强的可分性,但不能保证消除不同特征间的相关性和冗余性。本文结合PCA和LDA各自的优点,提出一种融合主成分分析(PCA)和线性判别分析(LDA)的手写数字识别新方法。该方法采用线性加权方案融合PCA和LDA特征,分别计算未知模式的PCA和LDA特征与训练样本的PCA和LDA特征间的距离,对两种距离进行加权平均后,采用最近邻分类器判别测试样本类别。对USPS样本库和自备样本库的实验结果表明,与单一的 PCA和LDA方法相比,利用 PCA和LDA融合方法能进一步提高识别正确率。
1 基于PCA和LDA的特征选择
1.1 PCA特征选择
主成分分析(principal component analysis)[11]是将分散在一组变量上的信息集中到某几个综合指标(主成分)上的统计分析方法。利用主成分描述数据集内部结构,起着数据降维作用,在模式识别中得到了广泛应用。PCA可将原始高维特征向量投影到一个低维子空间中,使得在平均误差最小化情况下能重构原向量。通过估计训练样本的协方差矩阵,计算其特征向量和特征值,对特征值进行排序,取最大的 k个特征值对应的特征向量作为子空间的基向量,将 k个基向量按列排列成变换矩阵W=[w1,w2,…,wk]。设 x是一个 d维向量是所有N个样本的均值,由y=WT(x-μ)可将原始d维征特征向量x变换成一个k维子空间中的向量y,且 k< d。
1.2 LDA特征选择
LDA[12]是一种有效解决模式分类问题中可分性的方法,通过将初始特征投影到一组最具可分性的投影轴上,使得分类模式在投影特征空间类间散度最大,类内散度最小。

第i类样本的均值μi估计为:

总体样本均值估计为:

第i类样本的协方差Si估计为:

则所有样本的类内散度矩阵和类间散度矩阵分别估计为:
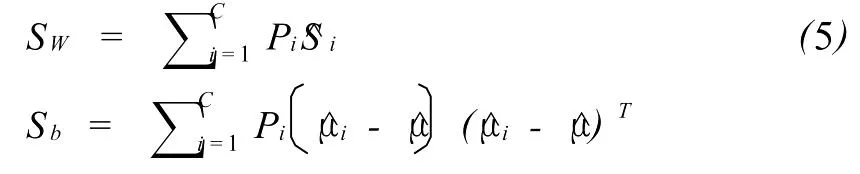
设矩阵Wm×n是将原始样本空间Rn向特征空间 Rm的投影矩阵。由于LDA要求类内散度最小而类间散度最大,则可定义如下成本函数:

最大化J(W)可得最优投影矩阵W,即

其中{wi}是Sb和SW的最大的m个特征值{λi}对应的广义特征向量。根据变换矩阵W,所求的特征向量=WT,i=1,…,C,j=1,…,ni。
2 基于PCA和LDA融合策略
考虑到PCA和LDA变换的特点,将两者进行融合能有效提高分类器的性能。融合的目的主要克服单个分类器或特征向量的不足,利用彼此间的互补性,从而进一步提高的识别系统的识别正确率。由于PCA能在降低原始特征维数的同时保留其本质信息,但不能保证变换特征的可分性,而LDA能减低原始特征维数的同时在最大限度地保持变换特征的可分性,但不能消除特征冗余信息,因此将两者融合可以优势互补,在消除冗余信息的同时能保持良好的可分性。
基于分类器融合主要目标是如何测度两个模式之间的最终距离。文献[13]在理论上分析了平均方案和乘积方案适用的条件。本文采用线性加权方案融合PCA和LDA特征,分别计算未知模式的PCA和LDA特征与训练样本的 PCA和LDA特征间的距离,然后对两种距离进行加权平均,采用最近邻分类器实现最终分类。融合过程如下:
2)计算未知模式与所有训练模式间的距离:



上式中,w是PCA与LDA之间融合的加权系数,其值是[0,1]之间的某个常数。显然,当w=0时,加权距离变为LDA分类结果;当w=1时,加权距离变为PCA分类结果。
4)根据计算的距离(di1,di2,…,diN)使用最近邻分类器进行分类决策:

3 实验结果与分析
采用美国邮政系统数据库USPS[14]和自备手写数字样本数据库[15]对提出方法进行实验。如图1是部分USPS样本。USPS样本库包括7291个训练样本和2007个测试样本,大小均为16×16的灰度图像。
除USPS样本库外,采集不同人和书写工具书写的数字样本构成自备样本数据库。如图2是部分自备样本。该样本库由9000个样本组成,其中训练集中有4000个样本,测试集中有5000个样本,每个样本归一化为48×48大小的二值图像,训练集和测试集中每类数字分别有400和500个样本。

图1 部分USPS手写数字样本

图2 部分自备手写数字样本
对USPS训练集中的7291个样本,将灰度数字图像点阵按行方向构成256维的原始向量,分别进行PCA和LDA的变换矩阵,将训练集和测试集中的样本变换到各自的特征子空间进行融合,最后采用最近邻分类器进行分类识别。
对自备样本库,先将规一化大小为48×48的二值图像进行细化,然后将字符图像点阵从水平和垂直方向平分为6等份,提取48维的粗外围特征。使用大小为8×8的网格将字符图像点阵分割成36等份,取每份中的黑色像素个数对整个字符黑色像素的比率,构成36维粗网格特征。将字符点阵向水平、垂直、45°、135°四个方向投影 ,每个方向取16个投影值,组成64维笔画密度特征。从水平、垂直、45°、135°四个方向对字符图像进行投影,构成12维笔画投影特征。将以上四类特征进行组合,构成160维的统计特征。对高维的统计特征,分别进行PCA和LDA变换,将训练集和测试集中的样本变换到特征子空间进行融合,最后采用最近邻分类器进行分类识别。表1是USPS样本库和自备样本库分别使用 PCA、LDA和PCA+LDA三种方法得到的识别率对照表。

表1 不同方法识别率对照表
为得到最优融合系数,对公式(11)中的加权系数取[0,1]之间的值,变化步长为0.1,分别得到两个实验数据库在不同融合系数下的识别率,变化曲线如图3所示。由图3可以看出,采用PCA+LDA的融合方法比单独的 PCA和LDA方法获得的识别率都要高,且当融合系数w=0.8时,获得最高的识别率。因此,与单独的 PCA和LDA识别方法相比,PCA+LDA的融合方法能有效性提高手写数字识别率。

图3 不同融合系数识别率变化情况
4 结论
针对PCA和LDA特征选择方法的优点与不足,提出一种在分类器层次上融合 PCA和LDA特征进行手写字符识别方法。对USPS样本库和自备样本库的实验结果表明,与单独的 PCA和LDA方法相比,本文提出的融合方法能获得更高的识别正确率。
[1] 模式识别中的特征提取与计算机是绝不变量[M].北京:国防工业出版社,2001.
[2] 朱小燕,史一凡,马少平.手写字符识别研究[J].模式识别与人工智能,2000(6):174-180.
[3] 马少平,周莹,朱小燕.基于模糊方向线索特征的手写体汉字识别 [J].清华大学学报:自然学科版,1997(3):42-45.
[4] 胡中山,娄震,杨静宇.基于多分类器组合的手写体数字识别[J].计算机学报,1999(4):369-374.
[5] Kwak N,Choi C.Input feature selection by mutual information based on Parzen window[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002(12):1667-1671.
[6] Duda R,Hart P,Stork D.Pattern recognition[M].California:John Wiley&Sons,2000.
[7] Mitra P,Murthy C,Pal S.Unsupervised feature selection using feature similarity[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002(3):301-312.
[8] Peng H,Long F,Ding C.Feature selection based on mutual information criterion of max-dependency,max-relevance,and min-redundancy[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(8):1226-1238.
[9] 何国辉,甘俊英.PCA-LDA算法在性别鉴别中的应用[J].计算机工程,2006(19):208-210,213.
[10] Pang Yanwei,Yu Nenghai,Zhang Rong et al.Fusion of svd and lda for face recognition[C].International Conference on Image Processing,2004,2:1417-1420.
[11] Jolliffe I.Principal Component Analysis[M].Newyork:Springer-Verlag,1986.
[12] Belhumeur P,Hespanha J,and Kriegman D.Eigenfaces vs.fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997(7):711-720.
[13] Tax M,Breukelen M,Duin R,Josef K.Combining Multiple Classifiers By Averaging Or By Multiplying[J].Pattern recognition,2000,33:1475-1485.
[14] USPS Handwritten Digit Database[OL].http://www.cs.toronto.edu/roweis/data.html.
[15] 张凯兵,宋俊典,邓立国.手写字符样本自动采集研究[J].四川工业学院学报,2004(S1):41-43.

