基于模式匹配法的布拉格光栅仿真研究

陈 欢 ,汤 斐

(孝感学院物理与电子信息工程学院,湖北孝感432000)

模式匹配法是一种利用传输矩阵、散射矩阵和完全匹配层直接求解电磁场边值问题的方法。它不同于时域有限差分法的网格分析模式,对横向结构相同的光波导,在每个层面上用同一个矩阵进行描述,因此计算速度快,尤其适合于大型光波导集成器件的计算,是一种非常有前景的数值模拟方法。在周期性结构和多层介质材料、变折射率光学集成器件中得到了广泛的应用。

用模式匹配法求解一个复杂光波导器件中的光场分布时,可以将光波导器件沿纵向方向把它分割成很多小段,每小段内光波导的横向结构和折射率分布近似不变,因此其内部的光场分布可以用其本征解的叠加来表示。而在两段光波导连接处,根据光场的连续性可以从一侧的本征模系数推导出另一侧的本征模系数,此即模式匹配法的核心思想[1]。

1 模式匹配法

图1表示相邻两段波导Ⅰ和Ⅱ的分界面。在介质 Ⅰ中沿方向有一个p阶入射模,该入射模式在波导 Ⅰ和 Ⅱ的分界面发生反射,在介质 Ⅰ中形成一个反射场,同时在介质 Ⅱ中形成一个透射场。我们将反射场和透射场分别用介质 Ⅰ和 Ⅱ中的本征模展开来表示[2],根据光场的切向分量连续性得到如下方程:

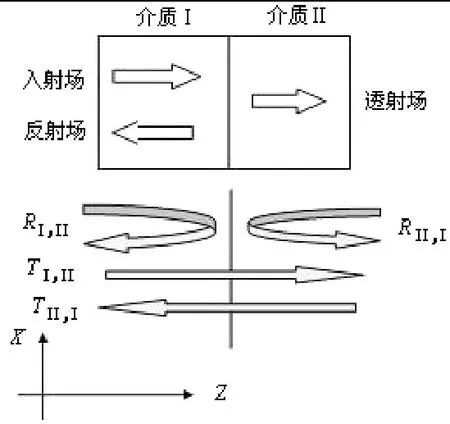
图1 相邻两段波导的分界面

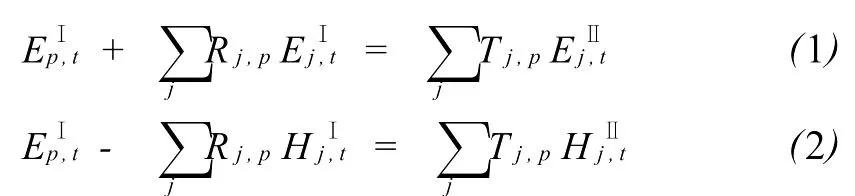
磁场 H中的负号是根据本征解相对应的反向传输本征解而得到的。式中的展开系数 Rj,p和Tj,p分别称为反射系数和透射系数。将(1)式右边叉乘,将(2)式左边叉乘。这里,i表示介质Ⅰ或介质 Ⅱ。再记重叠积分为:

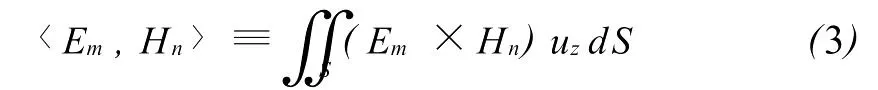
可以得到:

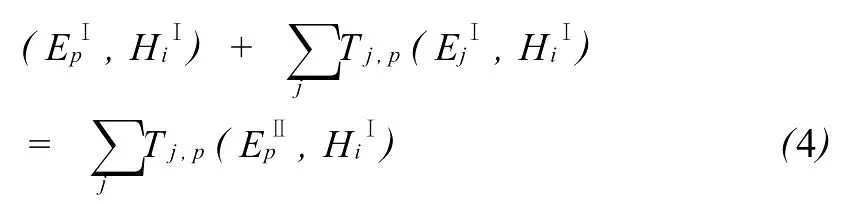
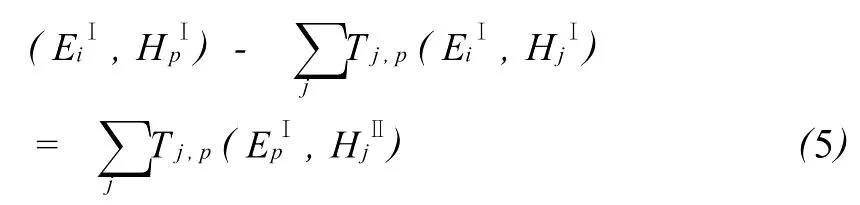
进一步可利用正交关系式

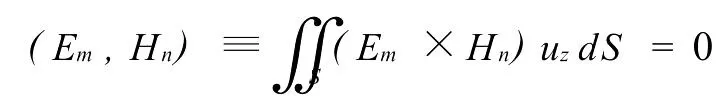
将(4)式和(5)式化简为:

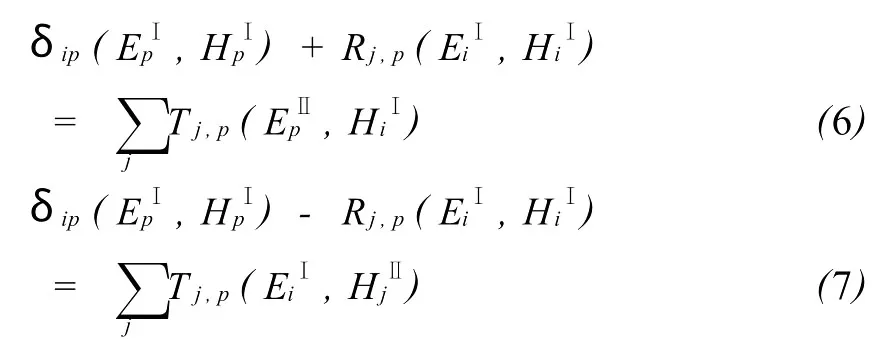
加减这些场方程得到:

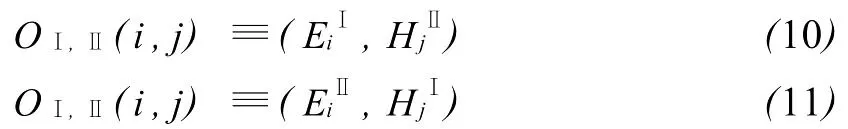
在(8)式和(9)式中,列出 p从1→N的所有方程,最后得到:

在上述两个表达式中 TⅠ,Ⅱ和RⅠ,Ⅱ称为透射矩阵和反射矩阵,角标 T表示转置矩阵。如果用列向量Ainc表示任意一个入射波的本征模展开系数Ainc,则反射场和透射场可以写为:

这样就得到了从介质 Ⅰ到介质 Ⅱ的反射矩阵 RⅠ,Ⅱ和透射矩阵 TⅠ,Ⅱ,利用同样的办法可以得到从介质 Ⅱ到介质 Ⅰ的反射矩阵RⅡ,Ⅰ和透射矩阵 TⅡ,Ⅰ。综合这四个矩阵就可以描述相邻两断波导界面处的光场分布情况。在采用模式匹配法的计算过程中所取用的本征模的个数越多,计算结果就越精确,但随之而来的计算量也越大。

2 布拉格光栅仿真研究

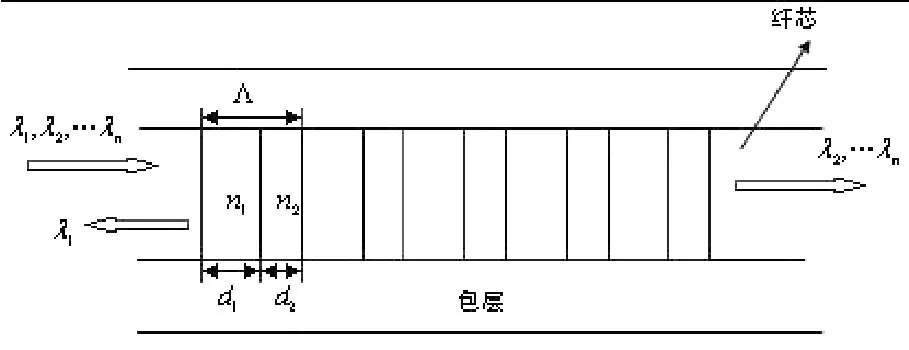
图2 布拉格光栅结构图

根据上述讨论,对布拉格光栅来进行仿真模拟。根据布拉格光栅的结构图(见图2),设入射光λ=1.5102μm,n1=1.53,n2=1.52。计算在 d1段对应的光波导中的第一个导模的值β1=6.2811302878867;同样计算在 d2段对应的光波导中的第一个导模的值β2=6.31177186060469。取 d1=2.5π/β1=1.2504,d2=2.5π/β2=1.2443,用512个周期进行计算布拉格光栅的反射率和透射率,得到图3。其中实线代表反射率,虚线代表透射率。从图3中可以看出,该布拉格光栅的反射带宽为1.3 nm。

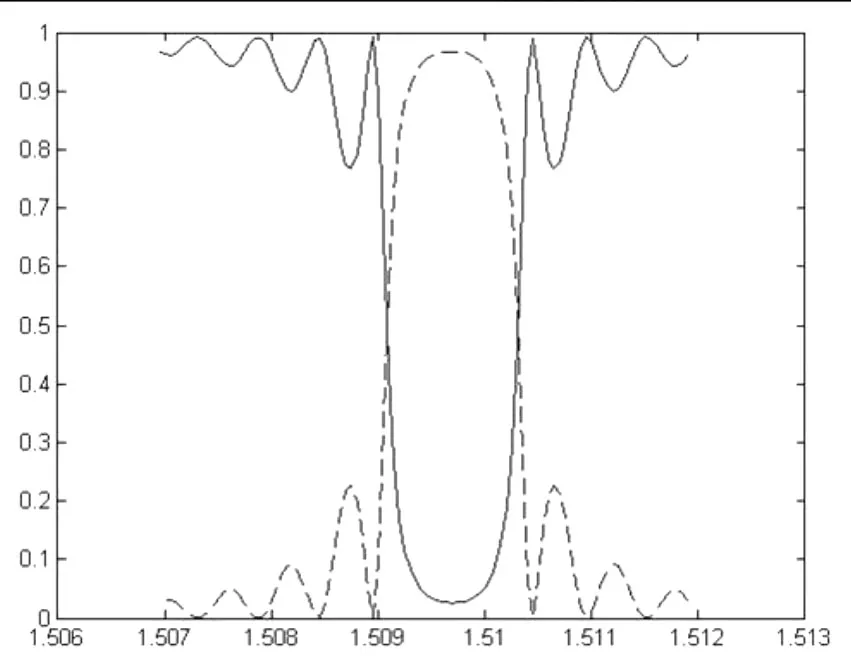
图3 布拉格光栅的反射率与透射率特性

记Δn=|n1-n2|,对比计算两个布拉格光栅,第一个布拉格光栅的折射率分别为 n1=1.52和 n2=1.53,Δn=0.001;第二个布拉格光栅的折射率分别为n1=1.52和n2=1.521,Δn=0.001。设定好布拉格光栅的周期和长度,使其反射率都接近1,分别在其中心波长附近进行计算,得到图4,我们看到,Δn=0.001的布拉格光栅的反射带宽为1.3 nm,而Δn=0.001的布拉格光栅的反射带宽仅为0.4 nm。当折射率差增大时布拉格光栅的反射带宽增大。

为了分析布拉格光栅中周期数对反射率的影响,设入射光λ=1.5μm,n1=1.53,n1=1.52,d1=1.2504,d2=1.2443。采用模式匹配法取256个周期和512个周期在中心波长附近进行计算,得到图5。这时取256个周期时,布拉格光栅的反射率最大也只有70.34%,当取512个周期时,布拉格光栅的反射率近似为1。也就是说,当布拉格光栅的周期长度增加时反射峰值增大。

图4 折射率差对布拉格光栅反射率的影响

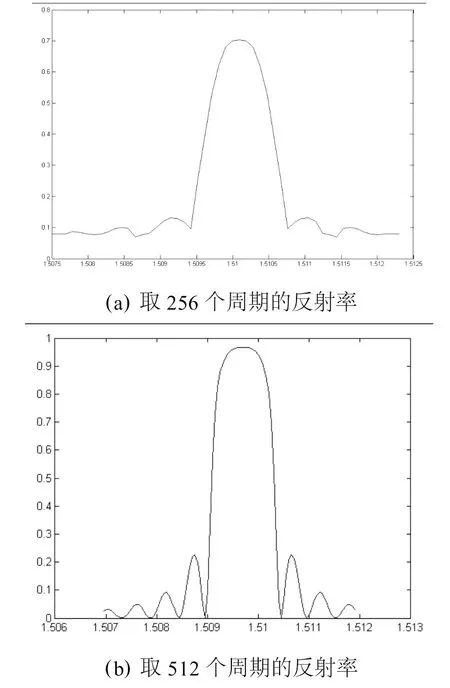
图5 布拉格光栅的周期数目对反射率的影响

根据图2,设入射光λ=1.5102μm,n1=1.53,n1=1.52,d1=1.2504,d2=1.2443,用512个周期计算反射率接近1的光场分布见图6。

改变入射光的波长λ=1.5102μm,其他条件不变得到图7的光场分布图。此时透射率接近1。可看到从右至左,反射光时大时小,无法有效的累积叠加,因此总反射光很弱(最大约0.5)而透射很强(大约10)。

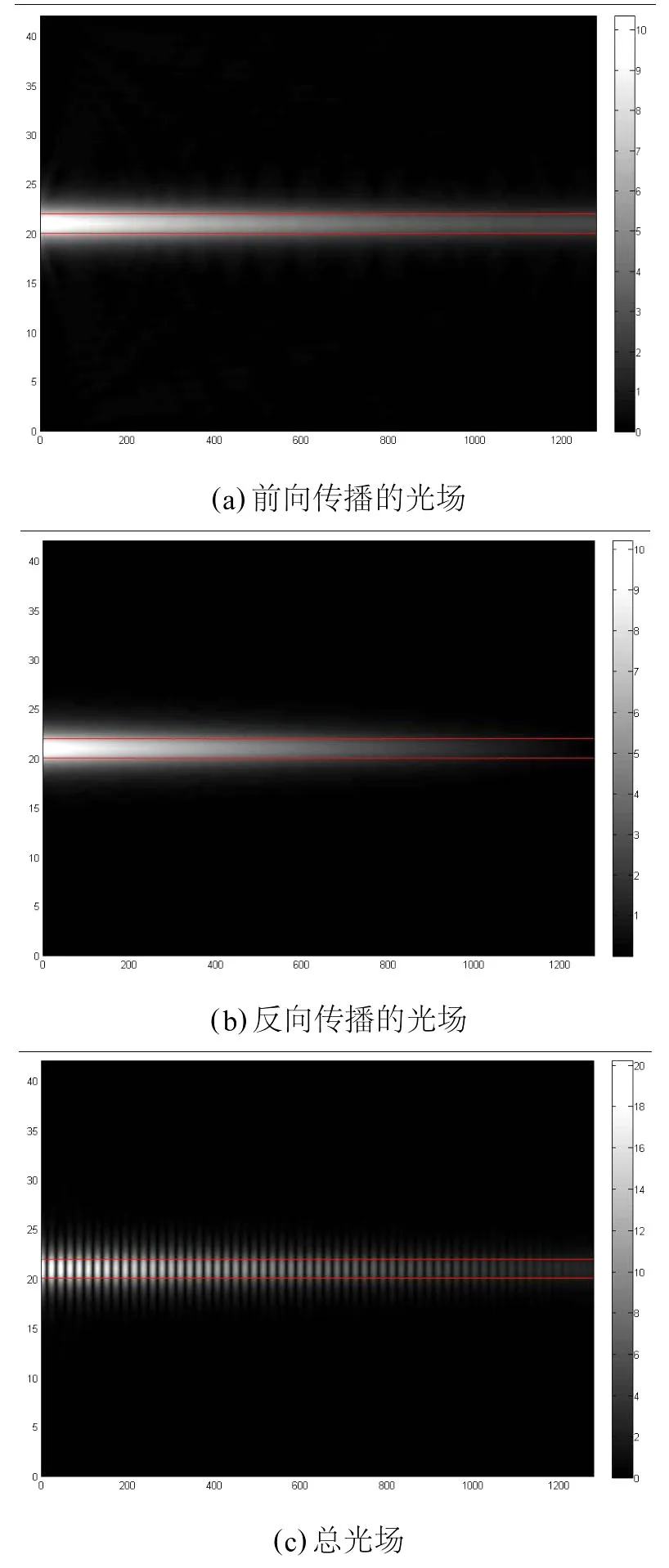
图6 布拉格反射器中的光场分布

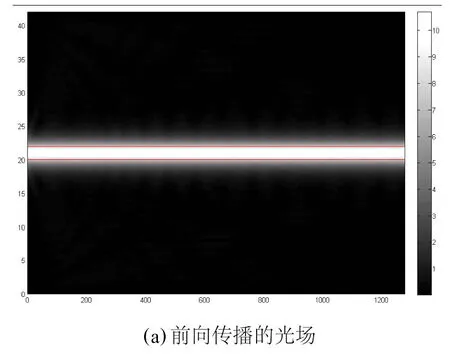
图7 布拉格滤波器中的光场分布

3 结论

本文讨论了模式匹配法的基本理论框架,并利用MA TLAB编程对不同结构参数的布拉格光栅进行了仿真模拟,发现当折射率差增大时布拉格光栅的反射带宽增大,而当布拉格光栅的周期长度增加时反射峰值增大,这些行为特征与传统耦合波理论分析相一致。我们相信这些结论对布拉格光栅的设计具有一定的帮助。

[1] Bienstman P,Baets R.Waveguide and resonator modeling based on ectorial eigenmode expension and perfectly matched layer boundery conditions[Z].Progress In Electromagnetics Research Symposium-PIERS 2000.United States,2000.

[2] Berenger J P.A perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics,1994(2):185-200.