n阶常系数线性非齐次微分方程特解的统一求法

陈华喜

(蚌埠学院 数理系,安徽 蚌埠 233030)

n阶常系数线性非齐次微分方程特解的统一求法

陈华喜

(蚌埠学院 数理系,安徽 蚌埠 233030)

关于n阶方程 y(n)+a1y(n-1)+…+an-1y′+any=f(x)的特解的求法,大多是对右端函数的f(x)按分成3种类型 ,设定相应的特解函数 ,然后利用待定系数法进行求解,方法较为繁琐。文章采用了较为初等的方法,对 f(x)的3种不同类型的求解进行了统一。

线性微分方程;求导;特解

形如

的方程称为n阶常系数非齐次线性微分方程,其中a1,a2…,an为常数,而 f(x)为连续函数.若f(x)=0,则方程(1)变为

称其为方程(1)对应的齐次方程。

方程(1)的通解,等于方程(2)的通解与方程(1)的一特解之和,方程(2)的通解易求,因此,要求(1)的通解,关键是求(1)的一特解。目前,国内《常微分方程》文献中大多是将f(x)分为Pm(x),(其中 Pm(x)为 m次多项式,而为次数不高于m次的多项式,但二者至少有一个的次数为m)三种情况,分别按各种类型设定相应的特解函数,用待定系数法求解,方法较为繁琐,而且难以记忆。

本文对上述方程右端函数的3种类型进行了统一求解,方法简单、容易记忆。

1 类型 Ⅰ

当 f(x)=Pm(x)(Pm(x)为 m次多项式)时,则方程(1)为

两边关于 x依次求m次导有:求1次导得:

求2次导:

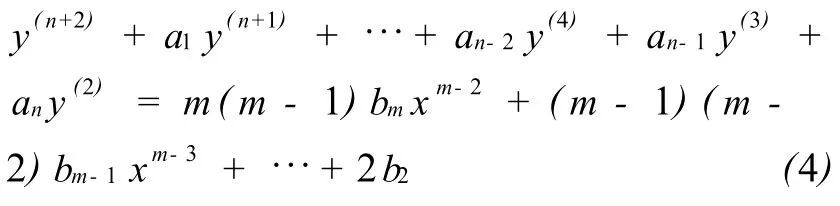
求m-1次导:

求m次导:

由于方程(1)的解为不高于 m次的多项式,故 y(n+m)=y(n+m-1)= …=y(m+2)=y(m+1)=0,因而在(6)式中令 any(m)=m!bm,即得 y(m)=!,将 y(m)带入(5)可求得 y(m-1),再将 y(m),y(m-1)带入上一级可得y(m-2),依次下去,最终可求得y。

例1求方程

的特解。

解:对方程两端分别关于 x求三阶导有:

求一阶导得:

求二阶导得:

求三阶导得:

由于 y(6)=y(5)=y(4)=0,故令6y(3)=6,得

代入(8)有

再将(10),(11)代入(7)得

最后将(10),(11),(12)代入原方程得

2 类型 Ⅱ

当 f(x)=Pm(x)eλx时 ,则方程(1) 为

令 y=u(x)eλx为其特解,代入原方程消去 eλx后得:

(其中 f(λ)为原方程得特征多项式)方程为关于u(x)的n阶方程,由类型I的解法可求出u(x),从而求得原方程得特解 y。

例2求方程

的特解。

解:令

则

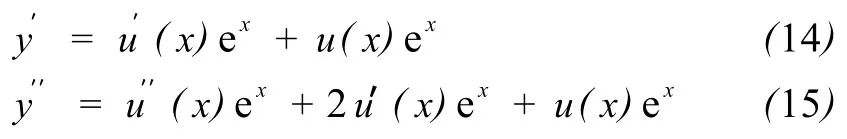
将(13),(14),(15)代入原方程得:

将方程(16)两端分别关于 x求两阶导有:求一阶导得:

求二阶导得:

由于 u(4)(x)=u(3)(x)=0,故令 20u′′(x)=2,得

代入(17)有

再将(19),(20)代入(16)得

原方程的特解为:

3 类型 Ⅲ

由叠加原理知,上述方程的特解 y等于求方程

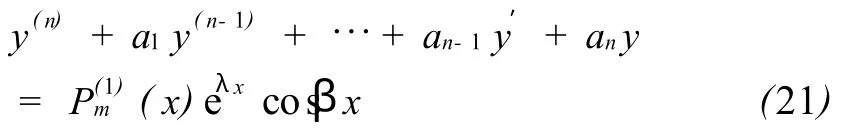
的特解

的特解 y2之和,即 y=y1+y2。

对于方程(21)可求方程z(n)+a1z(n-1)+…+an-1z′+anz=的特解z(z解法同类型 Ⅰ),z的实部就是方程(21)的特解 y1,同理方程(22)的特解 y2也可求得,从而便知原方程得特解 y。

例3求方程 y′′-2y′+2y=x excos x的特解。

解:求原方程的特解等价于求方程

的特解的实部。令

则

将(24),(25),(26)代入原方程得:

对方程(27)两端关于 x导得:

令 2i u′′(x)=1,得

代入(27)有

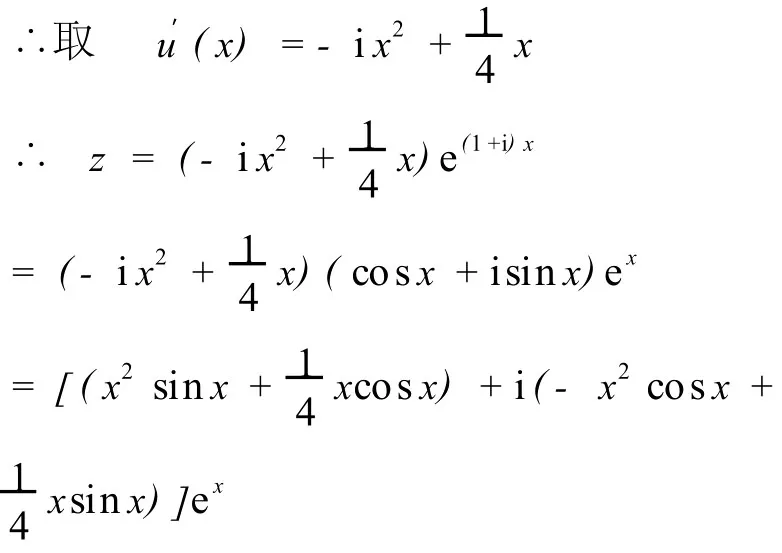
∴原方程的特解为:

由此可见,这里所介绍的求高阶方程特解,不再用待定系数法根据方程右端函数 f(x)的不同种类进行求解,而是用了一种较为初等的方法求解方程的特解,这种方法将方程右端函数的不同种类进行了统一,易于理解和记忆。

[1] 王高雄,周之铭,朱思铭,等.常微分方程[M].3版.北京:高等教育出版社,2006.

[2] 黄启昌,周之铭,等.常微分方程[M].北京:高等教育出版社,2001.

[3] 佘智君.二阶常系数非齐次线性微分方程通解的简易求解法[J].重庆工学院学报,2008(8):85-86.

[4] 杨国梁,周周,杨志勇,等.二阶常系数非齐次线性微分方程特解的一种求法[J].内江师范学院学报,2009(S1):248,250.

The Uniform Solution to n Order Constant Coefficient Non-homogeneous Linear Differential Equation

Chen Huaxi
(Department of Mathematics and Physics,Bengbu College,Bengbu,Anhui 233030,China)

About the solutions to the n order equations y(n)+a1y(n-1)+ …+an-1y′+any=f(x),most classify the function f(x) into three types according to Pm(x),Pm(x)eλx, ((x)cosβx +(x)sinβx)eλx,set appropriate particular solution function,and then solve the equation using undetermined coefficient method.These solutions are more complicated.In this paper,the author adopted a more elementary method to solve the equation and the solutions to three different types of f(x)were unified.

linear differential equations;derivation;particular solution

O175

A

1671-2544(2010)06-0026-03

2010-08-08

陈华喜(1977—),男,安徽淮南人,蚌埠学院数理系讲师,硕士。

(责任编辑:陈 鑫)