一类正项级数收敛判断的推广

徐国进,徐国安

(1.孝感学院数学与统计学院,湖北孝感432000;2.孝感市孝南区朋兴中学,湖北孝感432000)

一类正项级数收敛判断的推广

徐国进1,徐国安2

(1.孝感学院数学与统计学院,湖北孝感432000;2.孝感市孝南区朋兴中学,湖北孝感432000)

主要利用正项级数的收敛原则以及Cauchy不等式、Holder不等式得出了判断一类正项级数收敛的方法,并对该方法进行了推广。

正项级数;收敛;发散

1 引言及引理

正项级数的收敛问题是数学分析课程中的一个重要内容,正项级数的收敛判别方法也多种多样,本文旨在探讨一类正项级数

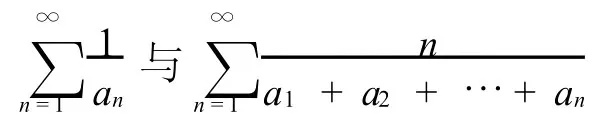
之间的收敛关系,从中得出一些新的判别方法,对此类正项级数的收敛判断作一个补充,并给出其应用案例。

为便于讨论和证明,先列出本文涉及到的部分引理。

引理1[1,4](部分和有界,正项级数收敛) 正项级数∑un收敛的充要条件是:部分和数列{sn}有界,即存在某正数 M,对一切正整数 n有sn＜M。

引理2[1,4](比较原则) 设 ∑un和 ∑vn是两个正项级数,如果存在某正数 N,对一切n＞N都有 un≤vn,则1)若级数 ∑vn收敛,则级数∑un也收敛;2)若级数 ∑un发散,则级数 ∑vn也发散。

引理3[3](Cauchy不等式) 设 ai,bi为任意实数(i=1,2,…,n),则

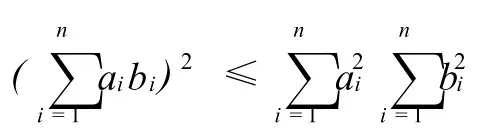
其中等号当且仅当ai与bi成比例时成立。

2 主要结论及其证明

定理1若0＜a1≤a2≤…an≤an+1≤…,则收敛的充要条件为如下级数收敛。

证明1)充分性。

n≥2时,由

2)必要性。

所以,对一切正整数 N,存在某正整数 M,有

(上述证明中,[x]为 x的取整)

定理2若正项级数收敛,那么正项级数收敛。

证明因为收敛,得

所以,任给正数ε,总存在正整数 N,使得当 n＞N时,有即 an＞,将数列{an}按递增排序,记它为{bn},此时存在正整数 N0,当n＞ N0时,有 bn≤an,从而因重新排序不改变级数的收敛性,故收敛,再由定理1,收敛,又根据引理2比较原则,正项级数收敛,证毕。

定理3设为收敛正项级数,则存在常数k使

证明由引理3Cauchy不等式:

定理4若正项级数收敛,则正项级数收敛。

证明设sn=a1+a2+…+an,s0=0,

问题:把定理4进一步推广一下,还能不能得到类似的结果呢?

定理5若正项级数是收敛的(其中p为常数,且 p＞1),则正项级数收敛。

证明设sn=a1+a2+…+an,s0=0,则

[1] 华东师范大学数学系.数学分析[M].3版.北京:高等教育出版社,2001.

[2] 任亲谋.数学分析习题解析[M].西安:陕西师范大学出版社,2004.

[3] 裴礼文.数学分析中的典型问题与方法[M].2版.北京:高等教育出版社,2006.

[4] 陈传璋,金福临,朱学炎.数学分析[M].2版.北京:高等教育出版社,1983.

[5] 吉米多维奇.数学分析习题集[M].北京:人民教育出版社,1979.

The Extension of Convergence Tests for a Class of Series of Positive Terms

Xu Guojin1,Xu Guoan2
(1.School of Mathematics and Statistics,Xiaogan University,Xiaogan,Hubei 432000,China;2.Pengxing Middle School of Xiaonan District,Xiaogan,Hubei 432000,China)

By use of convergence principles,Cauchy inequality and Holder inequality,several methods of finding the convergence of a class of series of positive terms are given in this article.Also,these methods are extended.

series of positive term s;convergence;divergence

O173.1

A

1671-2544(2010)03-0023-03

2010-03-12

湖北省教育科学“十一五”规划项目(2007B086)

徐国进(1964— ),男,湖北孝感人,孝感学院数学与统计学院讲师。徐国安(1961— ),男,湖北孝感人,孝感市孝南区朋兴中学教师。

(责任编辑:周 游)