中间λ康托集上可积函数空间的可分性
胡晓梅
(咸宁学院数学与统计学院,湖北咸宁 437100)
中间λ康托集上可积函数空间的可分性
胡晓梅
(咸宁学院数学与统计学院,湖北咸宁 437100)
通过一类特殊的分形集——中间λ康托集的构造,得到它的一些重要拓扑性质和分形特征,进而利用Stone-Weierstrass定理,证明了中间λ康托集上 P方可积函数空间是可分的。
中间λ康托集;可积函数空间;可分性
1 预备知识
定义1(IFS) 设(Rn,d)为n维欧氏空间,如果对任意i∈{1,2,…,N},fi:Rn→Rn是压缩映射,即对任意 x,y∈Rn,存在 r1∈(0,1),使得d(fi(x),fi(y))≤rid(x,y),则称压缩映射族{fi}为(Rn,d)上一个迭代函数系统。如果上式取等号,则称 fi为相似压缩映射。
Hutchinson已证明对于给定的 IFS{fi},必存在唯一非空紧集 K⊂Rn满足称 K为关于迭代函数系统{fi}的不变集或吸引子[2]。例如由相似压缩迭代函数系统生成的不变集 C就是通常意义下的三分Cantor集。它是一个自相似集[3]。
定义2设一非负集函数μ:{A:A⊂X}→[0,∞]满足
1)μ(φ)=0;
对于给定的IFS{f1,f2…,fN}和满足pi>0,1≤i≤N的概率向量 P=(p1,p2,…,pN),Hutchinson在文献[2]中已证明存在唯一的μ∈U,使得对任意的Borel集 A,有μ(A)=称满足上式的测度为关于IFS和P的不变测度。
特别地,当上述IFS是一族相似压缩映射时,此测度就称为关于它们的自相似测度。
定义 3设 f(x)是 F上的可测函数,记其中 F为中间λ康托集,μ为关于IFS和P=(1/2,1/2)的自相似测度。用 Lp(F,μ)表示‖f‖p< ∞的函数 f的全体组成的函数空间。
显然Lp(F,μ)是线性赋范空间,‖.‖p为其范数。
定义4设г是Lp(F,μ)中的子集,若对任意的 f∈Lp(F,μ)以及ε>0,存在 g∈г使得 ‖f-g ‖ <ε,则称 г在Lp(F,μ)中稠密。若 Lp(F,μ)中存在可数稠密子集,则称Lp(F,μ)是可分的。
2 中间λ康托集F的构造及性质
考虑闭区间 E0=[0,1]。
将 E0=[0,1]正中间去掉一个长度为原区间长度的λ(0<λ<1)倍的开区间剩下两个闭区间记E1为它们的并;再把E1中的这两个闭区间正中间分别去掉长度为它们各自区间长度的λ倍的开区间,得到集合 E2;然后将 E2中余下的四个闭区间同法处理得到集合 E3,如此继续下去,每一步都去掉区间中间一段比例为λ的部分,在第k步我们得到2k个长度为的闭区间,其并记为 Ek,当k→∞时,序列 Ek的极限集就是我们所构造出的中间λ康托集 F。显然,三分Cantor集为 F在λ时的特例。
由上面中间λ康托集F的构造容易得到F具有如下几条重要的性质:
1)是非空有界闭集;
2)是完全集;
3)无内点,即是无处稠密集;
4)完全不连通;
3 Lp(F,μ)的可分性及证明
引理1[4](控制收敛定理) 设{fn}是可测集 X上的可测函数列,μ是X上的测度。如果存在非负函数 g(x)∈(X,μ)满足
2)对所有的x∈X和任意的n,有 ︱fn(x)︱≤g(x),则 f ∈L(X,μ),且

命题1设1≤p≤∞,则任给 f∈Lp(F,μ),均存在Lp(F,μ)中的简单函数列使得当n→∞时,Sn几乎处处收敛到f,并且 ‖fsn‖p→0和
引理2[4](Lusin’s定理) 设 f(x)是可测集X上的可测函数,μ为 X上的测度。令 A={x∈X︱f(x)≠0},如果μ(A)< ∞,则任给ε>0,均有G∈Cc(X)使得μ({x∈X︱f(x)≠g(x)})<ε,并且经过适当选取有
引理3[5](Stone-Weierstrass定理) 设 Ω是Rd中的一个紧子集,令表示全体实系数d个变量的多项式全体,则在 C(Ω,R)中稠密,即对任意 f∈C(Ω,R)均存在d个变量的实系数多项式无限的逼近。
由于 C(F,R)满足该定理的条件,从而 F上实系数多项式在C(F,R)中稠密。另外因为任给一个实数均可以由有理数来逼近,即每一个实系数多项式均存在一有理系数的多项式来逼近,这即说明了 F上有理系数多项式全体在C(F,R)中稠密。
定理C(F,R)在 Lp(F,μ)中稠密,且Lp(F,μ)为可分空间(1≤p≤∞)。
证明令S表示 F上所有可测简单函数全体,因为μ(F)=1,从而μ({x︱s(x)≠0})< ∞。我们首先证明 S在Lp(F,μ)中稠密。显然 S⊂Lp(F,μ),我们先设 f> 0,由命题1知存在 F上的可测简单函数列{sn}几乎处处收敛于 f,并且0≤sn≤f。从而sn∈Lp(F,μ),这也即说明了sn∈S。又 ︱f-sn︱p,则由引理1的控制收敛定理,当n→∞时,‖f-sn‖p→0。对于一般的 f,因为f(x)=f+(x)-f-(x),这里
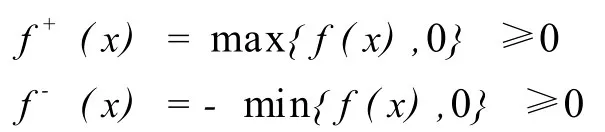
因此我们分别再对 f+(x)和 f-(x)作上面相同的论证 ,即存在和按照范数 ‖. ‖p分别收敛到 f+(x)和 f-(x)。令

综上,S在Lp(F,μ)中稠密。再来证 C(F,R)在Lp(F,μ)中稠密。设s∈S,对于任给的ε>0,由引理2的Lusin’s定理知,存在 g∈C(F,R)使得μ({g(x)≠s(x)}),并且适当选择有。因此,

又由Minkowski’s不等式得

这即说明了 C(F,R)在 中稠密。最后证Lp(F,μ)为可分空间。由引理3知 F上有理系数多项式全体在C(F,R)中稠密,而 C(F,R)在 Lp(F,μ)中稠密,故 F上有理系数多项式全体在Lp(F,μ)中稠密,而所有有理数全体是可数集,从而空间Lp(F,μ) 可分。
[1] 胡晓梅.三分Cantor集上 p方可积函数空间Lp(C,μ)的可分性.佳木斯大学学报,2008,26(6).
[2] Hutchinson J E.Fractal and Self-similarity[J].Indiana Univ M ath,1981,30(5):713-747.
[3] Falconer K J.Fractal Geometry:Mathematical Foundation and App lications[M].New York:John Wiley and Sons,1990.
[4] Rudin W.实分析与复分析[M].北京:机械工业出版社,2004.
[5] M cdonald J N,Weiss N A.A Course in Real Analysis[M].北京:世界图书出版公司,2005.
Separability of the Space of Integrable Function on the MiddleλCan tor Set
Hu Xiaomei
(School of Mathematics and Statistics,Xianning University,Xianning,Hubei 437100,China)
By analyzing the construction of the middleλCantor set,a typical fractal set,this paper discussed some topological properties and fractal characters of the middleλCantor set firstly,and then p roved that the space of integrable function Lp(F,μ)(1≤p≤∞)is separable by using the Stone-Weierstrass theorem.
the middleλCantor set;space of integrable function;separability
O177
A
1671-2544(2010)03-0026-03
2009-11-02
咸宁学院科研项目(ky09060)
胡晓梅(1979— ),女,湖北咸宁人,咸宁学院数学与统计学院讲师,硕士。
(责任编辑:周 游)

