一维常系数对流方程的步长定律和固有差分格式
李 娟
(北京理工大学机电学院,北京100081)
一维常系数对流方程的步长定律和固有差分格式
李 娟
(北京理工大学机电学院,北京100081)
由常用差分格式得出的差分余项中的奇数次幂项和偶数次幂项分别会产生弥散(色散或频散)和耗散效应。但是利用泰勒展开式并且使差分余项为零,可以得出一维常系数对流方程的步长定律和固有差分格式,结论也适用于解类似的变系数双曲型方程和拟线性双曲型方程。
偏微分方程;双曲型方程;对流方程;数值解法;差分格式
双曲型方程的一些常用数值解差分格式得出的差分方程会有差分余项存在,因此差分格式计算出的数值解有误差。虽然可以采用更复杂、精度更高的差分格式来降低误差,但是这样仍然存在计算量大和误差这两个问题,所以有必要寻求完全表示原微分方程的差分方程。通过利用泰勒(Taylor)级数展开[1],并且促使差分余项为零,可以解决因差分余项引起的弥散(色散或频散)和耗散效应,使数值解与解析解保持一致。
1 Lax-Friedrichs差分格式的泰勒(Taylor)级数展开
一维常系数对流方程:

其中u=u(x,t),a为常数且不为零。Lax-Friedrichs差分格式[2]:
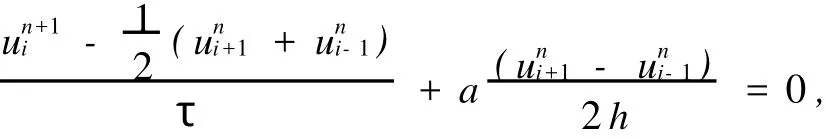
其中,τ为时间步长,h为空间步长。即得:

设u=u(x,t)是原微分方程(1)的光滑解,并且都在u(xi,tn)处由泰勒级数展开得:

将上述三式代入(2)式中,并整理得:
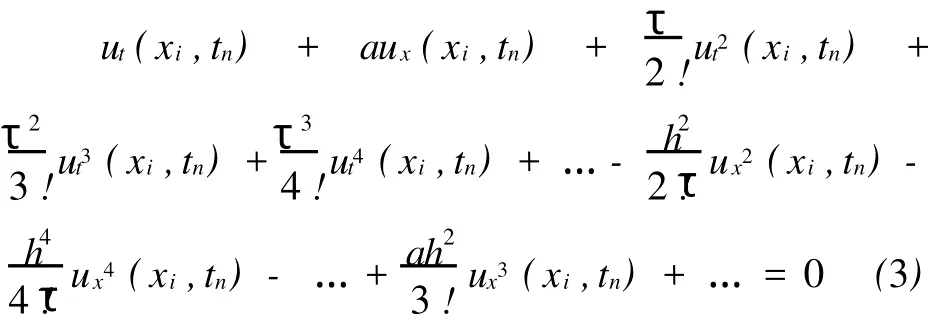
2 差分余项的消除
由原微分方程(1)得:

将(4)式代入(3)中,并整理得:


R(xi,tn)即为差分余项。当a2τ2-h2=0时,R(xi,tn)=0,那么由差分方程(2)式得到的微分方程(5)等价于原微分方程(1)。分别将aτ=h和aτ=-h代入(2)式中得:当aτ=h时,=;当aτ=-h时,。实际上,也可以通过采用这种方法对迎风格式(upwind)、Lax-Wendroff格式和Beam-Warming格式进行分析从而得出相同的结果。
3 结论
一维常系数对流方程的固有差分格式:

对于∂u/∂t+a(x,t)∂u/∂x=0这样的变系数双曲型方程,虽然特征线dx/dt=a(x,t)是一条曲线,但是u的值沿特征曲线保持不变,所以若已知a(x,t),那么将同一条特征线上相邻两时刻点的相对斜率(△x/△t)作为当前步长内的常数a值,在每步内看作常系数双曲型方程,这样计算出的值即为准确解。对于∂u/∂t+u∂u/∂x=0这样的拟线性双曲型方程,满足a=u0,即由初值确定常数a的一系列不同的一维对流方程,每一点仍可用常系数对流方程来解。
4 应用
例 设方程

满足边界条件:u(1,t)=u(111,t)=0和初始条件:

解 选取τ=h=a=1,依据一维常系数对流方程的固有差分格式得t=0、t=43和t=86时x轴上各点的u值分别如图1、图2和图3所示。

图1 t=0时各点的u值

图2 t=43时各点的u值

图3 t=86时各点的u值
5 总结
本文得出一维常系数对流方程数值解法的步长定律和固有差分格式,解决了其他差分格式因差分余项带来的误差,结果对于解类似的简单变系数双曲型方程和拟线性双曲型方程也适用。实际上,差分方程稳定与不稳定的边界就是原微分方程。
[1] 恽寿榕,涂候杰,梁德寿,等.爆炸力学计算方法[M].北京:北京理工大学出版社,1995:63-65.
[2] 陆金甫,关治.偏微分方程数值解法[M].2版.北京:清华大学出版社,2004:45-54.
O241.82
A
1671-2544(2010)03-0029-02
2010-03-03
李 娟(1984— ),男,湖北广水人,北京理工大学机电学院硕士研究生。

