一类矩阵的秩恒等式

黄 弘,熊一能

(孝感学院数学与统计学院,湖北孝感432000)

一类矩阵的秩恒等式

黄 弘,熊一能

(孝感学院数学与统计学院,湖北孝感432000)

利用计算不为0的特征值的个数来计算矩阵的秩,得到一类矩阵秩的几个矩阵秩恒等式,并给出它们的应用。

矩阵秩;Sylvester公式;Frobenius公式

1 介绍

设Fm×n为数域F上所有m×n阶矩阵的集合,rankA为A∈Fm×n的秩,E为单位矩阵,f(A)为A的多项式。当A∈Fm×n,正整数m≥2时,如果Am=A,且Ak≠A(k=2,3,…,m-1),称A为m-幂等矩阵;如果Am=A,且Ak≠E(k=1,2,…,m-1),称A为m-对合矩阵。

矩阵的秩是线性代数中一个基本而深刻的概念。关于矩阵的秩,有一系列的基本不等式,其中Sylvester不等式与Frobenius不等式占有重要的地位。下面是著名的Sylvester与Frobenius不等式:

Sylvester不等式 设A∈Fm×n,B∈Fn×1,C∈Fl×s,则

rankA+rankB≤rank(AB)+n

Frbenius不等式 rank(AB)+rank(BC)≤rank(AB C)+rank(B)。

关于矩阵多项式的秩的恒等式,它已成为众多研究者的研究课题,获得了不少好的结果[3-4]。2008年,胡付高等在文献[4]中讨论了矩阵的秩Frobenius公式等号成立的条件,并给出了下列结论:

命题1[4]设A∈Fn×n,f(x),g(x),h(x)∈F[x],(f(x),h(x))=1,则

rank[f(A)g(A)]+rank[g(A)h(A)]=rank[f(A)g(A)h(A)]+rank[g(A)]。

注意到命题1取g(A)=E,便得到文献[3]矩阵的秩Sylvester公式等号成立的条件。

命题2[3]设f(x),g(x)∈F[x],(f(x),g(x))=1,A∈Fn×n,则

rank(f(A))+rank(g(A))=

rank(f(A)g(A))+n。

命题3[3]设A∈Fn×n,f(x),g(x)是数域F上的多项式,(f(x),g(x))=1,则f(A)g(A)=O当且仅当rank[f(A)]+rank[g(A)]=n。

注意这些结论都是分块矩阵的初等变换方法得到的。

对A∈Fn×n,若存在可逆矩阵P,使得PA P-1为上三角矩阵Λh,本文称Λh为A的三角矩阵,记作ΛA。显然ΛA的对角线上的元素为A的特征值。记G是一个Fn×n中的具有交换性的矩阵集,即任意A,B∈G,AB=BA;令

M={A∈G|ΛA的为0特征值所在行的行向量全为0}。

显然M中任意矩阵A的秩等于其不为0的特征值的个数,也等于ΛA不为0的行向量的个数。例如:设A∈Fn×n,A2=E,则A+E,A-E∈M。

本文利用求矩阵不为0的特征值的个数,研究M中矩阵的秩Frobenius公式和Sylvester公式等号成立的条件,得到几个矩阵秩恒等式,并给出它们的应用。

2 引理

引理1[1]设A,B,C∈Fn×n,且两两互换(即AB=BA,AC=CA,BC=CB),则A,B,C存在有一个公共特征向量。

引理2 设A,B,C是复数域上n级矩阵,若它们两两互换,则存在可逆矩阵P,使得P-1A P,P-1B P,P-1CP均为上三角矩阵。

证明 对A,B,C的级数n用数学归纳法。

1)当n=1时,结论显然成立。

2)设A,B,C均为n-1级方阵时,结论成立。当A,B,C均为n级方阵时,设σ,τ,θ是复数域上n维线性空间V的两个线性变换σ,τ,θ在基α1,α2,…αn,下的矩阵,存在公共特征向量β1,使得σ β1=λ1β1,τ β1=μ1β1,θ β1=l1β1,λ1,μ1,l1是复数,把β1扩充为V的基β1,β2,…,βn,则A,B,C在基β1,β2,…,βn下的矩阵分别为其中A1,B1,C1为n-1级方阵。设(β1,β2,…,βn)=(α1,α2,…,αn)P1,则

因为A,B,C两两互换,所以A1,B1,C1两两互换,由归纳假设存在n-1级方阵P2使得

3 主要结果

定理1 设A,B∈M,rank(A+B)=n,则

rankA+rankB=n+rankAB。

证明 不妨设F为复数域,设A,B的特征值为α1,α2,…,αn和β1,β2,…,βn。因AB=BA,由引理2(取C为单位矩阵),存在矩阵P使得

于是AB的特征值为λ1μ1,λ2μ2,…,λnμn。

因rank(A+B)=n,故λj,μj不能同时为0,1≤j≤n。

定义|{x|x∈Q}|为集合Q中元素x的个数,则rankAB=|{λjμj|λjμj≠0,1≤j≤n}|。

rankA+rankB=|{λj|λj≠0,1≤j≤n}|+|{μj|μj≠0,1≤j≤n}|=|{(λj,μj)|λi≠0且μj=0,1≤j≤n}|+|{(λj,μj)|λi≠0且μj≠0,1≤j≤n}|+|{(λj,μj)|λi=0且μj≠0,1≤j≤n}|+|{(λj,μj|λi≠0且μj≠0,1≤j≤n}|=n+|{(αj,βij)|αi≠0且βij≠0,1≤j≤n}|=n+rankAB

此定理的逆命题不成立。

特别地,有

推论1 设A,B∈M,rank(A+B)=n,则AB=BA+O当且仅当rankA+rankB=n。

定理2 设A,B,C∈M,rank(A+C)=n,则rankAB+rankBC=rankAB C+rankB。

证明 不妨设F为复数域,设A,B,C的特征值为λ1,λ2,…,λn;μ1,μ2,…,μn和l1,l2,…,ln。因A,B,C两两互换,由引理2存在矩阵P使得

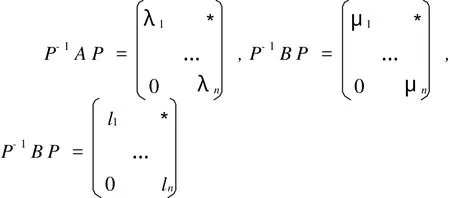
于是AB,BC,AB C的特征值为λ1μ1,λ2μ2,…,λnμn;μ1l1,μ2l2,…,μnln;λ1μ1l1,λ2μ2l2,…,λnμnln。由定理1的证明知,因rank(A+C)=n,故λj,l1不能同时为0,1≤j≤n。

我们考虑当μi取不同值时,μi对rankAB+rankBC和rankAB C+rankB的贡献:

1)当μi=0,λi,l1对rankAB+rankBC和rankAB C+rankB的贡献均为0;

2)当μi≠0,λi,li对rankAB+rankBC的贡献取决于λi,li是否为0,当它们均不为0时,贡献为2,否则贡献为1(因对任意1≤i≤n,λi,li不会全为0),此时λi,li对rankAB C+rankB的贡献分别为2和1,故有:

rankAB+rankBC=rankAB C+rankB。

4 主要结果的应用

命题4 设A∈Fn×n,若A3=A,则

rankA+rank(E-A)+rank(E+A)=2n。

证明 A3=A,

A,E-A,E+A∈M

rankE=rank[(E+A)+(E-A)]

由定理1

rank(E+A)+rank(E-A)=n+rank(EA2)

同理

rankA+rank(E-A2)=rankA2+rank(EA2)=n+rank(A-A3)=n

所以

rankA+rank(E-A)+rank(E+A)=2n

下列命题均可依上述方法证明。

命题5[1]设A∈Fn×n是幂等阵(即A2=A)的充要条件为:

rankA+rank(A-E)=n。

命题6 设A∈Fn×n是对合阵(即A2=E)的充要条件为:

rank(A+E)+rank(A-E)=n。

命题7 设A∈Fn×n,m为正整数,则:

Am+1=A⇔rankA+rank(A-E)+rank(Am-1+Am-2+…+E)=2n。

充分性可由Sylvester不等式证明。

命题8 设A∈Fn×n,m为正整数,k,l为任意自然数,则

rankAl+rank(Am-E)k=n,当Am+1=A;

rank(A-E)l+rank(Am-1+Am-2+…+E)k=n,当Am=E。

[1] 北京大学数学系几何与代数研究室代数小组.高等代数[M].3版.北京:高等教育出版社,2003.

[2] Horn R A,Johnson C R.Matrix Analysis[M].New York:Academic Press,1991.

[3] 胡付高.一类矩阵多项式的秩特征[J].大学数学,2007,23(2):164-166.

[4] 胡付高,曾玉娥.一类矩阵多项式秩的恒等式与应用[J].山东大学学报:理学版,2008,43(8):51-54.

Abstract:The rank of a matrix can be obtained by calculating the number of its eigenvalues which are not 0.In this paper,by calculating the rank of a matrix,several rank identical relations of a class of matrix are obtained and some applications are given.

Key Words:rank of matrix;Sylvester formula;Frobenius formula

The Rank Identities of a Class of Matrix

Huang Hong,Xiong Yineng
(School of Mathematics and Statistics,Xiaogan University,Xiaogan,Hubei432000,China)

O151.12

A

1671-2544(2010)03-0020-03

2009-11-20

黄 弘(1969— ),男,湖北孝昌人,孝感学院数学与统计学院讲师,硕士。

(责任编辑:周 游)