α−幂过程维修模型下的最优更换策略

陈建勇，应巨林，邹良影，闫长远

(温州科技职业学院，温州浙江 325006)

α−幂过程维修模型下的最优更换策略

陈建勇，应巨林，邹良影，闫长远

(温州科技职业学院，温州浙江 325006)

研究一种新的α−幂过程维修模型.假设有两同型部件组成的冷贮备系统，以部件1的修理次数N为更换策略，利用更新理论，得出了平均费用率的表达式，并通过数值模拟实例得出了最优更换策略N*.

冷贮备系统；α−幂过程；更换策略

冷贮备系统是可靠性数学的主要研究对象，也是工程中运用比较多的一类系统.所谓冷贮备系统是指贮备的部件在贮备期不失效也不劣化，贮备期的长短对以后使用的工作寿命没有影响.在一般情况下，系统的失效修理并不能修复如新，修理后的寿命逐渐递减并最终不能工作，这样的系统被称为退化系统.常见的退化系统被描述为单调几何过程.Braun等[1]提出了一种全新的单调过程——α−幂过程，并且发现α−幂过程具有与几何过程相类似的性质.许多学者利用α−幂过程理论研究了退化可修系统的最优更换策略[2-3].本文将采用α−幂过程理论对冷贮备系统进行讨论，并以部件1的修理次数N作为更换策略.

1 α−幂过程的定义和有关定理

2 模型假设

假定1 开始时，系统的两部件都是新的，并且部件1首先工作，部件2冷贮备.

假定2 当系统两个部件均正常时，一个工作，另一个冷贮备.当系统部件失效时，修理工立即进行维修，同时，冷贮备部件立即开始工作，修好后的部件要么进入工作状态，要么进入贮备状态.若一个失效部件未修好时，另一个部件也失效，则它必须处于待修状态，这时系统失效.

假定3 系统任何部件均不能修复如新，设和分别表示部件i第n−1次修理后的剩余寿命和第n次修理时间，其分布函数分别为F(na t)和G(nb t)，其中a>0，b<0，这样，{,n= 1,2,L}是α−幂递减过程，相应的{Y(i),n= 1,2,L} 是α−幂递增过程，且设=λ，=μ，由定理1得：

假定5 系统中的部件更换时，用新的同类型部件进行更换，且更换时间忽略不计.

假定6 冷贮备中的部件不产生工作报酬，待修的部件不产生维修费用.

假定7 系统中的每个部件在单位时间内的维修费用为cr，单位时间内的工作报酬为cw，更换一个费用为c.

3 策略N下的平均费用率表达式

当部件1的修理次数达到N时，部件2必然已经修理了N−1次，且要么处于工作状态，要么处于待修状态，前者继续工作直到第N+1次失效发生，而后者不需要再进行修理.令W1表示部件1首次更换时间，则{Wn,n≥ 2}为系统第n−1次与第n次更换时间间隔，则{Wn,n= 1,2,L}形成了一更新过程.令Un表示更换时间间隔Wn内的费用，则{Un,n= 1,2,L}就是酬金过程，因此{(Wn,Un)}形成一个带酬更新过程.

设C(N)为系统在策略N下经长期运行单位时间内的期望损失，由酬金过程的更新定理[4-5]知：

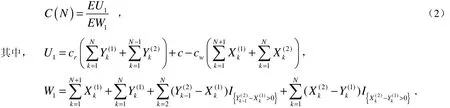
定理2 如果X,Y是两个非负独立的随机变量，它们的分布函数为F(x),G(x)，则

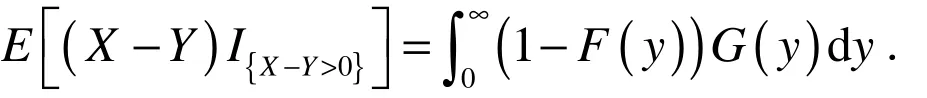
证明：因为X,Y是两个非负独立的随机变量，所以有：

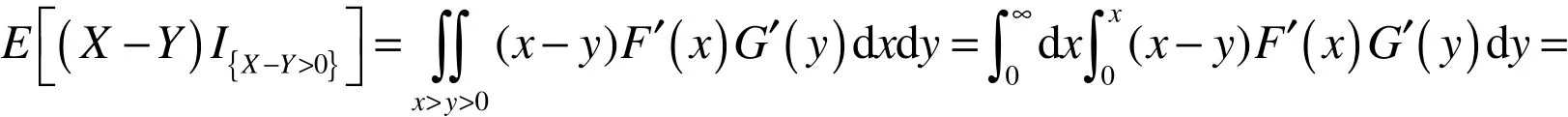
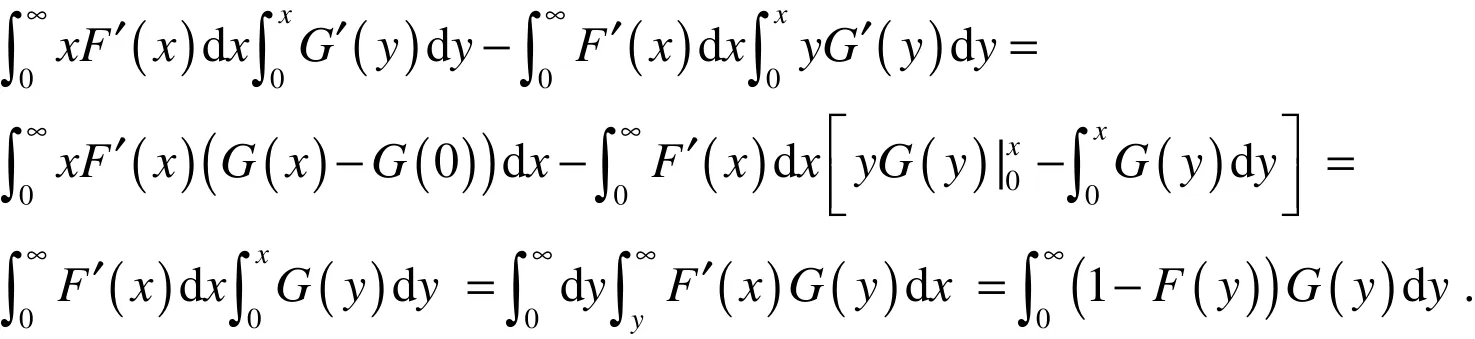
下面利用数值实例，对（2）式进行最小化，求最优更换策略N∗.

4 数值模拟实例

如果和都服从指数分布：

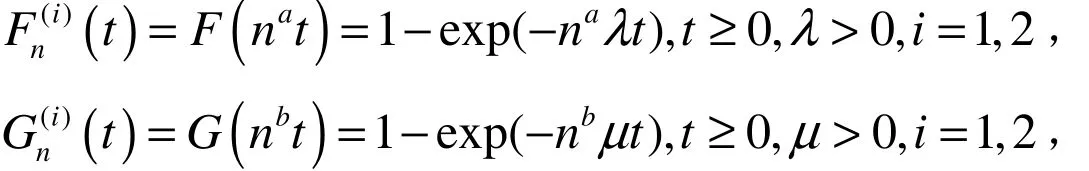
式，利用Matlab软件，得到C(N)随N变化的数据及图形.见表1和图1.

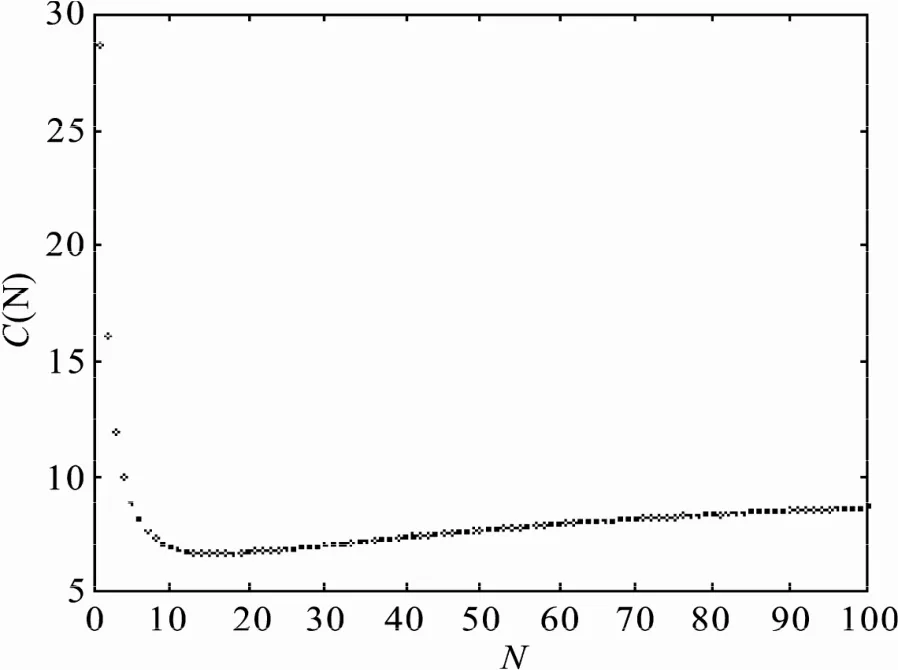
图1 C(N)随N的变化曲线Fig 1 Curve of C(N) by N

由表1和图1知，C(1 6 )= 6.624是平均费用率的最小值，即当部件1修理次数达到16并且发生第17次失效时就应该更换了.

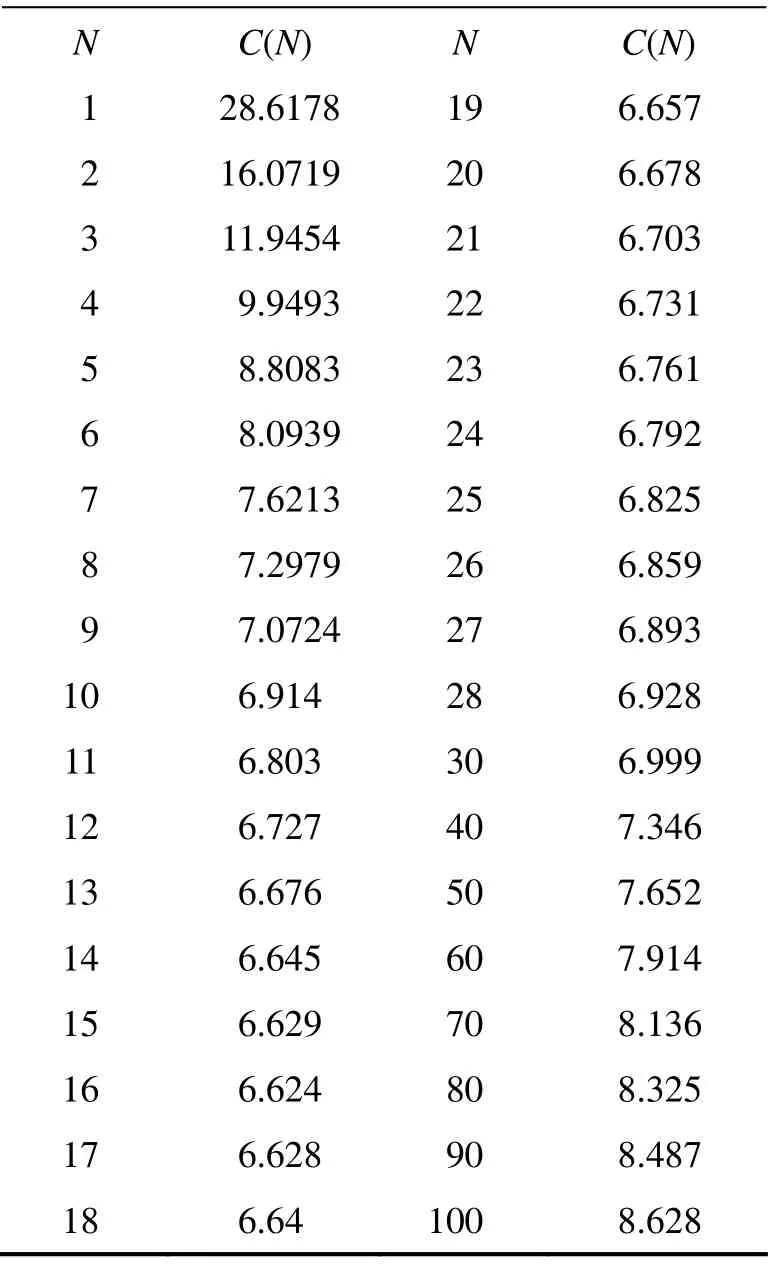
表1 C(N)随N变化的数据表Table 1 Date Sheet of C(N) by N

[1]Braun W J, Li W, Zhao Y Q. Properties of geometric and related process [J]. Naval Research Logistic, 2005, 52: 607-616.

[2]周玉霞. 退化系统的α−幂过程维修模型的最优更换策略的单调性[J]. 四川大学学报: 自然科学版, 2007, 44(2): 221-224.

[3]唐亚勇, 刘亚萍.α−退化系统的幂过程维修模型[J]. 四川大学学报: 自然科学版, 2007, 44(3): 503-507.

[4]龚光鲁, 钱敏前. 应用随机过程教程[M]. 北京: 清华大学出版社, 2004: 56-57.

[5]曹晋华, 程侃. 可靠性数学引论[M]. 北京: 高等教育出版社, 2006: 100-105.

Research on Optimum Replacement Policy ofα−Power Process Maintenance Model

CHEN Jianyong, YING Julin, ZOU Liangying, YAN Changyuan
(Wenzhou Vocational College of Science and Technology, Wenzhou, China 325006)

A newα−power process maintenance model was studied. Based on the assumption of a cold standby system consisting of two identical components, the expression of average cost rate could be achieved by takingN, the failure number of the component 1, as replacement policy and using renewal theory. Then, the optimum replacement policyN*could be obtained through numerical simulation example.

Cold Standby System;α−Power Process; Replacement Policy

(编辑：王一芳)

O151.23

A

1674-3563(2010)06-0007-04

10.3875/j.issn.1674-3563.2010.06.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2010-05-11

陈建勇(1984- )，男，浙江温州人，助教，硕士，研究方向：系统可靠性