从MPEG-2到H.264的视频格式转换算法

陈荣荣

（肇庆学院 电子信息与机电工程学院，广东 肇庆 526061）

0 引 言

在MPEG-1、MPEG-2、H.263等视频编码方法中，普遍采用离散余弦变换（Discrete cosine transform，DCT）编码[1]；而最新的国际视频编码标准H.264，又被称为MPEG4-AVC，则采用了整数变换（Integer transform,IT）编码[2].由于MPEG-4具有压缩率高，但画面和声音质量却没有太大损失的优点，它在现在的视频编码领域占有重要地位；因此，研究如何把MPEG-1、MPEG-2、H.263等格式的视频转换为MPEG-4格式的视频具有重要意义.格式转换的核心步骤是从离散余弦变换参数到整数变换参数的转化，简称为DCT-to-IT变换（DCT-to-IT conversion，DIC）.文献[3]2－3对此过程作了介绍，但缺乏对此算法的具体推导.本文中，笔者从离散余弦变换和整数变换的理论基础出发，详细推导了DCT-to-IT变换的过程，对文献[3]2－3中提出的方法作进一步说明和修正，提高了执行效率，并提供了仿真结果作为参考依据.

1 变换方法的理论基础

1.1 离散余弦变换（DCT）

编码过程中，DCT的变换与逆变换公式分别如式(1)和(2)所示：

其中：u＝0时，Cu＝1/；u＞0时，Cu＝1；v＝0时，Cv＝1/；v＞0时，Cv＝1.

如果将离散余弦变换的量化矩阵表示为Q(u,v)，则量化与反量化的过程分别以如下式(3)和(4)表示：

其中round[.]表示取与该分数值最接近的整数.亮度和色度量化矩阵的值QL和QC可在文献[4]中查得.

量化因子qJPEG用于限制量化矩阵Q(u,v)的值，范围在1%～100%.在式(3)和(4)中，量化矩阵的各元素都和压缩因子α相乘，α的定义如下：

1.2 整数变换（IT）

MPEG-1、MPEG-2、H.263等采用的是8×8 DCT模块；而H.264采用的则是4×4 IT模块[5]，它的公式表示为

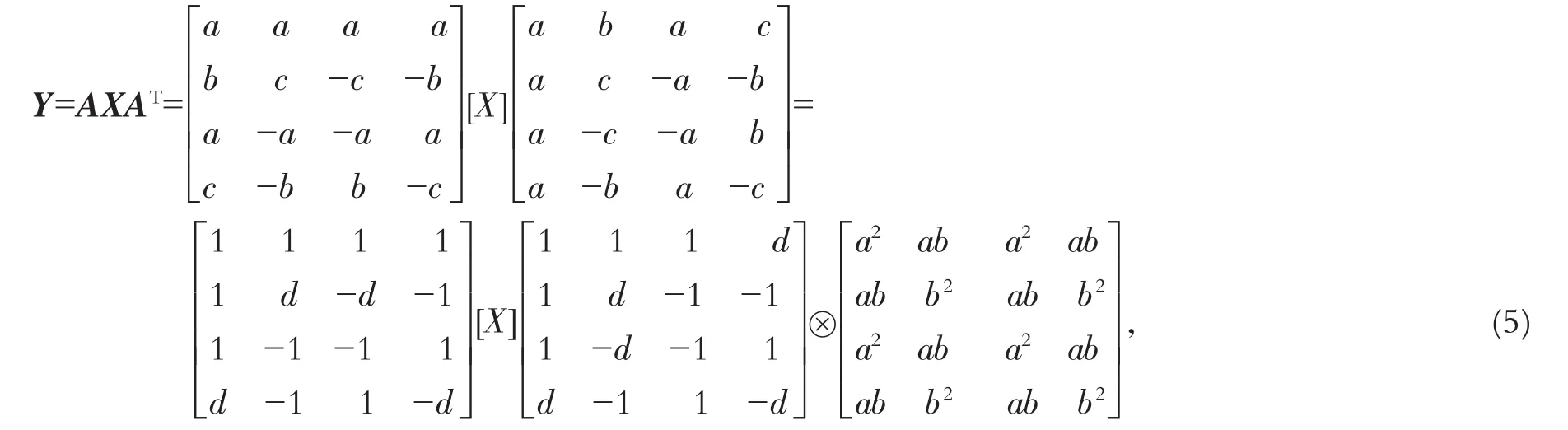
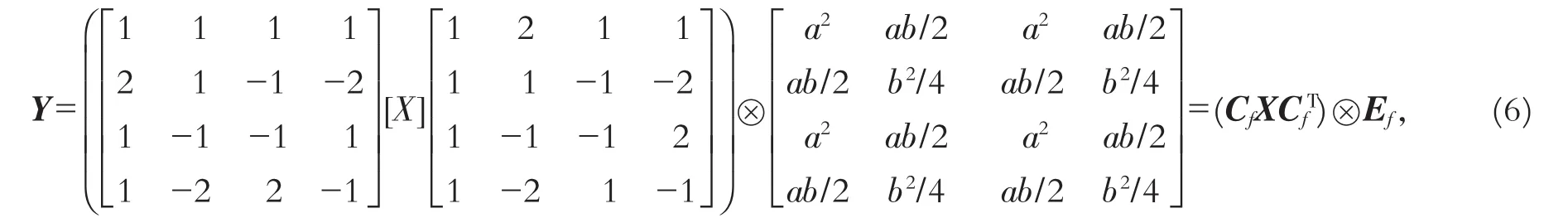
其中：

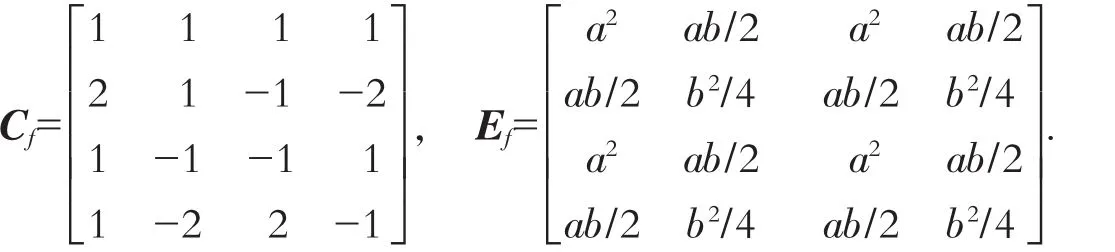
整数变换的逆变换（IIT）的定义如下：

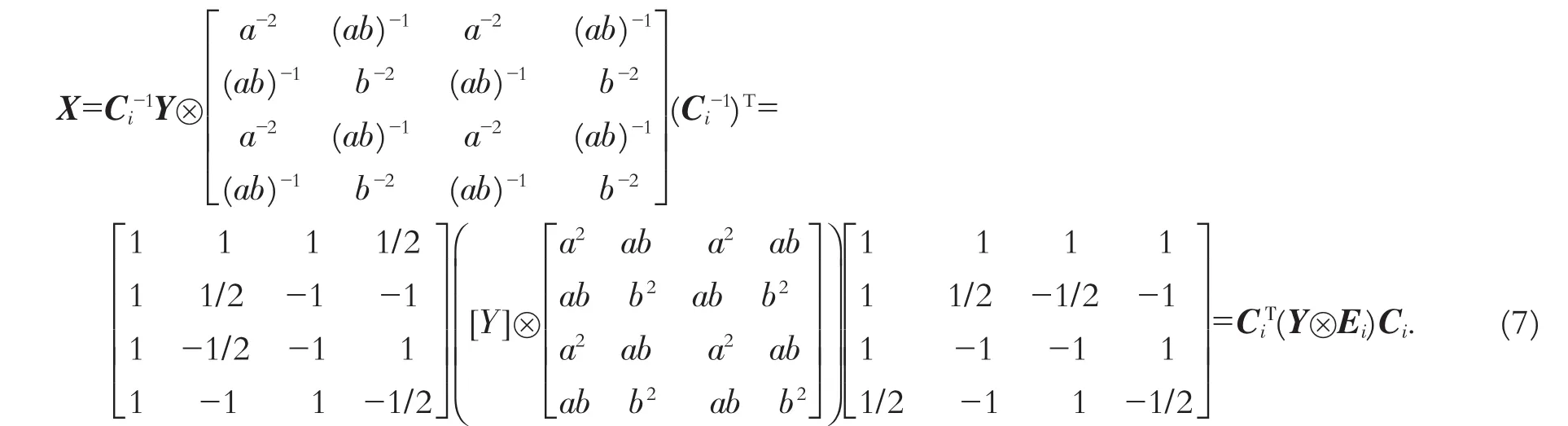
其中

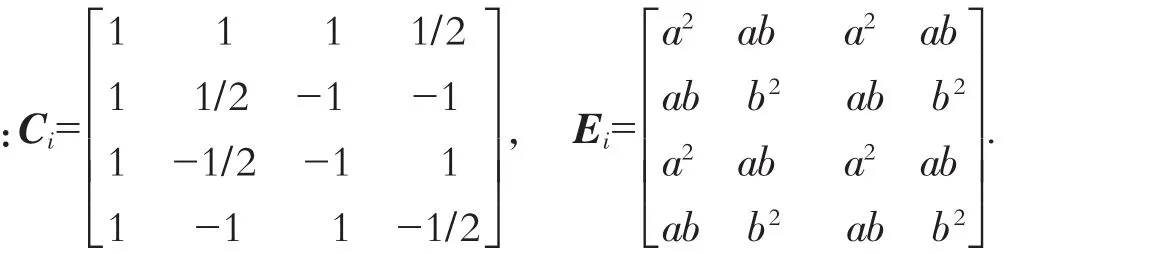
整数变换中量化与反量化的过程分别由(8)和(9)实现，Yij为矩阵Y在i，j处的值.

H.264使用了分级量化器，支持52个量化步长，用量化参数来索引量化步长，量化步长用Qstep表示，量化参数用QP表示.QP每增加1，Qstep就增加12.25%；QP每增加6，Qstep就增加1倍.其中QP＝0时，Qstep＝0.625；QP＝51时，Qstep＝224.

1.3 离散余弦变换到整数变换的转换

图1示意了像数域的离散余弦变换到整数变换的转换过程，输入8×8的离散余弦变换参数模块（X），并以经过逆离散余弦变换后新的8×8模块（x）覆盖原来的模块.新的8×8模块被均匀地分为4个4×4模块（x1，x2，x3，x4），每个4×4模块都经过相应的整数变换成为新的4×4参数模块，并重新组合为新的8×8模块，这个过程会在视频的所有模块中重复.

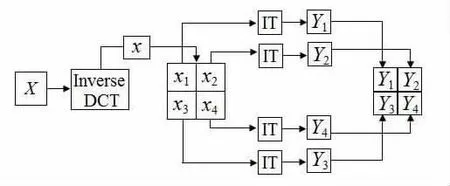
图1 像数域的离散余弦变换到整数变换的转换过程

由于不需要进行完整的解码和再编码，在变换域中完成DCT到IT的转换比在像数域中完成该转换更有效[6]498－500，因此，我们需要寻找一种在变换域中完成DCT到IT的转换方法.图2示意了一种假设在变换域中完成的DCT到IT的转换过程，将这个变换简称为DIC（DCT-to-IT conversion）.它可以把一个输入为MPEG-2格式视频的DCT参数（X）转换为输出为AVC格式视频的IT参数（Y）.假设DIC的过程由一个8×8的核心矩阵S表示[3]2：

图2 DCT到IT的转换过程

S矩阵的推导过程如下：

x被均匀划分为4个小矩阵x1，x2，x3，x4，由式(6)可知其整数变换过程可以分别表示为

其中，x是X的IDCT.令T8为DCT的核心变换矩阵，那么有x＝T8TXT8.

由上面的分析可以推导出

在文献[3]2－3中，DIC的转换过程仅由式(10)表示.由以上推导过程可发现文献[3]2－3没有把缩放因子Ef考虑在内，对结果可能造成一定误差，因此，笔者推导的DIC过程由式(14)定义.

如果保留文献[3]2－3中对DIC过程的推导，则要考虑在量化过程中合并缩放因子PF(a2,ab/2,b2/4).输入矩阵X可以变换为未缩放的系数矩阵W＝，每个系数Yij的量化和缩放在一步操作中完成，公式为

其中：Yij，Zij的含义与式(8)相同；PF的值由i，j决定，为Ef位于i，j处的元素值.

反变换时的缩放因子Ei也可以合并到这个操作中，并乘以一个缩放因子常量64以避免过程中的舍入误差，则反量化和缩放的过程如下：

其中：Wij表示恢复后的系数，用来作为下一步进行反变换的输入，公式为X＝WCi.反变换后的输出值要除以64，以消除恢复过程中引入的因子常量64.正向变换和反向变换时PF的值如表1所示.

表1 正向变换和反向变换时的PF值

2 算法的仿真

图3示意了对算法的仿真过程.每帧图像都被划分为许多8×8的模块（x），经过DCT、量化（Q1）及反量化（IQ1）后，重构的参数（X）被送进2个处理系统.这2个系统都是将X映射到整数变换域，其中第1个系统经过DIC和IT的量化（Q2）、反量化（IQ2）及IIT后，重构出原图像（xS1），其中量化过程Q2分别按式(8)和(15)执行，DIC过程分别标记为DIC1和DIC2，以比较本文推导的DIC方法与文献[3]2－3推导方法的结果，重构图像分别记为xS1和xS2；第2个系统经过IDCT、IT、量化（Q2）、反量化（IQ2）及IIT完成原图像的重构（xR）.另外，还仿真了DCT和IT的过程，由这2个系统重构出的像数模块分别记为xD和xI.按文中出现的说明顺序，这4个系统分别标记为ST(ST1,ST2)、DCTIT、DCT和IT，除ST2外，其余系统的IT量化过程均按式(8)执行.比较上述4个系统重构的图像，用以判断DIC转换方法得到图像质量的优劣.

峰值信噪比δ经常用作图像压缩等领域中信号重建质量的测量方法，它常简单地通过均方差S定义.2个m×n单色图像I和K，如果一个为另外一个的噪声近似，那么其均方差定义为

峰值信噪比定义为

其中，Imax是表示图像点颜色的最大数值.如果每个采样点用8位表示，那么就是255.

每点有R，G，B 3个值的彩色图像，其峰值信噪比的定义类似，只是均方差是所有方差之和除以图像尺寸再除以3，如式(19)所示.

其中：IR，IG，IB，KR，KG和KB分别表示原始图像和解压缩后图像的R，G，B这3层的值.δ愈高愈好，即S越小越好.

图3 算法的仿真过程

3 结果分析与比较

根据上面的分析可知，在DCT中，取α＝99可得到最大的峰值信噪比δ；在IT中，取Qstep＝0.625可得到最大的δ因此在仿真过程中取这2个值作为量化的参数.应用Matlab软件仿真了离散余弦变换（DCT整数变换（IT）、在像数域（DCTIT）和转换域（DIC）进行的离散余弦变换参数到整数变换参数的转换过程，并分别选取了以人物、风景、汽车、建筑、动物为主要背景，在白天、黑夜等不同时间拍摄的JPG格式图片，比较具有代表性.比较图片经过上述4个系统之后的δ值，特别对经过系统1和系统2之后的δ值进行比较.同时，在相同的运行环境下，对同一图片的DIC1和DIC2过程分别运行10次，计算这10次的平均执行时间，以评估这2种算法的效率.比较结果如表2所示.

表2 不同编码方式的δ值结果比较

由以上10组图片的比较结果可以看出，δIT＞δDCT＞δDIC＞δdctit.由δDIC和δdctit的比较结果可见，在转换域进行的参数变换DIC优于在像数域进行的参数变换，与文献[6]498－500提出的结论相符合.在相同的运行环境下，运用式(8)和(15)这2种量化方法推导的DIC过程所得的峰值信噪比相等.由DIC1和DIC2的程序执行时间比较可见，tDIC2＞tDIC1.这是由于在按式(15)进行量化的DIC2中，程序每循环1次都需要根据该像数点的位置(i,j)判断PF的值，而这个判断过程本身也是1次循环，多重循环的嵌套使程序的执行效率较低，耗时较长.10组图片的DIC1执行时间皆比DIC2执行时间短，且时间缩短较为明显，由此可总结出笔者推导的DIC公式(14)比文献[3]2－3中推导的公式(10)具有更高的效率.

4 结论

本文中，笔者讨论了一种在变换域中完整地将DCT参数转换为IT参数的方法，并应用Matlab程序仿真了离散余弦变换、整数变换、在像数域和转换域进行的离散余弦变换参数到整数变换参数的转换方法，即从MPEG-2到H.264/MPEG4-AVC的参数转换方法.在对转换方法进行推导的同时，对原有方法加以完善补充，提高了程序的效率，节省了执行时间.最后选取了10组内容、背景、尺寸不同的图片，对采用不同方法编码、解码后的图像质量进行了比较，验证了在转换域进行MPEG-2到AVC/MPEG-4参数转换的可行性，为简化和改进视频压缩方法提供了依据.

[1] International Organization for Standardation,International Electrotechnical Commission.ISO/IEC 13818-2,Information technologygeneric coding of moving pictures and associated audio information:Video[S].2nd ed.2000.

[2] WEIGAND T,SULLIVAN G J,BJNTEGAARD G,et al.Overview of the H.264/AVC video coding standard[J].IEEE Trans Circuits Syst Video Technol.2003,13(7):560-576.

[3] XIN Jun,ANTHONY V,SUN Hufang.Converting DCT coefficients to H.264/AVC Transform Coefficients[C]//Mitsubishi Electric Research Laboratories.2004:6.

[4] GHANBARI M.Video Coding:A Introduction to Standard Codecs[M]//IEEE Telecommunications Series 42.1999:52-54.

[5] 毕厚杰.新一代视频压缩编码标准——H.264/AVC[M].2版.北京:人民邮电出版社,2005:111-117.

[6] KEESMAN G,HELLINGHUIZEN R,HOEKSEMA F,et al.Transcoding of MPEG bitstreams[J].Signal Processing:Image Communication,1996(8):481-500.