非线性光纤光栅双稳特性研究

田剑锋 阎元红

（太原师范学院物理系,山西太原 030031）

非线性光纤光栅双稳特性研究

田剑锋 阎元红

（太原师范学院物理系,山西太原 030031）

从非线性耦合模理论出发,对非线性光纤光栅双稳特性作了理论研究,并采用数值模拟的方法研究了非线性布喇格光栅双稳态对光栅内部参数的依赖性.结果表明:非线性光纤光栅双稳特性对光栅本身的耦合系数和光栅长度具有一定的依赖性,合理选择光栅的长度和耦合系数可以改善双稳的开关阈值、环的宽度以及开关对比度.

非线性光纤光栅;光学双稳;耦合系数;光栅长度

0 引言

光纤光栅以其独特的非线性特性在全光限制器、光学开关、孤子通信等领域展现了巨大的应用潜力[1～3].随着科学技术及工艺水平的提高,光纤光栅在长度和折射率调制深度上都可在几个数量级之间变化.因此,即使在非线性折射率系数很低的普通光纤中刻上光栅,无需很高的入射光功率也能引发明显的非线性效应.在“光子禁带”（PBG）内,由于非线性折射率、内部能量、入射光与布喇格谐振频率间的失谐量构成的正反馈环导致光子禁带随入射能量的变化而移动,最终呈现双稳开关效应[4～8].本文从耦合模理论出发,利用数值模拟的方法,对非线性布喇格光栅双稳态对光栅内部参数依赖性进行了研究.研究结果表明:非线性光纤光栅双稳特性对光栅本身的耦合系数和光栅长度具有一定的依赖性,合理选择光栅长度和耦合系数可以改善双稳的开关阈值、环的宽度以及开关对比度.

1 理论模型

考虑一维光纤光栅,其轴向沿z方向,其折射率分布为:

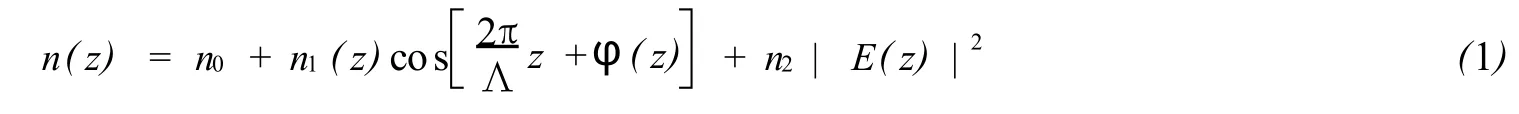
式中E（z）为光栅内部电场振幅,Λ为布拉格周期,φ（z）为光栅中的相移,n0,n1（z）以及n2分别为光栅平均折射率、折射率周期变化振幅以及非线性克尔系数.光栅内传播的电场可以写作:

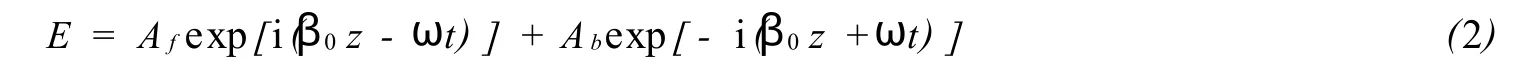
式中ω为光载波的中心角频率,t为时间,β0=π/Λ为布拉格波数,Af和A b分别是光栅中前向和后向波的振幅慢变包络函数.在本文的计算中,只考虑入射波为连续波或准连续波的情况.把（2）式代入波动方程并结合（1）式,忽略光纤的损耗及材料色散（假定NLBG的介质为无抽运的掺铒光纤,虽然该材料在1.55μm窗口有较大的损耗和色散,由于计算中所选光纤的长度为cm量级,因此其损耗及色散可以忽略）,并假设材料非线性响应速度特别快,以及载波波长接近光栅的布拉格波长,就可得到如下非线性耦合模方程[5]:

式中vg为光在光栅中传播的群速度,δ为失谐量,Γ为非线性系数,k为耦合系数.δ,Γ以及k分别表示为:

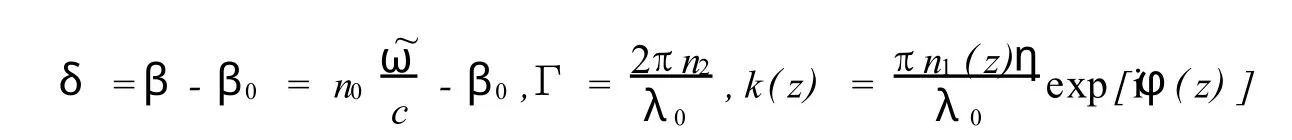
式中c为真空中的光速,λ0=2n0Λ为布拉格波长,η为限制因子.对于均匀非线性光纤光栅,k可表示为常数即:

式中L为光栅的总长度,k0为光栅中心处的耦合系数.

对于非线性均匀光纤光栅,其布拉格波数β0将随轴向不变,可表示为:

式中为平均布拉格波数.

慢变振幅在边界处满足下列边界条件:

式中Ai,Ar及A t分别为入射波、反射波及透射波的慢变振幅.

在（3）,（4）式中,令对时间的偏导为0,得到稳态时慢变振幅沿轴向的变化方程.结合边界条件（5）,（6）,借助四阶龙格-库塔法可进行数值求解,从而可对其双稳特性进行研究.

2 结果与讨论

在计算过程中,所用的数据为:λ0=1.55μm,n0=1.46,n2=6.9 ×10-15m2/W,η=0.8,为了方便讨论,以下输入光强Ii、输出光强It分别对Ic进行归一化,其中Ic=4λ0/（3πn2L）为入射临界光强.

2.1 NLBG双稳态对光栅耦合系数的依赖性

图1给出了k取不同值时NLBG稳态输入-输出曲线.从图1中可以明显发现:入射光波长和光栅长度一定时,NLBG输出双稳态对耦合系数的依赖关系.当k=2.0 cm-1时,入射光接近透射态,光栅内部反馈较弱不足以产生双稳现象;当k增大到2.5 cm-1时,光栅内部反馈增强,双稳现象发生;当k继续增大时,双稳环宽度明显增大,而且还可产生多个双稳区域.以上结果表明,在实际应用中通过合理选择k可对光栅的双稳态性能进行进一步的优化.

图1k取不同值时NLBG稳态输入-输出曲线

Fig.1kNLBG steady state for different values of inp t-output curve

2.2 NLBG双稳态对光栅长度的依赖性

图2给出了光栅长度分别取不同值时,布拉格光栅的稳态输入-输出曲线,图中曲线a,曲线b,曲线c分别对应光栅长度L取1.5 cm,2.0 cm,2.5 cm,从图中可以看出:当光栅的耦合系数确定以后,光栅长度对双稳的开关阈值、环的宽度、开关对比度以及双稳环上支透过率都有较大的影响.当L较小时将没有双稳现象产生;当L较大时将出现双稳,并且随着L的增大,双稳环的宽度将逐渐增加,开启阈值逐渐减小,开关对比度增大;当L增大到一定时,将出现两个双稳区域新增加的双稳区位于临界光强附近.

总之,非线性均匀光纤光栅双稳态性能对其自身的耦合系数k和光栅长度L具有一定的依赖性:当k值太小,输出无双稳现象;随着k值的增大,开始出现双稳现象,并且双稳环宽度也逐渐增大;当k增大到一定时,将出现两个双稳区域;当光栅的耦合系数确定以后,光栅长度对双稳的开关阈值、环的宽度、开关对比度等都有较大的影响.因此,在实际应用中可以通过合理选择耦合系数和光栅长度从而对非线性光纤光栅双稳态性能进行优化.

图2 L取不同值时NLBG稳态输入-输出曲线Fig.2 L NLBG steady state for different values of input-output curve

3 结论

利用耦合模理论数值研究了光纤长度L和耦合模系数k对非线性光纤光栅双稳特性的影响.结果表明:当k值太小,输出无双稳现象;随着k值的增大,开始出现双稳现象,并且双稳环宽度也逐渐增大;当k增大到一定时,将出现两个双稳区域;当光栅的耦合系数确定以后,光栅长度对双稳的开关阈值、环的宽度、开关对比度等都有较大的影响.因此,在实际应用中,需合理选择光栅的长度和耦合系数.

[1] Eggleton B J,Lenz G,Litchinitser N M.Optical pulse comp ression schemes that use nonlinear Bragg gratings[J].Fiber and Integrated Opt.,2000,19（4）:383-421

[2] Radic S,George N,Agrawal G P.Analysisof nonuniform nonlinear distributed feedback structures:Generalized transfer matrix method[J].IEEEJ.Quantum Electron.,1995,31（7）:1 326-1 336

[3] Radic S,George N,Agrawal G P.Optical switching inλ/4-shifted nonlinear periodic structures[J].Opt.Lett.,1994,19（21）:1 789-1 791

[4] Radic S,George N,Agrawal G P.Theory of low-threshold optical switching in nonlinear,phase-shifted,periodic structures[J].Opt.Soc.Am.B,1995,12（4）:671-680

[5] Jia X H,Wu ZM,Xia GQ.Analysisof bistable steady characteristics and dynamic stability of linearly tapered nonlinear bragg gratings[J].Opt.Exp ress,2004,12（13）:2 945-2 953

[6] 田剑锋,吴正茂,夏光琼.非线性布拉格光栅双稳特性的理论研究[J].物理学报,2007,56（4）:2 256-2 260

[7] 田剑锋,吴正茂,夏光琼.啁啾的引入对线性负切趾型布拉格光栅双稳特性的影响[J].物理学报,2006,55（12）:6 419-6 423

[8] 陈建军,夏光琼,田剑锋,等.一种提高λ/4相移光纤光栅开关性能的方法[J].中国激光,2007,34（9）:1 250-1 254

Investigation on the Characteristics of Fiber Gratings Optical Bistable Switching

Tian Jianfeng Yan Yuanhong
（Department of Physics,Taiyuan No rmal University,Taiyuan 030031,China）

Based on the coup led mode theo ry,the bistability performance of nonlinear bragg gratings is analyzed theo retically,and the dependence of the bistability on the gratings inner parameters is investigated numerically.The results show that,the bistability performance of nonlinear bragg gratings dependson its coup le coefficient and grating length.the sw itching threshold,the central w idth and sw itch contrast could be imp roved through choosing reasonable coup le coefficient and grating length.

nonlinear fiber gratings;op tical bistability;coup le coefficient;grating length

【责任编辑:王映苗】

1672-2027（2010）02-0074-03

O 437;TN 253

A

2010-03-19

田剑锋（1974-）,男,山西大同人,硕士,太原师范学院物理系讲师,主要从事光纤通信方面研究工作.