广义周期时变系统的二次稳定性分析

吕明珠,刘世勋

(1.辽宁广播电视大学装备技术学院,辽宁沈阳 110034;

2.中国产品质量认证中心(沈阳)北方实验室有限公司,辽宁沈阳 110141)

广义周期时变系统的二次稳定性分析

吕明珠1,刘世勋2

(1.辽宁广播电视大学装备技术学院,辽宁沈阳 110034;

2.中国产品质量认证中心(沈阳)北方实验室有限公司,辽宁沈阳 110141)

研究了广义周期时变系统的二次稳定性问题·通过建立一个Riccati方程,给出了系统在输出反馈下二次稳定的充要条件·

广义周期系统;二次稳定性;Riccati方程

1 周期系统稳定研究概述

稳定性是控制系统的一个重要特征,为此许多学者研究了系统镇定的方法·目前对于稳定性研究主要采用的是Lyapunov方法,即由一个Lyapunov函数出发,得到一个Lyapunov方程,将系统的稳定性问题转化为这个Lyapunov方程的数值解的存在性问题·Lewis第一个给出了研究广义定常系统的Lyapunov方程[1],接着Takaba等把这一结果进一步推广,使其形式更接近于正常系统的Lyapunov方程[2]·近30年来,随着周期系统在实际中的广泛应用,很多学者开始研究周期系统的稳定性问题·Bolzern等建立了正常周期Lyapunov方程,并讨论了周期系统的稳定性[3]· Bittanti又建立了周期Lyapunov不等式和Riccati方程,并给出了正常周期系统稳定的充要条件[4]·随着研究的不断深入,针对广义周期时变系统的稳定性研究已成为必然的发展趋势·广义周期时变系统是一类重要的广义时变系统,由于它自身具有周期性,因此对它的研究既广泛又方便·因此,近几年来广义周期时变系统取得的成果不断·苏晓明采用Lyapunov方法,得到了广义周期系统在状态反馈控制作用下的稳定性的判定条件,即二次稳定性问题[5]·但由于在有些情况下,系统的状态难以获得或得到的代价太高,所以状态反馈具有一定的局限性·

本文利用Lyapunov方法研究系统在输出反馈控制作用下的二次稳定性问题·因为在通常情况下系统的输出是可以直接测量的,所以可以很方便地用来构造控制器·通过建立一个Riccati方程,给出了系统二次稳定的判定条件·

2 二次稳定性分析

式中,x(t)∈Rn是系统的状态变量,u(t)∈Rm是系统的控制输入,A(t)∈Rn×n,B(t)∈Rn×m, C(t)∈Rr×n是解析的函数矩阵,rankE=q＜n,且A(t+T)=A(t),B(t+T)=B(t),C(t+ T)=C(t)·

定义1 对于系统(1),如果存在常数s,使得det(sE-A(t))≠0(∀t),则称系统(1)是一致正则的·

由定义1知,系统(1)的一致正则与Campbell意义下的解析可解性是等价的·将系统(1)进行如下分解:设

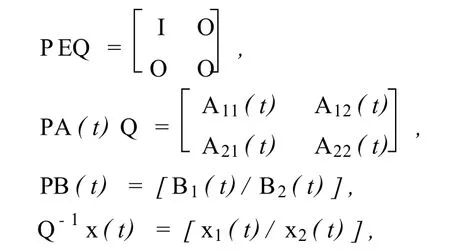
则系统(1)受限等价于

显然,系统(1)无脉冲的充分必要条件为A22(t)是可逆的,此时

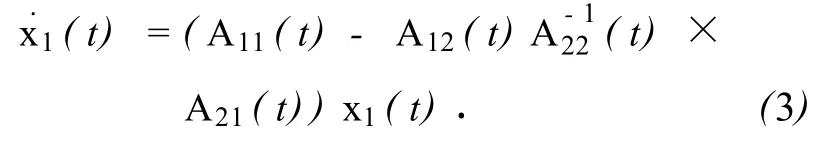
定义2 系统(2)被称为强渐近稳定的,如果系统(1)无脉冲并且是渐近稳定的·

由于系统的稳定性只与“广义状态”Ex有关,因此可以定义

引理[5]假设系统(1)是一致正则的,则系统(1)是强渐近稳定的充分必要条件为Lyapunov方程(4)有正定对称解V(t),满足

由引理可以得到系统(1)稳定的判定条件·下面进一步研究系统二次稳定的判定条件·为此,首先给出二次稳定性的定义·

定义3 对于系统(1),如果存在输出反馈

是强渐近稳定的,则称系统(1)是二次稳定的·

下面,引入记号Gi表示线性空间ImCT(t)的正交投影:

式中,C+(t)为矩阵C(t)的Moore-Penrose广义逆·

接下来,建立Riccati方程·针对系统(1)及Lyapunov方程(4),可定义如下Riccati方程:

式中,R(t)＞0,W(t)＞0·

利用Riccati方程(5),有如下结论:

定理 设系统(1)是一致正则的且无脉冲,则系统(1)是二次稳定的充分必要条件为存在矩阵W(t)＞0,使得Riccati方程(5)有半正定解V(t),满足

显然,上式为闭环系统的Lyapunov方程,由引理知,系统是稳定的·

必要性·假设系统(1)是稳定的,即存在输出反馈矩阵F(t),使得闭环系统

3 总 结

本文用一个新型的Lyapunov方程和Riccati方程处理了广义周期时变系统在输出反馈控制作用下的二次稳定性问题·这对于进一步解决广义周期时变系统的H∞控制问题打下了基础·

[1]Lewis F L.A survey of linear singular systems[J].Circuits, Systems and Singular Processing,1986,5(1):30-36.

[2]TakabaK,Morihira N,KatayamaY T.A generalized Lyapunov theorem for descriptor systems[J].Systems and Control Letters,1995,24(1):49-51.

[3]Bolzern P,Colaneri P.The periodic Lyapunov equation[J]. SIAM Journal on Matrix Analysis and Application,1998(4): 499-512.

[4]Bittanti S.30 years of periodic control-form analysis to design [M]∥Proceedings of the Third Asian Control Conference. Shanghai,2000:1253-1258.

[5]苏晓明.广义周期Lyapunov理论及稳定性分析[J].东北大学学报:自然科学版,2003,38(2):141-146.

Quadratic Stabilization forPeriodicallyTime-Varying Descriptor Systems

LÜMingzhu1,L IU Shixun2
(1.Department of Automatic Control,Liaoning TV&Radio University,Shenyang 110034,China;2.CQC North Laboratory(Shenyang)Co.,Ltd.,Shenyang 110141,China)

The problem of quadratic stabilization for periodically time-varying descriptor systems is discussed.By establishing a new Riccati equation,a sufficient and necessary condition is derived for systems to be quadratic stabilization under output feedback control.

periodically time-varying descriptor systems;quadratic stabilization;Riccati equation

TP 13

A

1008-9225(2010)06-0010-03

2010-09-06

辽宁省博士启动基金资助项目(20041024);辽宁省教育厅基金资助项目(202062042)·

吕明珠(1980-),女,辽宁沈阳人,辽宁广播电视大学讲师,硕士·

【责任编辑 刘乃义】