公共资源自主治理二元性的博弈分析——对奥斯特罗姆原则的再认识
汪崇金
(1.山东财政学院,山东济南 250014;2.上海财经大学,上海 200439)
公共资源自主治理二元性的博弈分析
——对奥斯特罗姆原则的再认识
汪崇金1,2
(1.山东财政学院,山东济南 250014;2.上海财经大学,上海 200439)
文章构建了基于公平的囚徒困境博弈模型,从“对未来的重视”和“对公平的关注”两个视角考察了公共资源的自主治理问题。2009年诺贝尔经济学奖得主之一诶莉诺·奥斯特罗姆从长期存续的公共池塘资源的使用制度中所概括出的八个设计原则,正是这两个视角的反映。文章通过对奥斯特罗姆原则的再认识,提出两点启示,即,成功的公共池塘资源使用制度既要明确公共部门与私人部门之间的边界,还要处理好集体选择的二元性,即在集体选择中兼顾公平与效率。
自主治理;集体利益;资源配置;利益分配
一、问题的提出及文献综述
早在古希腊时代,亚里士多德就注意到公地的使用效率问题。加勒特·哈丁 (G.Hardin)在 1968年正式提出了“公地悲剧”的概念,它描述了这样一种情形:因为排他技术或成本的原因,草地往往是开放的,任何人都可以在其上放羊。就某一片草地而言,在某一再生周期,草地上作为饲料的绿草是既定的,一旦羊的规模达到一定规模(即拥挤点),再增加羊的数量就会导致草地的过度使用,在这片草地上放牧的牧民都会因此而受损。从追求个人利益最大化的单个牧民来看,即使草地上羊的数量已经过多(即超过拥挤点),他依然想不断增加放羊的规模,因为草场退化的代价由大家负担。每一位牧民都如此思考时,“公地悲剧”就会不可避免。若真如此,那么就会引发出这样一个悖论,即个人理性的策略会导致集体非理性的结局,也就是说,在公地有效使用的问题上,理性的生灵之间的合作是不可能的,这毫无疑问地抛弃了我们对理性的解释。[1]
与哈丁不同的是,群体理论者相当乐观,并相信,具有共同利益的个人会自愿地为促进他们的共同利益而行动。[2,3]不过,认为从理性的和寻求自我利益的行为这一前提可以逻辑地推出集体会从自身利益出发而采取行动,这种观念事实上是不正确的。[4]除非一个群体中人数相当少,或者除非存在着强制或其他某种特别手段,促使个人为他们的共同利益行动,否则,理性的、寻求自身利益的个人将不会为实现他们共同的或群体的利益而采取行动[4]。也就是说,在有些情况下,牧民会就草地的使用问题而付出行动的。当然,付出行动只是一个前提,而能否实现公共草地的有效使用还涉及到两个层面的问题:即,“制度怎么会得到供给”和“供给什么样的制度”。
第一个层面的问题是制度变迁理论试图要回答的,而这里只考虑第二个问题。传统的作法是:要么将草地私有化、要么对其实施政府管制。人们不禁要问,除此之外是否还别有选择呢?作为公共选择学派创始人物之一埃莉诺 ·奥斯特罗姆 (E. Ostrom),提出了在政府与市场之外的另一个方案。她认为:没有彻底的私有化,没有完全的政府权力的控制,使用者会自主治理公共池塘资源。而且,奥斯特罗姆还基于大量的案例分析,总结了长期存续的公共池塘资源的使用制度所包含的设计原则 (简称为“奥斯特罗姆原则”)。但是,奥斯特勒姆概括出八大设计原则后,并没有深究这些原则所蕴含的逻辑?本文认为,有些公共池塘资源之所以能够长期存续,主要是因为使用制度实现了配置效率与分配公平两大经济目标,即正确处理了集体选择的二元性。奥斯特罗姆虽然在实证分析之前构建了“自筹资金的合约实施博弈”模型,但这一理论模型并未涉及利益分配问题。因此,构建一个与设计原则一致的理论模型就成为本文的目标。
从博弈论的视角分析公共池塘资源的努力早已有之,公地悲剧早已被形式化为一个囚徒困境博弈,[5]但在囚徒困境无限次重复博弈中,公地悲剧是可以避免的。具体而言,如果每个牧民都认识到在以后的再生周期里,他们还会在这片草地上放羊,而且每个牧民都有足够的耐心,那么,任何短期的机会主义行为的所得都是微不足道的,每个牧民就会有积极性为自己建立一个乐于合作的声誉,同时也有积极性惩罚对方的机会主义。可惜的是,与奥斯特勒姆的理论模型一样,无限次重复的囚徒困境博弈并未纳入公平因素。本文参照诺齐克有关平均主义社会福利函数的设定,[6]构造一个包含公平的效用函数,并应用到无限次重复的囚徒困境博弈中,为奥斯特勒姆原则提供一个理论分析框架,试图藉此框架而对奥斯特罗姆所概括的八个原则给与重新认识,并从中获得一些启示。
二、模型
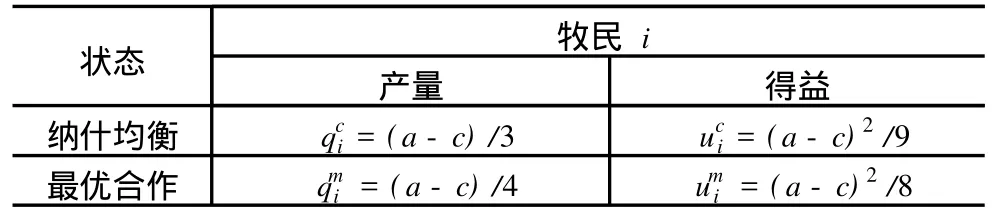
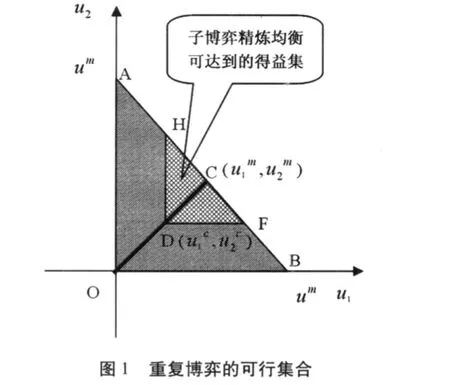
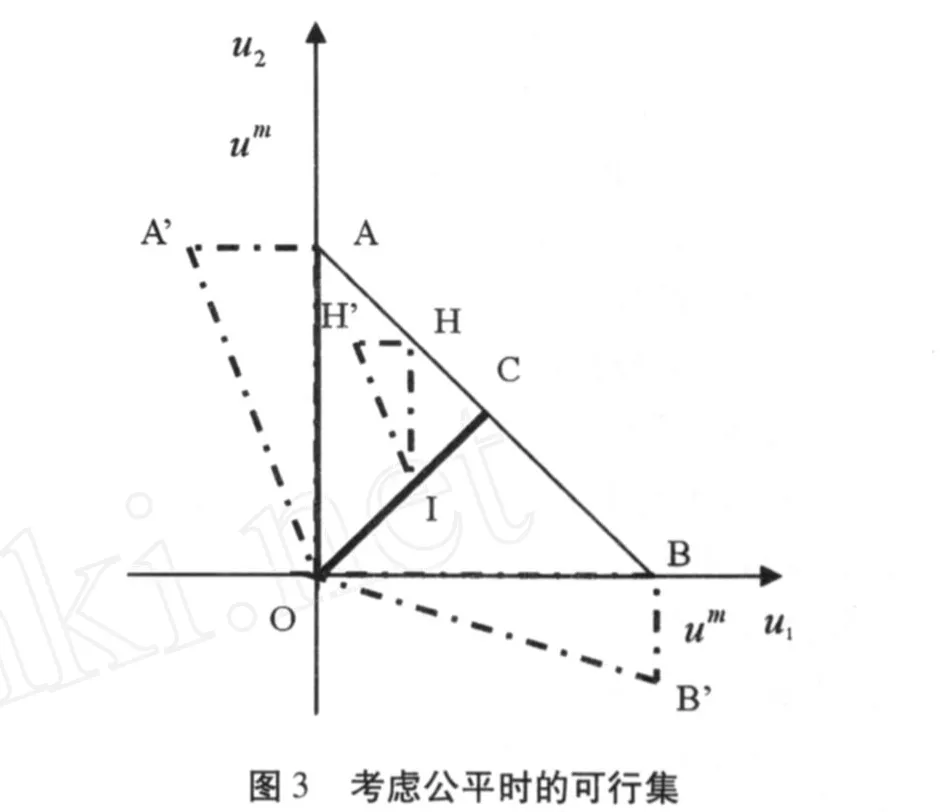
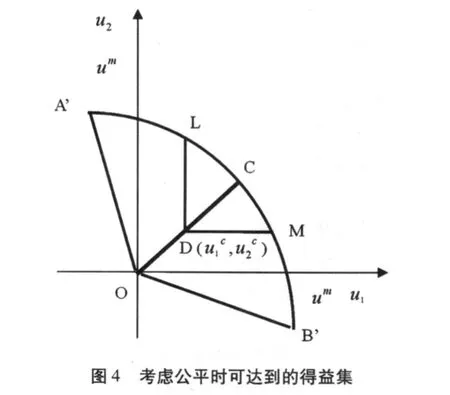
假设有两个牧民共同拥有一片草地,每年春天,牧民要决定自己的养羊规模,用 gi∈[0,∞)表示,其中,i=1,1;而 G=g1+g2,代表该草地上放养羊的总量;v代表每只羊的平均价值,v是 G的一个函数,具体为 v=v(G)=a-G,其中,a代表该草地上能够承受的最大放养量;并且假设 c为养羊的平均成本,且c< 其中,βi≥0表示牧民 i对不利于自己的不公平的关注程度,这里称之为对不公平的厌恶系数。下面就βi=0和βi>0两种情况分别给与讨论。 1.βi=0的情况 βi=0,亦即不考虑公平的情况。我们通过简单的计算容易获得每个牧民在各自为政(即纳什均衡)状态下的产量和得益、以及两人在实现最优合作状态下的产量和得益。详见表 1。 表1 纳什均衡与最大合作状态 从上表可以看出,从最优合作状态到纳什均衡状态,草地上的羊群总规模变大,但得益却减少,也就是说,草地的使用效率下降了;而且,随着羊的平均价值的提高(如市场需求随人口的增长而增加)和平均成本的下降(如成活率随科技的进步而提高),草地的使用效率下降的程度会更明显。显然,通过减产回到最优合作状态对双方都有利,但任何纳什均衡状态下的牧民都不会单方面减产,这就是一次性博弈中的“囚徒困境”。 不过,“囚徒困境”的难题可以在无限次重复博弈中解开。考虑两个牧民都采用下列“冷酷战略”:开始选择合作,即选择最优合作状态下的产量,直到对方选择了不合作,则选择纳什均衡状态下的产量,然后永远选择不合作。 在讨论重复博弈时,必须引入贴现因子δ,即考虑得益的时间价值。经过简单计算可得,当δ≥δ*= 9/17时,任何一位牧民都不会为谋求某一期多一点的收益而愿意承担以后各期的惩罚。也就是说,通过采用上述“冷酷战略”,两牧民能够达成一致的默契,以实现最优的合作。 上述结论只是“无名氏定理”的特例。推而广之,“无名氏定理”告诉我们,在无限次重复博弈中,如果参与人有足够的耐心,即贴现因子足够大,那么任何可行的个人理性得益都可以通过一个特定的子博弈精炼均衡得到。[7]其中,个人理性即为参与人的保留得益或最小最大得益,由下式定义: 参与人 i的最小最大得益是他的对手选择任何q-i时,只要参与人 i正确预见到 q-i并对它做出最佳反应就能得到的收益下限。在本博弈中,无论对手选择多大的放养规模 q-i,牧民的最小最大得益为=(a-c)2/9。图 1中,ΔAOB为可行集,而ΔDFH为可行的个人理性得益集合,按照“无名氏定理”,只要δ≥δ*=9/17时,在无限次重复博弈中,处于ΔDFH区域的得益都可以通过一个特定的子博弈精炼均衡得到。其中对角线与AB线的交点 C刻画的正是上文所述的最大合作状态。 现在考虑贴现因子δ<δ*时,判断图 1中子博弈精炼均衡可达到的得益集如何变化。注意,图 1中每个点都映射了一个行动组合和一个最小的贴现因子,而且,在无限重复博弈中要实现 FH线上不同的最大合作状态,对应的最小贴现因子也是不同的。 在对称状态下,按照上述δ*的计算过程,可以发现,当δ<δ*时,两牧民也可以通过采用类似的“冷酷战略”实现低水平的合作。这意味着当δ<δ*时,C点的某一邻域与可达到的得益集的交集将不再能够通过子博弈精炼均衡得到,图 2近似描述了这种情况。而且,随着δ不断变小,该交集的范围越来越大。 2.βi>0的情况 假设在不考虑公平时某一个子博弈精炼均衡达到的得益组合为图 3中的 H点,现在,我们来考察在效用函数中纳入公平后,该得益组合将如何变化。由于 H点描述的状态是对牧民 1不公平的,按照公式 1,牧民 2的得益不会改变,而牧民 1的得益变化额为不公平程度与厌恶系数的乘积。在图 3中,H I为不公平程度,∠H I H’的斜率为厌恶系数,而 HH’即为考虑公平后牧民 1得益的变化量。同理,A’和B’点所描述的状态分别对应于 A和 B点,其中,∠AOA’和∠BOB’斜率分别为的β1,β2。推而广之,考虑公平时,可行集将不再是图 1中的AOB,而变成图4中OA’、OB’和曲线A’CB’围成的区域,该区域随着βi值的变化而变化。值得注意的是,在对称状态下,即使纳入公平的概念,前后没有变化。 下面我们来分析考虑公平的牧民的最小最大得益。在上述“冷酷战略”下,牧民 i至少可以选择与牧民 j相同行动,同βi=0时的情况一样,牧民 i的最小最大得益仍然是=(a-c)2/9。因此,在无限次重复博弈中,子博弈精炼均衡可达到的得益集如图 4中LDMC围成的区域,其中,D和 C点是固定不动的,而L点和M点的位置分别由β1和β2决定。具体而言,给定贴现因子δ的值,随着βi的增大,可达到的得益集的边界CL、CM将绕C点向左下方收缩。 综合上述就βi=0和βi>0两种情况的讨论,我们发现:在参与方采用“冷酷策略”的无限次重复博弈中,子博弈精炼均衡可达到得益集受两个因素的影响,这两个因素分别为表示对未来重视程度的δ和体现对公平重视程度的β。应用到本文中,也就是说,如果牧民对未来收益评价的下降或对不利自己公平的更加地关注,通过“冷酷策略”实现自主治理的可能性都将变小。 结合上文分析,可以发现,奥斯特罗姆从长期存续的公共池塘资源的使用制度中概括出来的八个原则,要么增强参与各方对未来收益的重视程度,要么会促成参与各方达成相对公平的操作规则,还有可能有利于两者的实现。下面,我们利用奥斯特罗姆提及的成功或不成功的案例对这一发现给予佐证。 “囚徒困境”式难题之所以能在无限次重复博弈中得以解开,关键是引入贴现因子的概念,贴现因子度量了参与方对未来收益的评价,而贴现因子的大小受多种因素的影响。在公共池塘资源使用问题上,其边界是否清晰界定 (原则 1)是决定贴现因子大小的一个关键。如奥斯特罗姆所言,“不界定公共池塘资源的边界,不能限制‘外来者’的进入,当地占有者就面临着他们经过努力创造的成果被未作任何贡献的其他人所获取的风险。……那些投资于公共池塘资源中的人将得不到预期的回报”;“如果无论当地占用者采取什么行动,公共池塘资源都会被其他人的行动所毁坏,那么即使那些多年来一直对自己获取公共池塘资源的量加以限制的人,也会开始给予未来收益很高的贴现率”。[8]在瑞士的托拜尔,早在 1224年,社群拥有的财产的边界就以法律的形式给与确定。[8]其他成功的案例也都无一例外地满足这一原则。 在公共池塘资源的边界得以明确后,有理由相信人们能够接受一个使自己受益的规则,但是,“事先同意遵守规则是一个易于作出的承诺,事后能实际地遵守规则,尤其是在机会主义诱惑很强的情况下也能如此,才是有意义的成就”,[8]所以,切实可行的监督和制裁成为必须。原则 4要求监督者或是占用者本人、或是对占用者负有责任的人。原则 5要求进行分级制裁,即违规者可能受到其他占用者、有关官员或他们两者的分级制裁。对公共池塘资源的占用者一般来自相对稳定的社群,如果有人违规,应该按违规的严重程度决定制裁的大小,有时可能只是一个口头的警告,有时可能是被要求给监督者缴纳少量罚金,除非遇上重大违规行为才被诉诸整个社群。显然,这样的分级制裁形式一方面不会激化社群内部的矛盾,另一方面使得处罚的威胁更具可信性。当然,分级制裁需要赋予监督者一定的裁量权,而且在大多情况下还允许监督者从罚没品中分得一部分,因为这样会给监督者一定的激励,但是,如果监督者不受占用者有效监督,监督者对违规行为的无视或寻租将不可避免。 机会主义行为尤其是搭便车是集体行动的主要挑战,上面所讨论的三个原则都从资源配置的视角展开的,这些原则有利于增强占用者对未来收益确定性的信念,从而避免机会主义行为的发生,提高实现私人合作和自主组织的可能性。不过,即使合作会产生净收益,如果利益分配不尽人意,合作也可能难以维系。奥斯特勒姆原则的另一个视角正是利益的分配。 首先,使占用和供应规则与当地条件保持一致(原则 2)是实现公平的需要。例如,在托拜尔和瑞士一些拥有社群土地的村庄,对砍伐树木程序做出如下的规定:第一步由村庄里的管林人对准备砍伐的树木打上标记;第二步是有资格获取原木的家庭组成砍伐队,并平等地分摊砍树、拖运原木和把这些原木堆成大体相等的木垛等工作;然后采用抽签的方法把这些木垛分配给有资格的家庭。[8]在日本,村庄对每个家庭在为维护公地而分摊的、参加集体劳动的义务有明文规定。……每一户所作的贡献都记录在案,以确保每个家庭都不逃脱它应尽的责任。只有生病、遭遇不幸和没有身强力壮的成年人的家庭,才有理由免于参加集体劳动。[8]显然,这些作法都是会实现利益的公平分配而设计的。 随着知识的积累、环境的变迁或其他因素的影响,有人可能会发现事先同意遵守的规则并未实现其预计的收益,如果规则不予修正,其遵守规则的自觉性必然下降,甚至会主动破坏既定的规则。按照原则 3,他有权提议修改对其不利的操作规则。只要他的提议被广泛的、公正的讨论,无论提议是否被采纳,他一般都会尊重经公平协商的结果。由此可见,原则 3能够确保占有各方对公共事物的关注并对自己行为负责。 无论是规则的制定或修改,还是制裁程度的确定,都涉及到许多价值观念不同、彼此利益冲突的个人,要他们在某一问题上达成完全一致的认识是困难的,分歧更是在所难免,因而以较低成本解决分歧的机制也就成为必须,这正是原则 6的内容。 图 5 奥斯特罗姆原则的重新归类 若要把奥斯特勒姆归纳的八个原则在私人部门和公共部门之间划分,则可用图 5来表示。前五个原则在私人部门内自成系统,朝着“增强参与各方对未来收益的重视程度”和“促进参与各方达成相对公平的操作选择”两个目标逐层推进,而原则 6进一步保证两个目标实现。 原则 7是指向公共部门的,由于政府很难收集到关于资源分布、个体行为等在特定时间和特定地点的局部知识,特别是在复杂的公共资源使用制度设计中,这些知识又是重要的,与此相反的是,占用者具有更多的信息优势,他们设计的制度往往更具操作性,因此,占用者设计自己制度的权利不受外部政府权威的挑战。马维尔渔场的使用制度为我们提供了一个反面的例子,在位于斯里兰卡南端的马维尔渔场的渔民曾设计出相当漂亮的规则,以对进入海滩和使用海滩围网进行了有效的管制。遗憾的是,原则 7没有得到有效地执行,当地官员掌握着审批新网的权力,随着当地人口的增长以及鲜鱼市场价格的大幅上涨,官员们屈从于在选举中投赞成票的许诺,对围网控制的多次尝试都没有成功。 面临更复杂的公共池塘资源使用制度设计时,需要在一个多层次的分权制企业中,对占用、供应、监督、强制执行、冲突解决和治理活动加以组织,从而进一步确保了规则体系的稳定性,而这些工作不仅涉及公共部门还涉及私人部门,所以把原则 8放在代表公共部门和私人部门的两个椭圆交集区域。 本文将公平概念纳入无限次重复的囚徒困境博弈模型中,利用无名氏定理,分析了在无限次重复博弈中“冷酷策略”实现子博弈精炼均衡的两个影响因素,即表示对未来重视程度的δ和体现对公平重视程度的β。文章还沿着上述两个视角将奥斯特罗姆所归纳的八个原则重新归类。基于上文的模型分析和对奥斯特勒姆原则的再认识,本文得到如下两点启示。 第一,在公共池塘资源使用的成功案例中,公共部门和私人部门既分工又合作 (如图 5所示),而不是按照传统的、非此即彼的划分公、私部门的界线,这正是奥斯特勒姆所提出的第三条路的特征所在。具体而言,在简单的案例中,由于占用者具有制定规则、监督惩罚等方面的信息优势,政府不应干预占用者设计自己的制度。例如,设计近海渔场的捕捞次序时,只有当地渔民才知道渔场资源的分布特征,而政府官员一般是没有这方面的信息积累的,因此在组织工作方面也就没有优势可言,即使由他们设计的规则在实践中也难以得到有效地实施,从这个意义上看,政府官员在工作中应理所当然地多听取民众的意见。当然,讲到自主治理,并不是说政府无所作为。比如在占用者自发行动时,政府应在响应民意的基础上提供诸如信息搜集、技术论证等具有公共产品性质的服务;在较为复杂的案例中,政府还有必要与私人部门合作,形成多层次的分权制企业,共同作为,进一步稳固合作基础。 第二,公共池塘资源的合理利用是一种集体利益的实现,无论集体选择的内容与形式如何,任何一种类型的集体选择客体都包含两方面的属性:反应集体整体与自然之间相互关系的资源配置以及集体内部人与人之间相互关系的利益分配,而本文的两个视角正是集体选择二元性的充分体现。[9]长期存续的公共池塘资源使用制度一方面降低了交易费用,实现了资源的有效配置,另一方面从规则层面上维护着集体内部的公平分配,两者相辅相成,前者的实现使参与各方认识到集体利益的存在,而后者有利于自主组织的稳定存续。 [1]Campbell,R..Background for the Uninitiated. In Paradoxes of Rationality and Cooperation,eds.R.Campbell and L.Sowden,Vancouver:University of British Columbia Press. 1985:pp.3-41. [2]Bentley,A..The Process of Government.Evanston, I11.:Principia Press,1949. [3]Truman,D.B..The Governmental Process.New York:Knopf,1958. [4]曼瑟尔·奥尔森.集体行动的逻辑[M].上海:格致出版社,上海人民出版社,1995. [5]Dawes,R.M..The Commons Dilemma Game:An NPerson Mixed-Motive Game with a Dominating Strategy for Defection.OR IResearch Bulletin 13.1973:1-12. [6]毛程连.中高级公共经济学[M].上海:复旦大学出版社,2006. [7]朱·弗登博格,让·提诺尔.博弈论[M].北京:中国人民大学出版社,2002. [8]诶莉诺·奥斯特罗姆.公共事物的治理之道:集体行动制度的演进[M].上海:上海三联书店,2000. [9]曾军平.自由意志下的集团选择——集体利益及其实现的经济理论[M].上海:格致出版社,上海人民出版社,2009. F062.6 A 1008-2670(2010)05-0013-06 2010-09-10 山东省社科规划项目《基本公共服务均等化问题研究》(09CJGZ37)。 汪崇金,男,安徽桐城人,山东财政学院财税与公共管理学院讲师,上海财经大学博士研究生,研究方向:公共经济学。 (责任编辑:赵 利)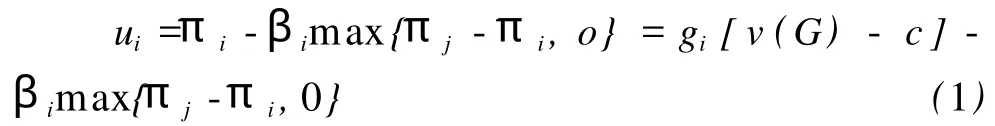
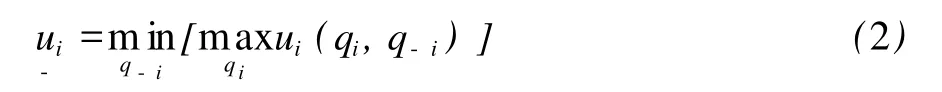

三、对奥斯特罗姆原则的再认识

四、结论与启示

