基于浆体的泥石流容重计算

陈宁生 杨成林,3 李 欢

(1.中国科学院山地灾害与地表过程重点实验室,成都610041;2.中国科学院水利部成都山地灾害与环境研究所,成都610041;3.中国科学院研究生院,北京 100049;4.四川大学,成都 610065)

泥石流是山区介于挟沙水流和滑坡之间的土(泛指固体松散物质)、水、气混合流体,其固体颗粒粒径分布广,不均匀系数(控制粒径d60和有效粒径d10的比值)多在100以上,黏性泥石流甚至达到1 000以上[1]。泥石流组成的复杂性导致了对其研究的困难。为了简化泥石流体的结构模式,通常将泥石流分为两部分:即浆体(液相)和较粗的砂石固体颗粒(固相),分别研究各部分对泥石流体运动的影响就相对容易些。只要确定出浆体的最大颗粒直径,即上限粒径d0,泥石流的液相和固相组成就可容易得到;只要确定出浆体的容重和泥石流的颗粒组成,泥石流的容重也容易得到。因此,上限粒径和容重是泥石流浆体的两个主要特征参数。

现有的泥石流容重计算方法有数十种之多,概括起来为理论推导法和特征参数法两类(表1)。理论推导法主要用于理论分析和室内泥石流试验,也运用于可以观测的泥石流;但自然界中可以直接观测取样的泥石流沟极少,因此实际中依然采用野外调查和访问目击者的方法,所得容重受人为因素影响大,精度不确定。对于无法通过目击者得到可靠特征的泥石流,许多学者通过统计分析一定阵次的泥石流,得出了容重与泥石流沟相关特征参数的关系,提出了关于角砾含量[2]、颗粒平均粒径[3]、黏粒含量[4]、中值粒径[5]、算术平均粒径[5]和主沟坡降[6]等单因素经验公式,也提出了关于松散物质储备量、补给区和流通区比降、流域面积、固体物质岩性和补给方式的多因素经验公式[6]。这些经验公式或缺乏理论依据,或有一定的区域性,单因素经验公式还存在单一性。在实际工作中,人们希望找到既有理论依据,又实用的方法来计算泥石流容重。

本文首先推导出泥石流浆体容重和细颗粒含量与泥石流容重的理论关系,接着分析出浆体容重和细颗粒含量的确定取决于泥石流浆体上限粒径的选择。通过分析发现泥石流暴发时在沟道、岩壁留下的固体黏结物与泥石流浆体部分组成一致,提出一种确定泥石流浆体上限粒径和容重的

方法,最终得到一种实用的基于泥石流浆体的容重计算方法。

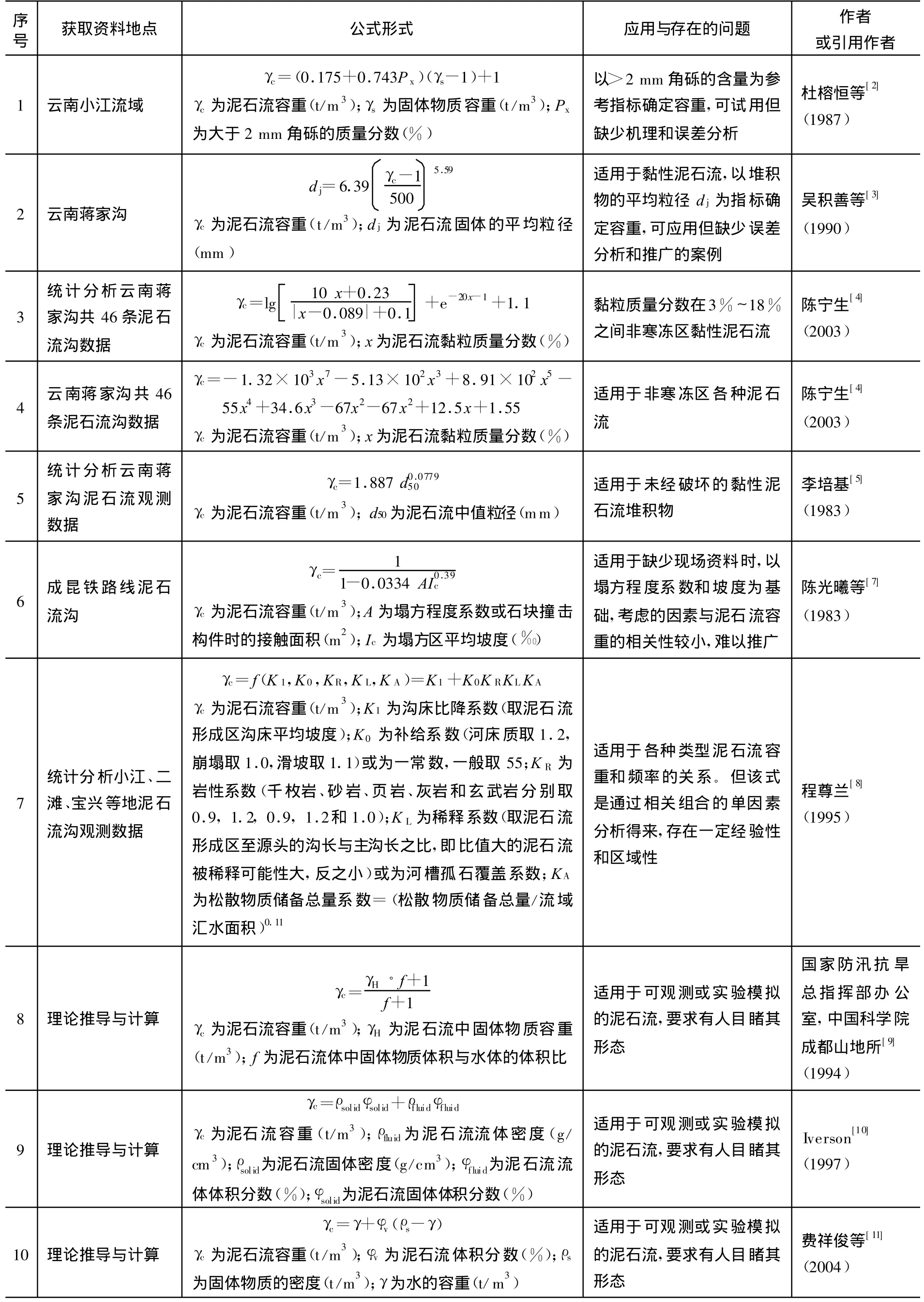
表1 常用的泥石流容重计算公式Table1 General formula for bulk density of debris flow

1 模型建立

泥石流浆体是由于水的强烈紊动或者由于细微颗粒巨大的亲水表面上结合水膜分子力的作用,使相当一部分较细颗粒同水混合或结合成一个似均质的流体,它们在运动中不相分离,甚至在静止后也分离较慢。泥石流浆体通过细颗粒部分影响泥石流颗粒组成,进而影响泥石流容重,故而通过浆体的容重推求泥石流容重是可行的。

1.1 建立模型

同浑水(含泥沙的水)相似,在泥石流中固体颗粒和水与容重满足[12]

其中 :γc分别为泥石流体的容重(t/m3);ρw 和 ρs分别为水和固体物质的密度(t/m3);C vt为泥石流中固体的体积分数。

类比公式(1),得到泥石流容重 γc与泥石流体固相和液相的关系

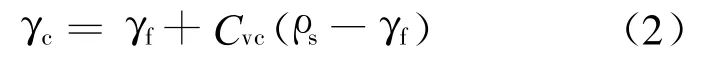
泥石流浆体容重γf与浆体中固体和水的关系

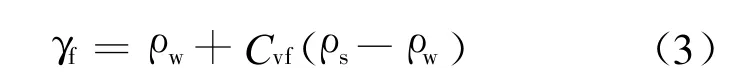
其中:C vc,C vf分别为固相体积分数和液相体积分数;γf为泥石流浆体的容重(t/m3)。

在泥石流浆体容重γf相同时,粗颗粒含量对泥石流容重 γc起主要作用。令粗颗粒在全部固体中的质量分数为w,则满足

通过式(1)～(4),得[11]

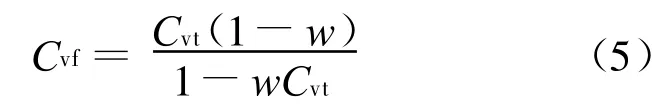
在实际调查中,细颗粒的质量分数w′=1-w更易获得。以细颗粒的质量分数w′代入式(5),以 γw=1.0 t/m3代入式(1),由式(1)、(3)、(5)得泥石流浆体容重γf与泥石流容重γc的计算公式

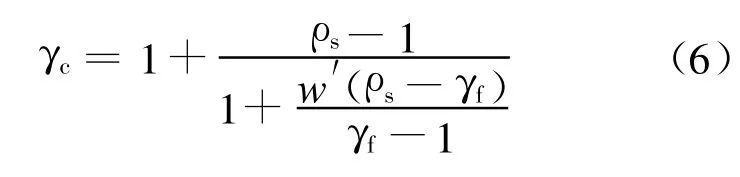
1.2 参数确定

由式(6)可知,当固体颗粒物质密度ρs为一定值时,泥石流体容重γc仅是细颗粒的质量分数w＇和浆体容重γf的函数。如图1(其中粗线依次取w′=0.1,0.3,0.5,0.7,0.9;细线依次取w′=0.2,0.4,0.6,0.8),取 ρs=2.65 t/m3,有以下结论:

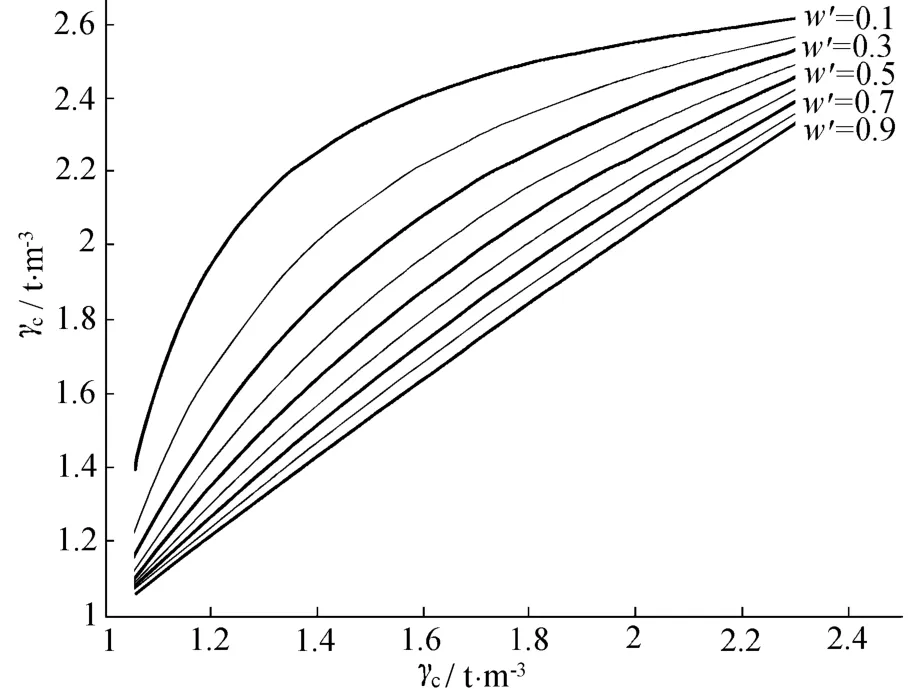
图1 泥石流容重随浆体容重、细颗粒质量分数变化图Relationship among fine particle content,bulk densities of debris flow and slurry

a.泥石流浆体容重一定时,泥石流中粗颗粒的质量分数(1-w′)对泥石流容重起决定作用,且粗颗粒的质量分数(1-w′)越高,泥石流容重增幅越大。

b.泥石流中粗、细颗粒的质量分数不变时,泥石流体容重随浆体的容重(主要受含水量的影响)的增加而增加,但增幅变小。

c.泥石流浆体容重随细颗粒的质量分数的增大而增大,细颗粒的质量分数越高,容重增幅越小。

由以上分析可知,若确定出细颗粒的质量分数w′和浆体容重γf,则泥石流体容重很易求得。在实际工作中,如果已知泥石流浆体上限粒径d0,由泥石流固体中粒径≤d0的颗粒质量与泥石流固体颗粒总质量之比即为细颗粒的质量分数w′,故细颗粒的质量分数w′转换为泥石流浆体上限粒径d0的确定;上限粒径d0的选取决定了泥石流浆体的物质组成,浆体物质组成决定浆体容重γf,故上限粒径d0对泥石流浆体容重γf也有重要影响。因此,上限粒径d0成为确定泥石流容重的关键。

1.2.1 上限粒径的确定

上限粒径d0是个变量,对于不同的泥石流沟,泥石流浆体上限粒径值是不同的;即使是同一条沟,不同的发展阶段、阵次也会有所差异。随着上限粒径d0的增加,泥石流容重γc也会提高。费祥俊等利用蒋家沟的泥石流观测资料[13],提出分别以d0=0.05mm和2.0mm作为泥石流上限粒径;沈寿长等提出力学平衡计算模型[14],计算某一黏性泥石流的上限粒径为0.3 m。

在泥石流运动过程中,固体颗粒由于粒径的不同呈现出悬浮、跃移和推移等不同的运动方式。泥石流浆体中的固体颗粒绝大部分呈悬移状态,并且浆体会在沟道、岩壁上黏附,这种固体黏结物与泥石流浆体颗粒组成十分接近。

从力学性质分析,泥石流浆体容重大于水的容重,可以极大地降低颗粒的有效重力。泥石流浆体通常看作宾汉体,它具有一定的屈服应力。泥石流浆体由细颗粒(d≤0.05 mm)浆体和较粗沙粒组成,因此屈服应力主要由细颗粒的黏结力和较粗颗粒间的黏性摩擦力组成,王裕宜等研究表明[15],影响屈服应力的主要因素是颗粒的组成和含量,它随着较粗颗粒含量的增大而增大,同时随着细颗粒比例的减小而减小。屈服应力的存在使浆体有一定的挟沙能力。由颗粒表面所受浆体的屈服应力的合力与颗粒的有效重力平衡,可以得出浆体所能挟持的固体颗粒最大粒径值dM。当泥石流泥位下降时,沟壁浆体的表面颗粒所受屈服应力降低,固体黏结物中的最大粒径 d m＜dM,且泥石流中d≤dm的颗粒都在固体黏结物中,若以d≤d m的颗粒作为浆体的组成部分,则泥石流浆体更为均质。因此,本文提出以固体黏结物中的最大颗粒d m作为泥石流浆体的上限粒径d0,即 d0=d m 。

1.2.2 浆体容重和细颗粒含量的确定

当泥石流浆体的上限粒径d0确定以后,浆体的容重γf和泥石流细颗粒的质量分数w′是容易确定的。

首先是浆体容重γf的确定。当泥石流固体黏结物中的最大粒径d m确定后,上限粒径和浆体的固体颗粒组成已知,即可在现场利用简单工具配制泥石流浆体。最终确定的泥石流浆体必须满足颜色、屈服应力一致的原则。屈服应力一致指在同一倾角和性质的岩壁(或沟道)上,配制的泥石流浆体黏附在岩壁上的形状、厚度与现场一致。此时的容重即为该次泥石流浆体的容重(γf)i。一般取多次(≥3)以上容重值的平均值为确定的浆体容重γf。

此时,泥石流细颗粒的质量分数w′的确定只需较为完整的泥石流固体堆积物即可,一般采用坑探的方式取得。大量研究发现,同一泥石流沟中,不同场次和不同地点泥石流的细颗粒含沙量并无显著差异,因此,泥石流浆体的上限粒径d0即可作为下游泥石流堆积物中粗细颗粒的分界点。粗细颗粒分界点确定后,就可确定细颗粒的质量分数w′,最后根据理论公式(6)就可得出泥石流体的容重 γc。

1.3 适用范围和优点

理论公式(6)适用于任何性质的泥石流容重计算。就实际应用中,将泥石流沟边壁、岩壁的固体黏结物的最大粒径作为上限粒径对黏性泥石流有一定的现实性;在稀性泥石流中,取得的泥石流浆体容重误差较大,影响泥石流容重的精度。

同已有的泥石流容重计算方法相比,基于泥石流浆体的容重计算方法有明显的优点:

a.本方法以式(6)为理论基础,配合现场调查所得的特征参数,计算出的容重较之单纯的特征参数法准确性要高。

b.单纯的理论公式多用在理论分析和室内的泥石流试验,特征参数法的原始样本资料来自有限的区域,方法的使用有一定的区域限制;而基于泥石流浆体的容重计算方法有更广泛的通用性。

2 计算实例

2.1 基于浆体的泥石流容重计算

本文通过四川省木里县麦地龙乡杨房沟的泥石流容重计算作为应用实例。杨房沟为雅砻江的一级支流,位于麦地龙乡上游约6 km的雅砻江左岸,本文计算的是其1993年发生的特大泥石流的容重。由现场考察得到该次泥石流坑探堆积物和岩壁黏结物的颗粒分析见表2。

其中,岩壁黏结物的最大粒径d m为3.0 cm,即上限粒径d0=3.0 cm;配制浆体使满足颜色和黏结力一致性原则,获得的浆体容重1.80 t/m3;坑探堆积物中细颗粒含量w′=0.6556,ρs=2.65 t/m3,计算得

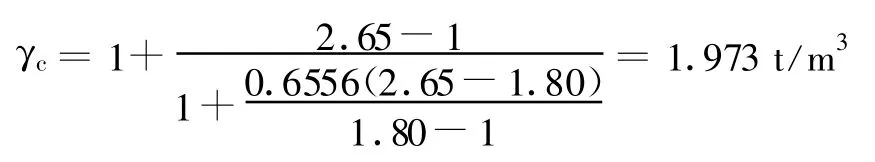
表2 杨房沟泥石流颗粒组成分析结果(w/%)Table2 Grain-size distribution of debris flow in Yang fang Gully of Yalong River

2.2 现场配制容重

现场目击者确定泥石流浆体浓度,用现场泥石流堆积物配制原状泥石流样,直到目击者认可为准。采用直径为30.0 cm、高度为30.1 cm的圆柱形铁桶。并现场称取配制浆体的质量,测量体积,获得泥石流容重。先后进行2次试配:

a.配置泥石流体的体积为10 667.0 cm3,相应的浆体质量为21.6 kg,计算容重γc=2.025 t/m3。

b.配制的泥石流的体积为10 800.0 cm3,相应称得浆体质量为20.7 kg,计算容重γc=1.917 t/m3。

2.3 特征参数法

选取具有代表性、对于杨房沟特征参数容易求得的方法列于表3。可以看出基于浆体的泥石流容重计算法与公认的较为准确且运用最多的现场配制法计算值相当接近,在运用中具有明显的优势。同时,采用蒋家沟观测资料对基于浆体的泥石流容重计算法进行验证,计算结果也与实测值相近。

表3 特征参数法与基于浆体法得到的容重值比较Table3 Comparison of bulk densities for debris flow based on characteristic parameter and slurry method

3 结论

a.基于浆体容重的泥石流容重计算公式,是一种理论性和经验性相结合的新方法,体现了泥石流浆体浓度和固体颗粒的组成决定泥石流容重的变化。粗颗粒含量愈高,泥石流容重提高幅度愈大;随着浆体容重的提高,泥石流容重增幅减小;随着细颗粒含量的增加,泥石流浆体容重的增幅也减小。

b.由于泥石流暴发在时间和空间上的差异,泥石流浆体的上限粒径是个变值。本文提出以固体黏结物中的最大颗粒作为泥石流浆体的上限粒径。

c.通过实例的计算对比,说明本文提出的基于浆体容重的泥石流容重计算方法,适用范围广,准确度高。

d.泥石流浆体的上限粒径决定浆体的性质,如何得到其准确值,其影响因素有哪些,这些因素是如何影响上限粒径值的,这些问题都有待进一步研究。

[1]韩慕吾.泥石流容重的确定[J].水土保持通报,1985,2(1):48-50.

[2]杜榕恒,康志成,陈循谦,等.云南小江泥石流综合考察与防治规划研究[M].重庆:科学技术文献出版社重庆分社,1987:99-100.

[3]吴积善,康志成,田连权,等.云南蒋家沟泥石流观测研究[M].北京:科学出版社,1990:131-132,60-61.

[4]陈宁生,崔鹏,刘中港,等.基于黏土颗粒含量的泥石流容重计算[J].中国科学:E辑,2003,33(增刊):164-174.

[5]李培基,梁大兰.泥石流容重及其计算[J].泥沙研究,1982,9(3):75-83.

[6]唐邦兴.中国泥石流[M].北京:商务印书馆,2000:38-39.

[7]陈光曦,王继康,王林海.泥石流防治[M].北京:中国铁道出版社,1983:22-77.

[8]程尊兰.泥石流设计流量中容重的计算方法[C]//泥石流(4).重庆:科学技术文献出版社重庆分社,1995:95-97.

[9]国家防汛抗旱总指挥部办公室,中国科学院水利部成都山地灾害与环境研究所.山洪泥石流滑坡灾害及防治设计[M].北京:科学出版,1994:169-183.

[10]IVERSON RM.The physics of debris flow[J].Review s of Geophysics,1997,35(3):25-296.

[11]费祥俊,舒安平.泥石流运动机理与灾害防治[M].北京:清华大学出版社,2004:39-40,105-125.

[12]钱宁,万兆惠.泥沙运动力学[M].北京:科学出版社,1983:35.

[13]费祥俊,康志成,王裕宜.细颗粒浆体、泥石流浆体对泥石流运动的作用[J].山地学报,1991,9(3):143-152.

[14]沈寿长,谢慎良.泥石流体的结构模式和粗颗粒对泥浆体流变特性的影响[J].泥沙研究,1983,9(3):12-19.

[15]王裕宜,詹钱登,严璧玉,等.泥石流体结构和流变特性[M].长沙:湖南科学技术出版社,2001:216.