颗粒失效对SiC增强铝基复合材料屈服应力的影响模型

宋 旼，谢灿强，贺跃辉

(中南大学 粉末冶金国家重点实验室，长沙 410083)

众所周知，在铝合金中添加SiC颗粒或SiC短纤维将增加材料的屈服应力和弹性模量。早期的研究[1−5]表明：这种强化效应主要取决于两种因素。第一种因素称之为剪切滞后效应，最早由COX[1]提出，随后得到了NARDONE等[2−5]的发展。剪切滞后模型的物理原理基于铝合金基体将外部所施加的应力传递到硬的SiC增强体上，从而导致复合材料屈服应力和弹性模量的提高。第二种因素称之为淬火强化效应，由ARSENAULT等[6−8]提出。淬火强化效应的物理原理基于由于铝合金基体与SiC增强体有不同的热膨胀系数，在热处理过程中将会产生大量的位错增殖，从而导致复合材料屈服应力和弹性模量的提高。

然而，无论是剪切滞后模型还是淬火强化理论都没有考虑到复合材料所具有的两个重要特点，即时效加速现象和颗粒失效对复合材料屈服应力的影响。模拟复合材料的时效加速现象非常困难，主要源于量化析出相非均匀形核与长大这一热力学和动力学过程的困难。最近，本文作者通过考虑位错的管道扩散效应，成功地发展了SiC增强铝基复合材料时效加速现象的多尺度力学模型[9]。模型的计算结果与 SiC增强的Al-Mg-Si合金复合材料的实验结果吻合较好。

到目前为止，国际上还没有一个关于计算SiC颗粒失效对复合材料屈服应力影响的有效的力学模型。实际上SiC颗粒失效(包括SiC颗粒脱粘与颗粒断裂)是SiC增强铝基复合材料在变形过程中存在的普遍现象。忽略颗粒失效对复合材料屈服应力的影响将直接导致计算结果与材料实际强度出现偏差。计算SiC颗粒失效对复合材料屈服应力影响的主要困难在于量化失效颗粒体积分数的困难。早期研究[10−13]表明，颗粒脱粘以及颗粒断裂均可以采用 Weibull统计分布来计算。但是采用 Weibull统计分布计算颗粒失效需要知道SiC颗粒在变形过程中的承载大小。WITHERS等[14]指出，SiC颗粒以及SiC短纤维在变形过程中的承载大小可以采用 Eshelby等效夹杂理论计算。因此，从以上分析可知，通过合适的方法结合 Weibull统计分布和等效夹杂理论为计算颗粒失效对复合材料屈服应力的影响提供了可能。

本文作者基于修正的剪切滞后模型与淬火强化理论，结合Weibull统计分布与Eshelby等效夹杂理论，发展了一个新的SiC增强铝基复合材料屈服应力的综合力学模型，从复合材料的微观组织预测宏观的力学性能。新发展的模型可以预测SiC颗粒体积分数、尺度以及长径比对复合材料屈服应力的影响，为发展具有高屈服应力的SiC增强铝基复合材料提供了理论依据。同时采用一系列相关实验对新发展模型的准确性进行了验证。

1 模型发展

1.1 修正的剪切滞后模型

修正的剪切滞后模型[2−3]指出，复合材料屈服应力的提高源于基体材料将外加载荷传递到硬的增强体。对于SiC增强的铝合金复合材料来说，屈服应力可以表示为[2−3]

式中：A为SiC增强体的长径比；fp为SiC增强体的体积分数；fm为基体铝合金的体积分数；σmy是基体铝合金的屈服应力；Δσor=2Gb/L为位错绕过SiC颗粒所引起的屈服应力的增加(即 Orowan强化机制)，其中L=0.6d(2π/fp)1/2是SiC颗粒的间距；b是位错的泊氏矢量，G是基体铝合金的剪切模量[8]。

基体铝合金的屈服应力(σmy)，可以通过考虑基体铝合金的本征屈服应力(σin)，淬火强化效应(σqs)，晶粒细化强化效应(σgrs)以及几何必须位错强化效应(σgnds)得到。因此，式(1)可表示为

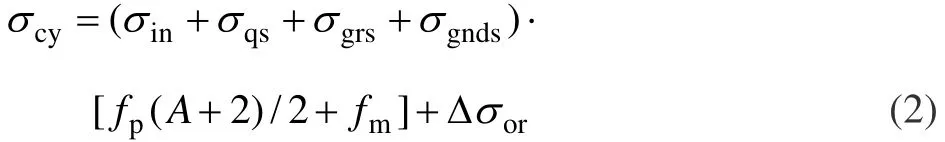
淬火强化效应(σqs)来源于基体与增强体热膨胀系数差异造成的位错增殖形成的，可表示为[7]

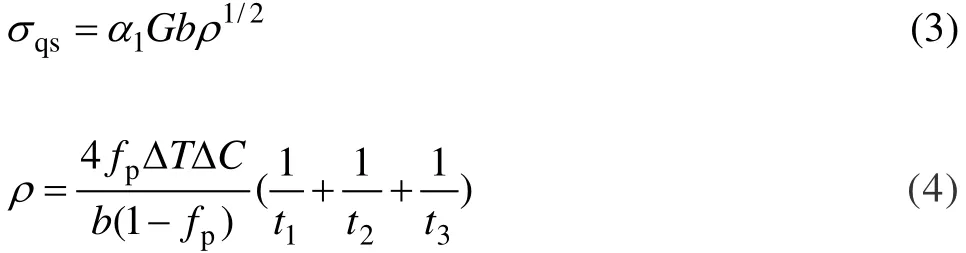
式中：ΔT是温度的变化；ΔC是基体与增强体的热膨胀系数差异；t1、t2和t3是增强体的三维参数；ρ是位错密度；α1=1.4是位错的强化系数。

晶粒细化强化效应(σgrs)来源于热加工过程中 SiC颗粒诱发再结晶引起的晶粒细化效应。假定每一个SiC颗粒可以诱发形成一个新的晶粒，则晶粒细化强化效应可表示为[8]

式中：Ky=0.1 MN·m−3/2为常数[15]。

几何必须位错强化效应(σgnds)来源于基体与增强体不同弹性模量，在变形过程中增强体的变形量比基体的变形量小，为保持变形的连续性以及避免产生孔洞，在基体中将产生位错来容纳基体与增强体的变形量差值。根据Ashby梯度应变理论[16]，几何必须位错强化效应可表示为

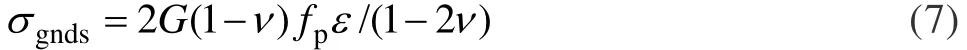
式中：ν是基体材料的泊松比；ε=0.002是复合材料的屈服应变。

1.2 考虑颗粒失效的修正剪切滞后模型

修正的剪切滞后模型没有考虑到SiC颗粒失效对复合材料屈服应力的影响。实际上，颗粒断裂和颗粒脱粘是复合材料在变形过程中存在的普遍现象[10−13,17]。由于失效的颗粒不再有承受载荷的能力，因此颗粒断裂与颗粒脱粘将不可避免地降低复合材料的屈服应力。早期的研究[17−18]表明，颗粒断裂的体积分数(fcr)和颗粒脱粘的体积分数(fde)均可以用 Weibull统计分布描述：

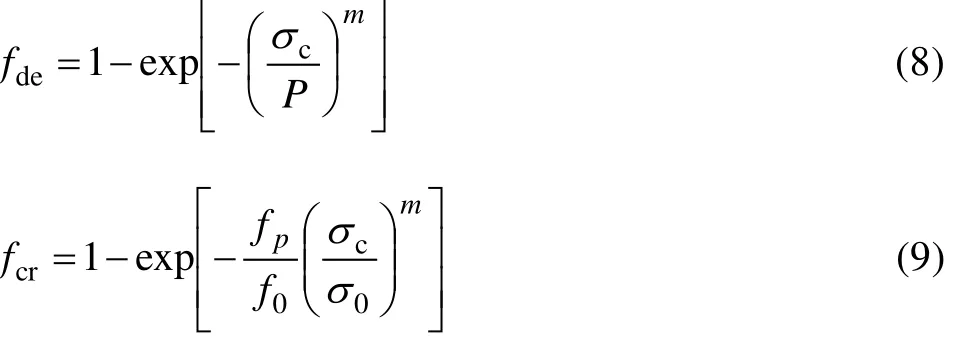
式中：σc为增强体所承受的应力；P是临界脱粘正应力函数；m为1~6是Weibull常数；σ0是SiC颗粒的断裂强度，f0为SiC颗粒在外加应力为σ0时的参考体积分数。LEE[19]的研究表明，临界脱粘正应力函数(P)可通过临界脱粘正应力(σd)和临界脱粘剪切应力(τd)计算：

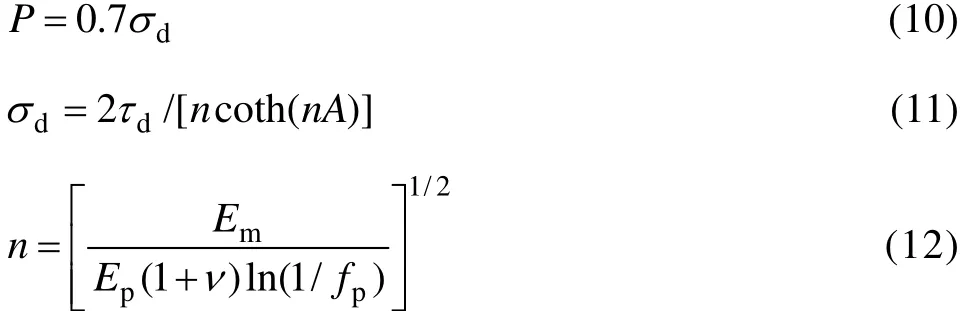
式中：Em和 Ep分别为基体和增强体的弹性模量。基于 Nardin-Schultz 模型[20]，临界脱粘剪切应力(τd)可表示为

式中：WA为基体与增强体界面的结合功函数；δ−1=0.5 nm为常数。

根据Weibull统计，计算SiC颗粒失效的体积分数需要知道 SiC颗粒承受载荷的大小(σc)。根据WITHERS等[14]的研究，SiC颗粒承受的载荷可以采用Eshelby 等效夹杂理论计算：

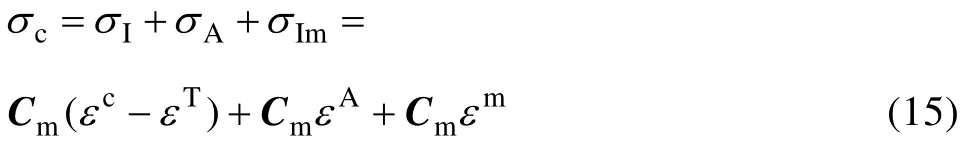
式中：σI、σA和σIM分别是Eshelby等效夹杂理论中由自由形状改变、外加应力和镜像力引起的附加应力；εA是在外力 σA作用下不含增强体的基体材料的塑性应变；εc、εm和εT是分别是约束应变、平均基体应变和等效转变应变；Cm是基体的弹性常数张量。对于大多数材料，由于存在对称性，为4阶张量的弹性常数可以约化为6×6的矩阵(不再是张量)。基于Withers等[14]的研究，约束应变(εc)、平均基体应变(εm)和等效转变应变(εT)可表示为式中：I 是单位矩阵；S为Eshelby张量；εT*是增强体的自由转变应变。由于断裂和脱粘的SiC颗粒不再具有载荷转移功能，因此，具有增强效应的有效 SiC颗粒的体积分数比实际SiC增强体的体积分数要小。结合颗粒脱粘和颗粒断裂的体积分数以及修正的剪切滞后模型，SiC增强铝基复合材料的屈服应力可表示为：

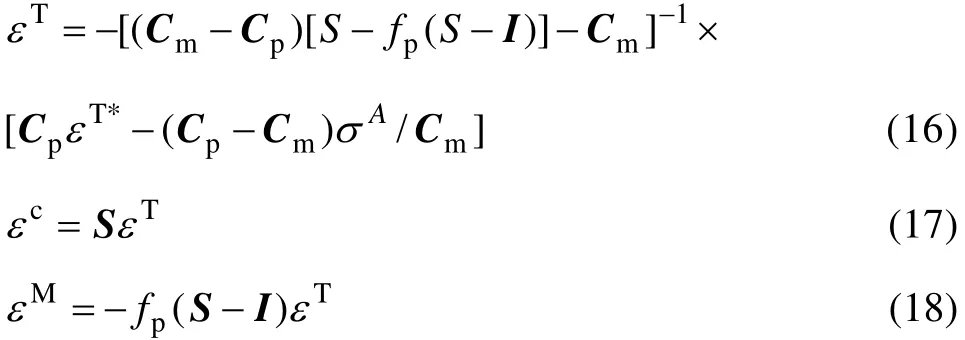
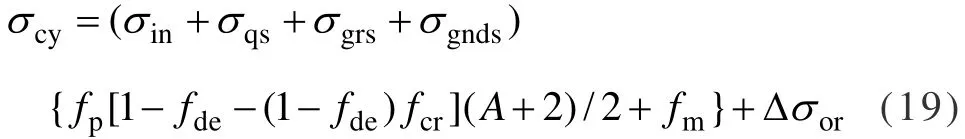
2 实验

实验中选择4种铝合金材料，包括纯度为99.7%的工业纯铝、Al-4.7%Mg-0.3%Si合金、Al-4.5%Cu-0.6%Mg合金和Al-6.4%Zn-2.3%Mg合金(质量分数)，作为基体材料来验证模型的准确性。复合材料采用粉末冶金法制备。首先采用雾化法制备铝合金粉，将铝合金粉与SiC粉混合搅拌后冷压成坯料，坯料经冷等静压后真空烧结，然后经挤压比为9的热挤压成棒材。挤压后的复合材料在420 ℃的温度下固溶10 h后水淬至室温。复合材料的屈服应力采用拉伸实验测试，试样的尺寸为 d5 mm×25 mm的标样，在 Instron 8802拉伸实验机上进行。所有试样均沿挤压方向，拉伸应变速率为 1×10−4s−1。

3 结果与讨论

采用本研究发展的力学模型计算SiC增强铝基复合材料的屈服应力需要知道基体材料的一些基本常数，如弹性模量、泊松比、基体材料的本征屈服应力，剪切模量及位错的泊氏矢量等。这些材料常数分别列于表1和2。

图1和2所示为模型计算以及实验所测得的4种不同基体材料的 SiC增强铝基复合材料屈服应力随SiC颗粒体积分数以及尺寸的变化。作为对比，修正剪切滞后模型的计算结果也包含在图中。从图1和2中可以看出，与传统的修正剪切滞后模型相比，本研究发展的模型计算的SiC增强铝基复合材料的屈服应力与实验结果吻合更好。传统修正剪切滞后模型预测的复合材料的屈服应力比本模型预测的复合材料的屈服应力要高，且屈服应力与SiC颗粒的尺寸无关，这与实验结果不相吻合。实际上，SiC增强铝基复合材料的屈服应力随着SiC颗粒体积分数的增加而增加，但随着SiC颗粒尺寸的增加而减小。复合材料屈服应力随SiC颗粒尺度的增加而减小的原因在于在相同的体积分数下，小尺度的SiC颗粒对应着小的颗粒间距，从而增大对位错的阻碍作用。

本研究发展的模型与传统修正剪切滞后模型的主要差别在于本模型考虑了SiC颗粒在变形过程中出现脱粘和断裂两种颗粒失效方式对复合材料屈服应力的影响。从载荷转移的角度出发，当一个增强体颗粒出现脱粘或断裂时，由于界面的出现导致应力集中而产生的应变能得到释放，从而使得颗粒失去强化效应。因此，采用传统修正剪切滞后模型计算的复合材料的屈服应力明显高于实验值，而本研究发展的模型由于考虑上述两种颗粒失效对复合材料屈服应力的影响，其计算结果与实验值吻合。

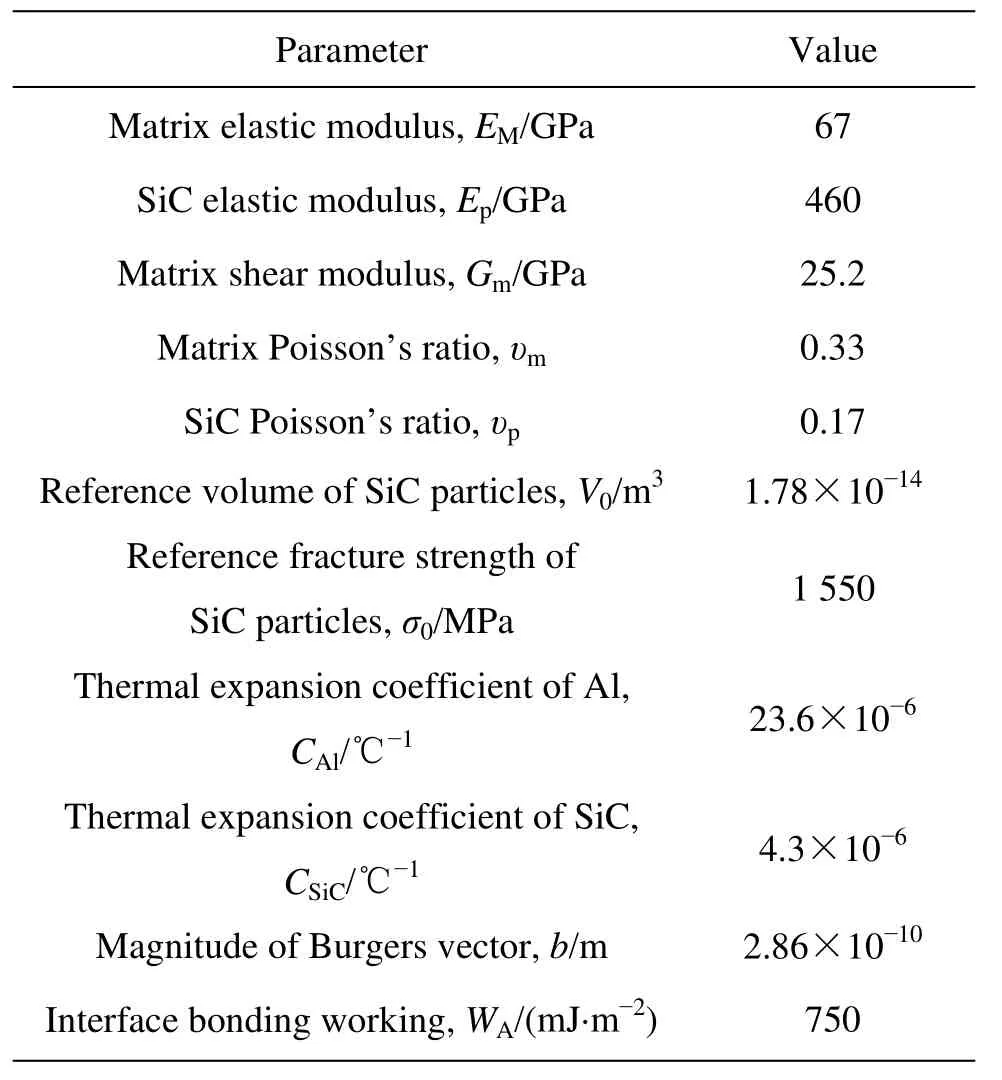
表1 计算所需的输入参数Table 1 Summary of input data in simulation

值得注意的是，复合材料的屈服应力不仅取决于增强体的尺度和体积分数，还取决于基体材料的种类。而基体材料对复合材料屈服应力的影响体现在如下两个方面：1) 基体材料的本征屈服应力；2) Weibull常数的值。从图1和2可以看出，高本征屈服应力的基体材料对应着高屈服应力的复合材料，同时还对应着较小的Weibull常数。一般来说，Weibull常数的值随着基体材料本征屈服应力的增加而减少，这表明较高强度的基体材料对应着较小的 Weibull常数。从统计学的角度出发，较低的 Weibull常数对应着较大的颗粒断裂和脱粘的几率，这表明高本征屈服应力的基体材料具有较高的颗粒失效分数。高本征屈服应力的基体材料具有较高的硬化行为，在变形过程中将更大的载荷转移到SiC增强体上，从而增加SiC颗粒失效的几率。从另一个角度来说，高本征屈服应力的基体材料由于具有较高的硬化行为，将在SiC颗粒与基体的界面附近产生更多位错，使得SiC颗粒有更高的应力集中，从而增加了SiC颗粒失效的几率。

4 结论

1) 基于修正的剪切滞后模型、Eshelby等效夹杂理论以及Weibull统计分布，发展了SiC增强铝基复合材料屈服应力的本构模型。模型考虑了变形过程中SiC颗粒失效(包括颗粒断裂和颗粒脱粘)对复合材料屈服应力的影响。

2) 选取工业纯铝、Al-Mg-Si, Al-Cu-Mg及Al-Zn-Mg 4种合金作为复合材料的基体材料，进行屈服应力的测试，对模型的准确性进行了验证。研究表明模型计算的复合材料屈服应力的演变规律与实验数据吻合很好，比传统的修正剪切滞后模型更加准确，表明 SiC颗粒失效对复合材料的屈服应力有重要的影响；

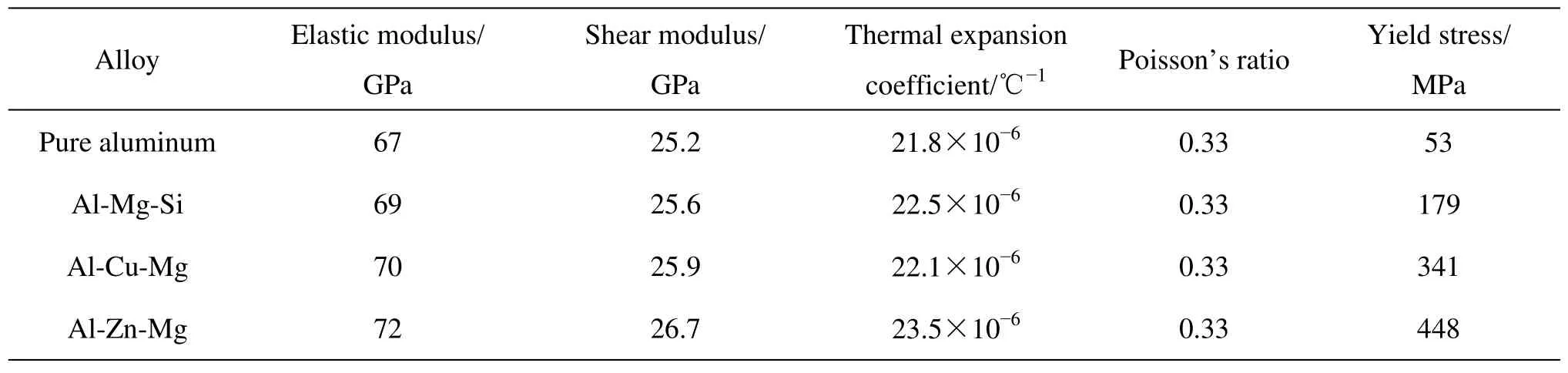
表2 计算所需基体材料的参数Table 2 Parameters of matrix alloys for tested composites in present work

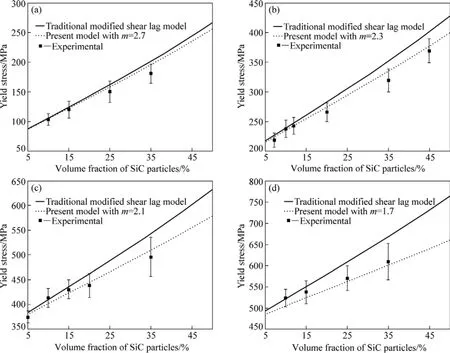
图1 计算及实验测得的SiC增强铝基复合材料的屈服应力随SiC颗粒体积分数的变化Fig.1 Changes of simulated and experimental yield stresses of SiC reinforced Al matrix composites with volume fraction of SiC particles (Size and aspect ratio of SiC particles are 20 µm and 1, respectively): (a) Pure aluminum; (b) Al-Mg-Si; (c) Al-Cu-Mg;(d) Al-Zn-Mg alloys

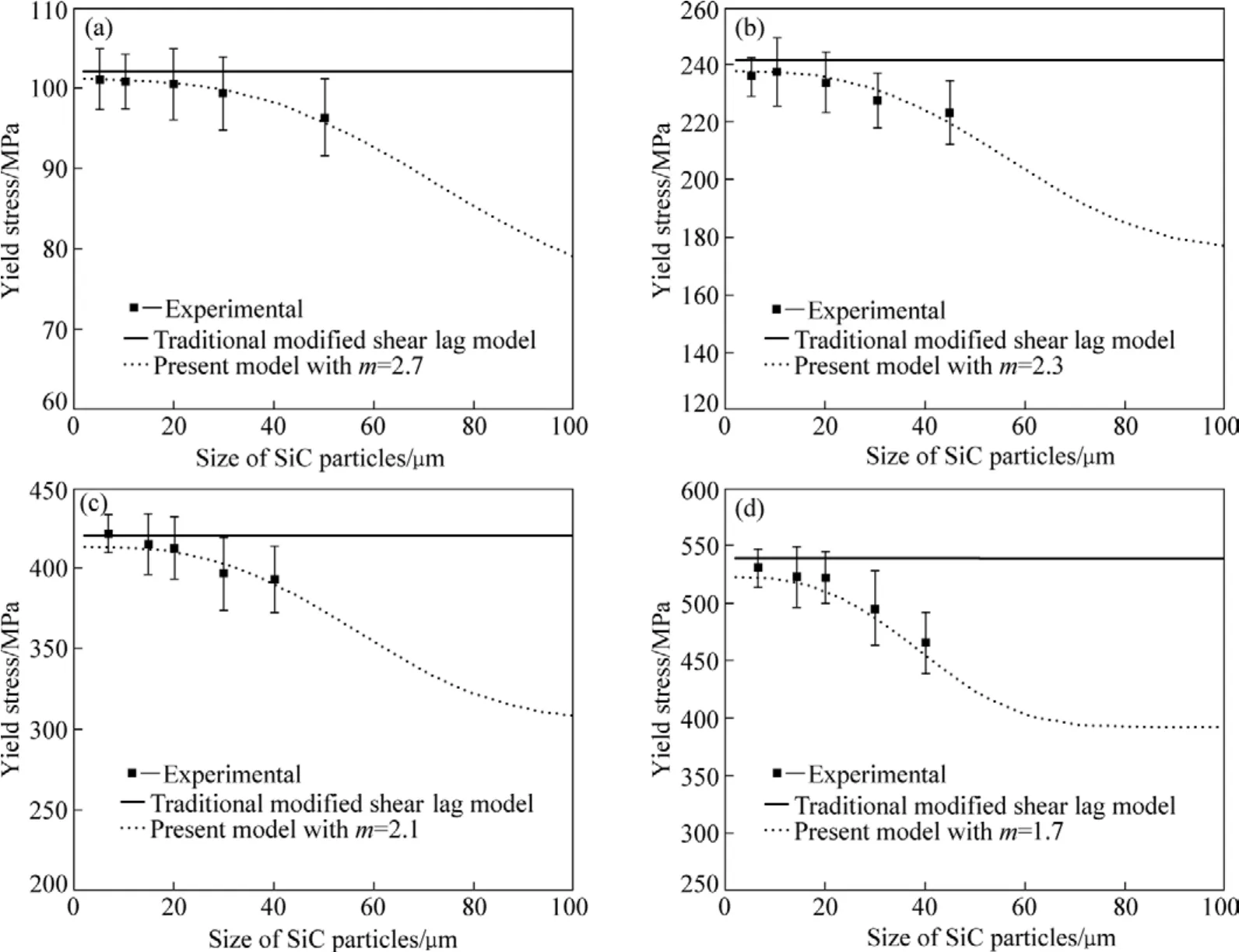
图2 计算及实验测得的SiC增强铝基复合材料的屈服应力随SiC颗粒尺寸的变化Fig.2 Changes of simulated and experimental yield stresses of SiC reinforced Al matrix composites with size of SiC particles(Volume fraction and aspect ratio of SiC particles are 10% and 1, respectively): (a) Pure aluminum; (b) Al-Mg-Si; (c) Al-Cu-Mg;(d) Al-Zn-Mg alloys

3) 复合材料的屈服应力随着 SiC颗粒体积分数的增加而增加，但随着SiC颗粒尺寸的增加而降低。复合材料的屈服应力不仅取决于增强体的尺度和体积分数，还取决于基体材料的种类。高本征屈服应力的基体材料对应着高屈服应力的复合材料，同时还对应着小的Weibull常数。

[1] COX H L. The elasticity and strength of paper and other fibrous materials[J]. Br J Appl Phys, 1952, 3(3): 72−79.

[2] 陈康华, 李 侠, 宋 旼, 黄大为. SiCp/Al合金复合材料时效强化的综合模型[J]. 金属学报, 2006, 42(8): 887−891.

CHEN Kang-hua, LI Xia, SONG Min, HUANG Da-wei. A combined model of the aging-strengthening of SiCp/Al alloy composite[J]. Acta Metallurgica Sinica, 2006, 42(8): 887−891.

[3] 宋 旼, 陈康华, 齐雄伟. 含有不同尺度微裂纹的铝合金伸长率模型[J]. 特种铸造与有色合金, 2007, 27(1): 3−6.

SONG Min, CHEN Kang-hua, QI Xiong-wei. A model for the tensile ductility of aluminum alloy with various-sized microcracks[J]. Special Casting & Nonferrous Alloys, 2007,27(1): 3−6.

[4] NARDONE V C, PREWO K M. On the strength of discontinuous silicon carbide reinforced aluminum composites[J].Scripta Metallurgica, 1986, 20(1): 43−48.

[5] 廖美春, 郭志昆, 陈万祥. 复合材料中纤维的抗拔机理[J]. 纤维复合材料, 2005, 3(1): 35−41.

LIAO Mei-Chun, GUO Zhi-kun, CHEN Wan-xiang. Study on Anti-Tensile Mechanism of Fiber in Composites[J]. Fiber Composites, 2005, 3(1): 35−41.

[6] SONG M, HUANG D. Experimental and modeling of the coupled influences of variously sized particles on the tensile ductility of SiCp/Al metal matrix composites[J]. Metallurgical and Materials Transactions A, 2007, 38(9): 2127−2137.

[7] SONG M, CHEN K H, QI X W, HUANG L P. A multi-scaled model for the fracture toughness of an aluminum alloy[J]. J Mater Sci, 2007, 42(12): 4177−4282.

[8] MILLE W S, HUMPHREYS F J. Strengthening mechanisms in particulate metal matrix composites[J]. Scripta Metall Mater,1991, 25(1): 33−38.

[9] SONG M, LI X, CHEN K H. Modeling the ageing hardening behavior of SiC/Al metal matrix composites[J]. Metall Mater Trans A, 2007, 38(3): 638−648.

[10] SONG M, XIAO D. Modeling the fracture toughness and tensile ductility of SiCp/Al metal matrix composites[J]. Mater Sci Eng A,2008, 474(1/2): 371−375.

[11] 宋 旼, 袁铁锤, 张福勤, 黄伯云, 陈康华. Al-Cu-Mg合金的断裂韧性及拉伸延性模拟[J]. 中国有色金属学报, 2007, 17(7):1034−1040.

SONG Min, YUAN Tie-chui, ZHANG Fu-qin, HUANG Bai-yun, CHEN Kang-hua. Modeling on fracture toughness and tensile ductility of Al-Cu-Mg alloy[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(7): 1034−1040.

[12] 陈康华, 方 玲, 李 侠, 黄大为, 方华婵. 颗粒失效对SiCp/Al复合材料强度的影响[J]. 中南大学学报: 自然科学版,2008, 39(3): 493−499.

CHEN Kang-hua, FANG Ling, LI Xia, HUANG Da-wei, FANG Hua-chan. Influence of particle failure on strength of SiCp/Al composites[J]. Journal of Central South University: Science and Technology, 2008, 39(3): 493−499.

[13] MAIRE E, WILKINSON D S, EMBURY J D, FOUGERES R.Role of damage on the flow and fracture of particulate reinforced alloys and metal matrix composites[J]. Acta Materialia, 1997,45(12): 5261−5274.

[14] WITHERS P J, STOBBS W M, PEDERSEN O B. The application of the Eshelby method of internal stress determination to short fiber metal matrix composites[J]. Acta Metall, 1989, 37(11): 3061−3084.

[15] SEKINE H, CHEN R. A combined microstructure strengthening analysis of SiCp/Al metal matrix composites[J]. Composites,1995, 26(2): 183−188.

[16] LIU G, SUN J, NAN C W, CHEN K H. Experiment and multiscale modeling of the coupled influence of constituents and precipitates on the ductile fracture of heat-treatable aluminum alloys[J]. Acta Mater, 2005, 53(10): 3459−3468.

[17] LEWIS C A, WITHERS P J. Weibull modeling of particle cracking in metal matrix composites[J]. Acta Metall Mater, 1995,43(10): 3685−3699.

[18] 李 侠, 陈康华, 黄大为. 增强颗粒对颗粒增强铝基复合材料强度的影响[J]. 铝加工, 2006, 167(2): 9−13.

LI Xia, CHEN Kang-hua, HUANG Da-wei. Influence of reinforced particle on strength of particle-reinforced aluminum matrix composites[J]. Aluminum Fabrication, 2006, 167(2):9−13.

[19] LEE H K. A computational approach to the investigation of impact damage evolution in discontinuously reinforced fiber composites[J]. Comp Mech, 2001, 27(6): 504−512.

[20] SHIMBO M, NAKA M, OKAMOTO I. Wettability of silicon carbide by aluminum, copper and silver[J]. J Mater Sci Lett,1989, 8(6): 663−666.