加权微粒群算法在模型配准中的应用
刘 晶, 林大钧
(华东理工大学机械与动力工程学院,上海 200237)
微粒群算法[1]是在1995年由美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出的,其基本思想是受他们早期对鸟类群体行为研究结果的启发,并利用了生物学家Frank Heppner的生物群体模型[2]。目前微粒群算法应用范围较广,已经在函数优化,多目标优化,人工神经网络,模式识别等领域得到应用[3]。基本微粒群算法由于收敛性能还有待优化,本文利用加权函数以及分群搜索来对基本微粒群算法进行改进。
1 基本微粒群算法
很多进化算法对于个体使用进化算子,基本微粒群算法与这些进化算法的不同之处在于,它是将每个个体看作是在n维搜索空间中的一个没有重量和体积的微粒,并在搜索空间中以一定的速度飞行。该飞行速度由个体的飞行经验和群体的飞行经验进行动态调整[2]。设第i个微粒的当前位置表示为xi=(xi1, xi2, …, xin),微粒i的当前飞行速度表示为vi=(vi1, vi2, …, vin),微粒i经历过的最好位置表示为pi=(pi1, pi2, …, pin),设群体中微粒个数为m,所有微粒经历的最好位置用pg来表示。则微粒群算法的进化方程如下

其中 参数t表示第t代,c1, c2为加速常数,c1用于调节微粒飞向自身最好位置方向的步长,c2用于调节微粒向全局最好位置飞行的步长。r1, r2为位于0与1之间的随机函数。vi通常介于[-vmax, vmax]之间。公式(1)中第一部分是微粒上一代的速度,第二部分是认知部分,表示微粒自身的思考,第三部分是社会部分,表示微粒间的社会信息共享。第一部分用于保证算法的全局收敛性,第二部分和第三部分保证算法具有局部收敛能力[2]。 基本微粒群算法的进化过程中,只有当微粒的当前位置处的适应值好于所经历的最好位置处的适应值时,就用微粒的当前位置替换微粒所经历的最好位置。迭代中止条件可以通过最大迭代数或者最小适应阈值来控制。但是,基本微粒群算法的收敛性还有待完善,因此需要引入权函数。
2 加权微粒群算法
为了改善基本微粒群算法的收敛性能,加权微粒群算法在速度进化过程中引入权函数,同时在迭代一定次数后进行分群优化。
因此引入权函数后公式(1)改进如下

文献[4]建议w 的取值范围为[0,1.4],但实验结果表明当w 取[0.8,1.2]时,算法收敛速度更快,而当w>1.2 时,算法则较多地陷入局部极值[2]。因此,本文建立的权函数使之范围在[0.8,1.2]这个范围。由于较大的w 具有较好的全局收敛能力,而较小的w 具有较好的局部收敛能力。因此,在迭代初期应使得w 大些,在迭代后期应使得w小些。从而使得微粒群算法在迭代初期具有较好的全局收敛能力,而在迭代后期具有较好的局部收敛能力。因此,建立权函数公式如下
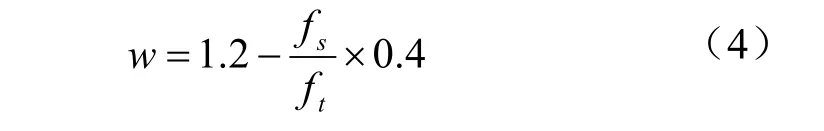
其中 fs表示最小适应阈值,ft表示第t代最好位置处的适应值。
当微粒群迭代了一定次数时,就可以进行分群,将微粒群分为两个子群。分群的目的是提高多样性和扩大搜索范围,避免找到局部最优。分群的原则是:根据各个微粒的最优适应值,将其按从小到大排序,然后把位于奇数位置的微粒放到一个群,把位于偶数位置的微粒放到一个群。分群后每个微粒所经历过的最好位置作为它在分群中的初始位置,以便后续过程能快速找到最优解。
本文采用的加权微粒群算法的基本流程如下:
Step 1 随机初始化微粒的速度和位置。
Step 2 计算每个微粒的适应值,微粒i经历过的最好位置表示为pi, pg设置为全局所经历的最好位置。
Step 3 对于每个微粒,将其适应值与所经历过的最好位置pi的适应值进行比较,若好于所经历过的最好位置pi处的适应值,则将其作为当前的最好位置。
Step 4 对每个微粒,将其适应值与全局所经历的最好位置pg的适应值进行比较,若好于全局最好位置pg处的适应值,则将其作为当前的全局最好位置。
Step 5 根据公式(3)和公式(2)对微粒的速度和位置进行进化,再执行Step 3和Step 4。
Step 6 当迭代一定次数时,进行分群,将目前的这群微粒分为两个分群,由于已经进行一定次数的迭代,因此每个微粒所经历过的最好位置作为它在分群中的初始位置,从而保证分群中的初始位置都是比较好的位置。
Step 7 将两个分群分别按照Step 5进行优化,如适应值小于设定好的适应阈值则结束,从而分别得到各自的最优值,将两个分群的最优值进行比较,其中较好的值作为最终的最优值。
3 实例分析
本文利用上文提到的加权微粒群算法对三坐标机测量的叶片散乱点云到其三维CAD 模型的配准问题进行研究。散乱点云与三维CAD 模型的配准其实质就是使散乱点云到三维CAD 模型的距离平方和最小。因此,加权微粒群算法中每个微粒的适应值就是该微粒条件下散乱点云到三维CAD 模型的最小距离平方和。适应值公式如下

其中 Ai(i=1, 2, …, L)表示散乱点云中的数据点,Bi为Ai在CAD 模型上的投影点,R 为旋转矩阵,T 为平移矩阵,L 为散乱点云的数目。R可以表达成下式

其中 3 个参数α, β, γ 分别表示围绕X,Y,Z三个坐标轴的旋转角度。
T 可以表达成下式
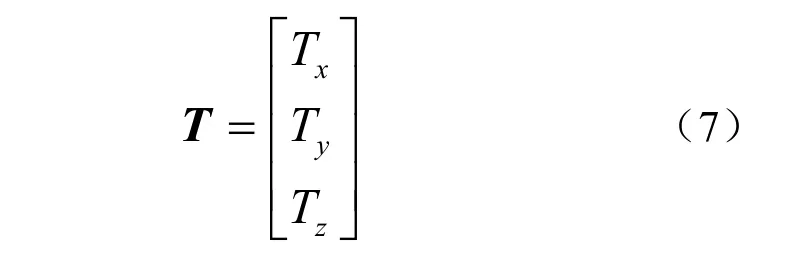
其中 3个参数Tx, Ty, Tz分别表示沿X,Y,Z方向的位移量。
因此,从公式(5)中可以看出适应值是一个包含了6个参数的函数。从而可以确定加权微粒群算法的搜索空间为6维,以α, β, γ,Tx, Ty, Tz这6个参数可以确定出微粒的位置。只要按照第三部分叙述的加权微粒群算法的基本流程,当适应值小于设定好的适应阈值时,就可以确定出全局最好位置,也就是确定出R 和T 最佳变换的6个参数,从而实现配准。
取群体微粒数为20, w按公式(4)获得,c1= c2= 2 , vmax= 4。散乱点云数目为224,设定适应阈值为0.1,分别利用基本微粒群算法和加权微粒群算法对散乱点云与三维CAD模型的配准问题进行研究,结果如表1所示。如果想提高配准精度,可以修改中止条件,使适应阈值更小。

表 1 运算结果
普通微粒群算法以及加权微粒群算法的适应值迭代过程以及配准后平均误差的迭代过程如图1 和图2 所示。
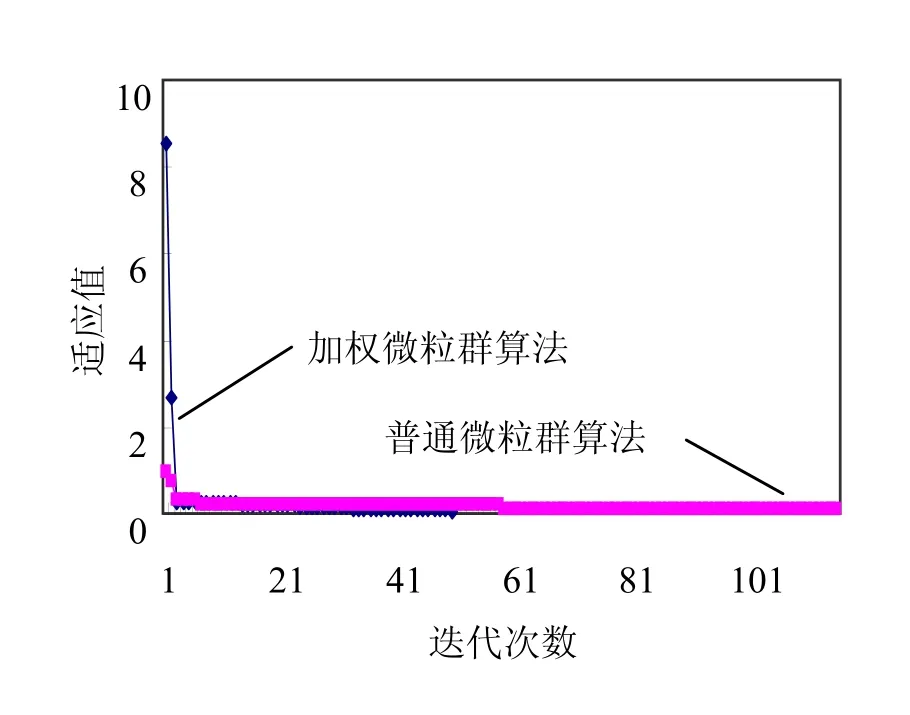
图1 适应值迭代图
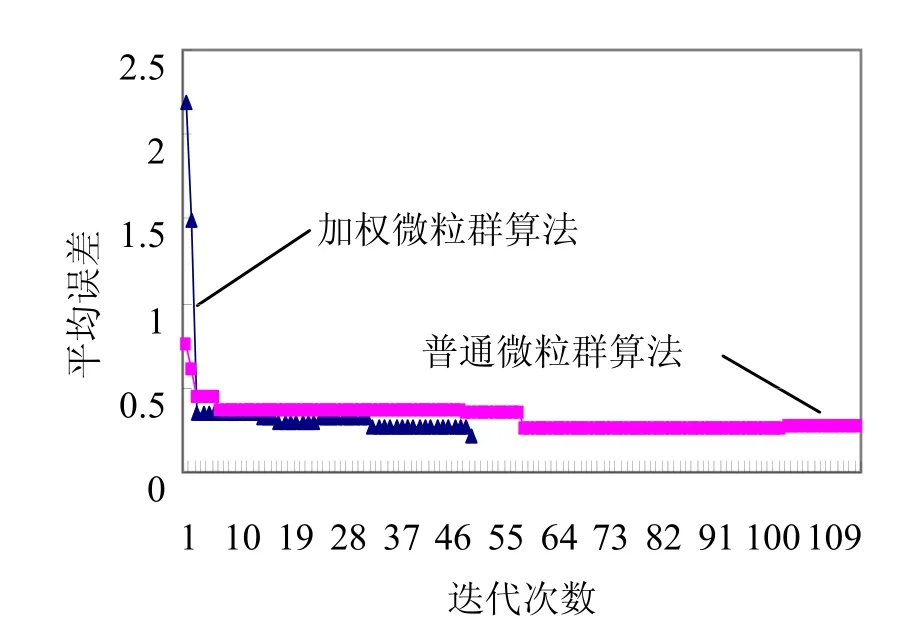
图2 平均误差迭代图
4 结 论
本文把加权微粒群算法运用到散乱点云与CAD 模型间的配准。根据算法收敛较快的权值范围,建立加权函数并将其引入速度进化过程中,同时在进化过程中分群优化,从而维护全局和局部搜索能力的平衡。进而更好地实现了散乱点云与三维CAD 模型之间的配准。
[1] Kennedy J, Eberhart R C. Particle swarm optimization [C]// Proc. of IEEE Int. Conf. on Neural Networks. Perth, WA, Australia, 1995: 1942-1948.
[2] 曾建潮. 微粒群算法[M]. 北京: 科学出版社, 2004. 7.
[3] 谢晓锋, 张文俊, 杨之廉. 微粒群算法综述[J]. 控制与决策, 2003, 18(2): 129-134.
[4] Shi Y, Eberhart R C. Parameter selection in particle swarm optimization [C]//Evolutionary Programming VII: Proc. EP98. New York: Springer-Verlag, 1998: 591-600.

