确定任意形状物体最小包围盒的一种方法

陈 华

（西安理工大学理学院，陕西 西安 710048）

物体的包围盒广泛应用于碰撞检测、模具分型设计、产品包装设计以及图像处理、模式识别等领域。包围盒的基本思想是利用某种形状简单的几何体来紧密包裹对象物体。常见的包围盒类型主要有正六面体（长方体）和球体等。一般来说，由于包围球的紧密性不够好，因此在应用中多采用长方体包围盒。根据该包围盒的3个边与坐标轴的位置关系，长方体包围盒主要分为沿坐标轴的轴向包围盒AABB(Axis-Aligned Bounding Boxes)和任意方向的方向包围盒OBB (Oriented Bounding Box) 及其它改进形式[1-2]。AABB的确定相对而言比较简单，在现有的CAD软件中就能直接得到结果，但由于它是平行于坐标轴的定方向的包围盒，所以不能保证是最小的包围盒。而OBB最大的特点是其方向的任意性，这使得它可以根据被包围对象的形状特点尽可能紧密地包围对象，从而做到使包围盒的体积最小。由于OBB的这一优点，近年来在其生成方法研究，特别是在碰撞检测中的应用方面研究较多。文献[3]提出了一种多面体模型的最小体积的包围盒生成算法，用以确定模具的分型方向；文献[4]将包围盒技术应用于三维模型的数据点配准，以扫描数据生成的三角网格模型为对象，应用单纯形优化算法生成三维模型的最小包围盒，进而实现数据点配准；文献[5]研究了层次OBB在5轴数控加工中的应用，提出了刀具OBB与工件八叉树的干涉检测方法。

上述文献表明，OBB的应用范围相当广泛，但是由于问题的复杂性和目标对象形状的任意性，目前的文献主要是针对平面立体或用三角形面片形式表示的物体，其算法相对都比较复杂，计算量随物体顶点数或三角面片个数的增加而急剧增加。本文提出了一种简单、实用的确定任意物体最小包围盒的方法，利用现有的CAD软件本身具有确定AABB的功能，通过对CAD软件的二次开发，利用程序自动确定出任意形状物体的最小包围盒。

图 1 物体旋转前后的AABB

1 算法思路

1.1 AABB 与OBB

AABB是平行于坐标轴的定方向的最小长方体包围盒，其体积大小和3个边长除了与物体本身的形状和大小有关，还与物体相对于坐标系的角度有关。一个物体在坐标系中的方向确定后，就对应唯一的AABB，在现有的CAD软件中能直接得到其结果。但是，由于AABB与物体相对于坐标系的角度有关，某一方向下得出的AABB不能保证是物体最小的长方体包围盒。为了得到最小包围盒，可以设想将物体在坐标系中分别绕X、Y、Z轴旋转，每旋转一个位置，求出其AABB，这些AABB中至少有一个是最小包围盒。

方向包围盒OBB的3个边长大小只与物体的形状和大小有关，与其在坐标系的摆放角度无关。在一个确定的坐标系中，物体的OBB三个边相对于坐标系有特定的角度，换句话说，如果将原坐标系旋转该角度，那么原坐标系中的OBB也就是旋转变换后新坐标系中的AABB。由此可以设想，不断地旋转坐标系并求在该坐标系中的AABB，也能得到物体的最小包围盒，即在原坐标系下的OBB。图1给出了物体旋转前后在同一坐标系下不同的AABB，图2则是物体不动坐标系旋转变换前后在两个坐标系下的AABB。

图 2 坐标系旋转前后的AABB

1.2 算法思路

要利用绘图软件提取实体在任意方向下的包围盒，有两种途径，一种是将物体作旋转变换，一种是将坐标系作旋转变换。两种方法得到的包围盒大小是一样的。相对而言，坐标系旋转比物体旋转要简单得多，在旋转n3次的情况下，利用后一种途径，运算速度会大大提高。

图3是本文方法的程序框图。程序首先进行初始化，设3个坐标轴的转角α、β、γ分别为0，并建立一个空文件，用以保存结果数据，然后选择对象，按一定的角度步长，用三重循环分别使3个坐标轴进行0°～360°的旋转。在每个旋转位置，提取对象的物性参数，从中得到包围盒的边界数据{Xi}和体积Vi，其中{Xi}＝{Xmin，Xmax，Ymin，Ymax，Zmin，Zmax}。比较每个位置的包围盒体积，可得出最小包围盒及其对应的转角α0、β0、γ0，保存在程序开始所建立的文件中。由α0、β0、γ0可直接得出包围盒的3个边长相对于初始坐标系的夹角，从而确定出对象的OBB。

在该方法中只要改变比较条件，就可求出满足不同要求的最小包围盒，如最小表面积的包围盒（产品的包装盒生产时）、某一边长最大/最小的包围盒（模具分型方向确定）等。

2 应用举例

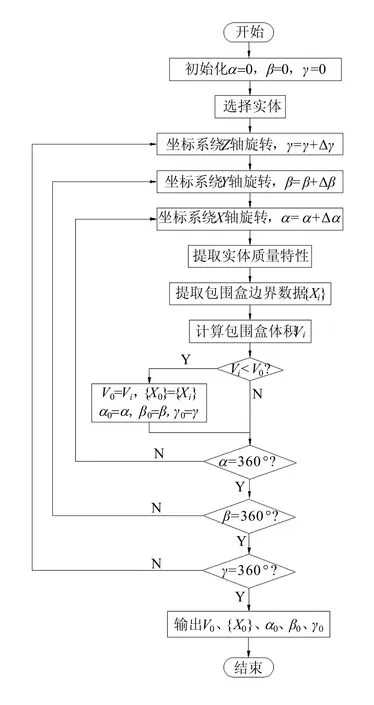
图 3 程序框图

上述算法可以在任何具有物性提取功能的三维CAD软件中实现。这里以国内外广泛使用的AutoCAD软件为平台，采用嵌套在其内部的AutoLisp语言编程予以实现。程序的核心是 AutoCAD的“MASSPROP”命令和“UCS”命令的调用。使用“MASSPROP”命令将生成一个物性文件，存储对象的体积、质心坐标、AABB的3个边长边界坐标、对象的惯性矩、惯性积等物性数据。而“UCS”命令则用以新建一个坐标系，有多种创建方法。本文利用的是绕原坐标系的某个轴旋转一定角度，建立新坐标系的方法，在具体编程时，调用“MASSPROP”命令的语句放在三重循环的最内层，而三重循环的每一层均要调用“UCS”命令，分别实现使坐标系绕X、Y、Z旋转。

图4 是某物体的三维模型，物体体积为2526148mm3，表面积为114273mm2。在初始位置下的AABB包围盒的体积是10369845mm3，平行于X、Y、Z轴的3个边长分别是182.618mm，198.512mm，286.050mm。

利用本文所编制的程序，确定出其最小体积包围盒的体积是7121911mm3，3个边长分别是307.790 mm，180.271mm，128.356mm，包围盒表面积是236262 mm2，它是将原坐标系分别绕X轴旋转α=144°、绕Y轴旋转β=72°、绕Z轴旋转γ=18°建立的新坐标系下的AABB，也就是物体在原坐标系下的OBB，如图5所示。如果追求包围盒表面积最小，则可得出最小表面积的包围盒体积为7121956mm3，包围盒表面积是235926 mm2，3 个边长分别是305.776mm，180.754mm，128.857mm，此结果是将原坐标系分别绕X轴旋转α=126°、绕Y轴旋转β=72°、绕Z轴旋转γ=36°得出的。不同的包围盒的参数对比如表1所示。由此可见，最小体积的包围盒与最小表面积的包围盒有可能是不同的，对于不同的应用场合，应根据需要确定合适的包围盒类型，再确定包围盒的参数。

图 4 物体模型及其AABB

图 5 物体的最小体积包围盒

表 1 同一物体不同要求包围盒的参数对比

3 结 论

对物体包围盒的研究目前主要集中于虚拟现实技术中的碰撞检测方面，在企业生产中的模具分型设计和产品包装设计等方面也有一定应用。方向包围盒OBB由于其对物体的包裹紧密性强的特点，是目前应用最多的一种包围盒。但现有文献中OBB的确定主要是针对平面立体或用三角形面片形式表示的物体，其计算量随物体顶点数或三角面片个数的增加而急剧增加。本文提出的确定任意形状物体最小包围盒的方法，基于现有软件确定AABB的功能，通过二次开发，可自动确定出任意形状物体的最小体积包围盒或最小表面积包围盒。这种确定OBB的方法只要求有物体的三维实体模型，对其形状没有限制，也不需要复杂的计算，因而简单、实用，具有广阔的应用前景。

[1] 马登武, 叶 文, 李 瑛. 基于包围盒的碰撞检测算法综述[J]. 系统仿真学报, 2006, 18(4)： 1058-1061.

[2] 谭同德, 吴 强, 赵红领, 等. OBB层次包围盒构造方法的改进[J]. 计算机工程与应用, 2008, 44(5)： 79-81.

[3] 郭九生, 初红艳, 卢秉恒. 多面体最小体积的包围盒生成算法研究[J]. 计算机应用, 2001, 21(1)： 38-40.

[4] 张开兴, 张树生, 白晓亮. 基于最小包围盒的三维模型的配准技术[J]. 机床与液压, 2008, 36(4)： 5-7.

[5] Ding S, Mannan M A, Poo A N. Oriented bounding box and octree based global interference detection in 5-axis machining of free-form surfaces [J]. Computer-Aided Design, 2004, 36(13)： 1281-1294.