斜对称面检测在二次曲面体中的应用

王 翔， 丁运亮， 李 静

（1. 南京航空航天大学航空宇航学院，江苏 南京 210016； 2. 南京航空航天大学自动化学院，江苏 南京 210016）

在从二维投影还原三维实体的过程中存在许多重要的几何特征约束，对称就是其中的一 个[1]。对称将三维的自由度降低到二维；可以避免重复约束，因而大大降低了三维重建的难度，此外，对称还可以克服图素间的遮挡和互叠问题，即可以通过寻找对称面来恢复被遮挡部分的实体。因此，对称问题具有很高的研究价值。

当观察者从非投影方向观察对称时，便产生了斜对称，图1 中就是几个斜对称的例子，由于大多数情况下（除正投影外）视角均同投影方向有一定的夹角，因而斜对称是普遍存在的。由于斜对称是三维世界中的真实对称在二维情况下的反映，这就将三维中对称检测转化成了二维图形下的斜对称检测。

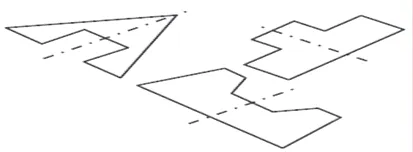
图1 斜对称示例

在斜对称检测方面，许多人进行了大量的研究。Oh[2]和Yip[3]采用Hough 变换的方法进行斜对称检测，该方法能够在干扰点存在以及图形封闭的情况下进行点和曲线的对称检测，算法繁琐。Shen[4]采用仿射不变特征向量法，通过一组仿射不变特征向量来描述图形的几何边界，最终归结为通过求解相似矩阵来寻找线段（对称轴）的问题。算法复杂度为O(n2)，其中n 是为计算面积而在边界上取的特征点数。算法效率有很大提高但是仅限于二维。Yip[5]采用椭圆傅立叶变换描述符对平行投影下的斜对称进行检测。该算法对于几何实体的投影方向要求过于严苛，且不允许有遮挡情况存在。Lipson 和Shpitalni 提出了一种简便有效的检测方法，通过计算最大权值系数来寻找对称轴，该算法仍然只适用于2D，无法检测3D 的斜对称面。

Zabrodsky[6]将对称距离引入到了对称检测中，其将对称距离定义为把某一实体变换到对称位置所需移动的最小距离，其计算方法是取原物体所有的特征点在对称变换中移动距离的平方的均值，理论上该方法能够解决3D 空间中的对称检测问题，但是庞大的计算量使其无法处理复杂的模型。

Sugimoto[7]提出了自底向上的对称检测方法，通过对低维图素包括直线和曲线的斜对称轴检测来实现高维图形的斜对称检测，该算法能够处理图素的遮挡和隐藏情况。但是，在曲线检测部分只给出了椭圆的斜对称轴检测方法，在此基础上，本文将其扩展并给出了任意二次曲线的斜对称轴检测方法。

在三维实体斜对称面检测方面，Zou[8]从点线面的拓扑关系入手，提出了平面体的斜对称面检测方法，但算法覆盖域仅限于平面体，无法处理二次曲面体。之所以二次曲面体的斜对称检测最为复杂，是因为三维空间对称面检测归根到底还是通过平面内的斜对称轴检测来实现的，以往的平面斜对称轴检测算法最多给出了椭圆线的检测，而对于像双曲线、抛物线等复杂的二次曲线则没有相应的检测方法。这样，对于圆柱面等投影为圆或椭圆的规则曲面体，且放置位置固定时，可以用以往的算法加以解决，而对于其他二次曲面体或特殊摆放位置的实体以往算法则不能给出解决的方案。

本文从任意放置的空间二次曲线重建入手，通过计算曲线的参数表示来实现对曲线的类型辨识，再通过扩展改进的斜对称轴检测算法对所有面域图素进行斜对称轴检测，最后剔除对称面内曲线得到对称面多边形的边界，组装成面即可得到二次曲面体的斜对称面。

1 面域提取

斜对称检测是在独立的图素（直线或二次曲线）中进行的，所以要将整个模型分割成独立的面域。在这一步中需要输入的是二维顶点的坐标，输出为一系列独立的平面或曲面方程，生成的是平面或是曲面则由以下3 种情况决定[9]：

（1） 两条不共线的直线边决定一个平面；

（2） 一条直线边和一条二次曲线边相交，若直线边位于曲线边的支撑平面内，则两边确定一个平面，否则对应生成一个二次曲面；

（3） 两条二次曲线边相交，若两曲线边的支撑平面重合，则两边确定一个平面；否则对应生成一个二次曲面。

使用极左邻边搜索法[10]即可提取所有表面上的闭环，根据相互间的位置关系如包含或分离确定内环或外环。所有外环和内环间的部分即构成一个面域（见图2）。

图2 面域分割

2 预处理

提取得到的面域是一个个独立的、闭合的多边形，无法直接对其进行对称检测，因此首先要进行一些预处理工作，其中主要包括图形的分 割[11]和曲线的参数表达式求解。图形经分割后得到的图素包括线段和曲线是斜对称轴检测算法的直接作用对象，被打断的图素只是在连接关系上发生了改变，而其坐标位置和几何拓扑关系并未改变。不同的曲线类型对应的检测算法也不相同，因此在检测前要对得到的曲线进行类别辨识，本文则是通过求解曲线的几何参数表达式来确定曲线的类型。

2.1 图形分割

将第一步提取的面域进行分割处理，分割位置为轮廓线段的交点、端点以及曲线的极值点和拐点。相应的判定方法是：交点处线段的连接度大于2；端点处的曲率有急剧的变化；极值点处曲率正负发生改变；拐点则是曲率从零值变为非零值。

分割后的图素经过曲率检验后被分为直线和曲线两大类。而经过下一步的曲线参数表达式求解之后，曲线将进一步被划分为椭圆、双曲线和抛物线等。

2.2 投影曲线参数表达式求解

在计算机的几何实体表示方法中，二次曲线在二维坐标下一般有参数表达和隐式表达两种表达方法。因参数表达法具有直观简洁的特点，故通常采用更多的是这种表达方法，参数表达法首先需要明确二次曲线的类型，然而在三维重建的问题描述中，投影视图中的曲线类型是未知量，并且很难用模式识别的方法获得其几何参数。基于以上考虑，本文首先采用“五点法”[10]从视图投影曲线直接构造其一般代数表达式，然后采用解析法将得到的代数表达式转换成相应类型的几何参数表达式，为下一步的斜对称轴检测做准备。

2.2.1 “五点法”构造投影曲线代数表达式

平面二次曲线的一般代数表达式为

根据定理“给定五点，其中任意三点不共线，那么可以唯一确定一条二次曲线。”在投影曲线 上任意选取满足要求的 5 个点 Pi( xi, yi) ( i= 1,2,… , 5)，则曲线的代数方程（1）的系数 可以通过求解方程组

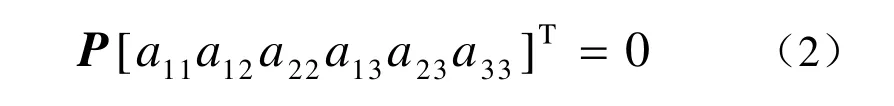
确定。其中

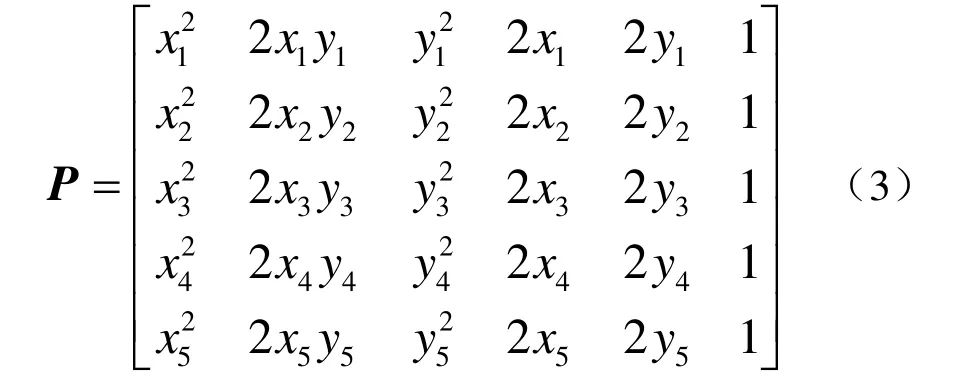
令点对 ( pv1, pv2)、( ph1, ph2)、( pw1, pw2)分别表示主、俯、侧视图中的两投影节点，以S ( pv1, pv2)、 S ( ph1, ph2)、 S ( pw1, pw2)分别表 示各视图中的两投影节点间存在的连接线段。这 样，应用“五点法”，分别由点 pvi∈S ( pv1, pv2)、 phi∈S ( ph1, ph2)、pwi∈S ( pw1, pw2) ( i= 1,2,… , 5)可构造出相应的连接线段S ( pv1, pv2)、 S ( ph1, ph2)、 S ( pw1, pw2)的代数 表达式。

2.2.2 参数表示转换

转换后得到的曲线参数：

（1） 曲线的方向角θ

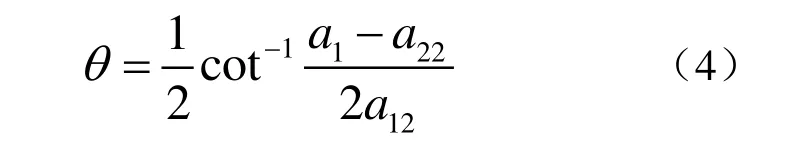
（2） 中心型二次曲线（椭圆、双曲线）的中心 ( x0, y0)

（3） 中心型二次曲线的长短轴 },{ ba 椭圆

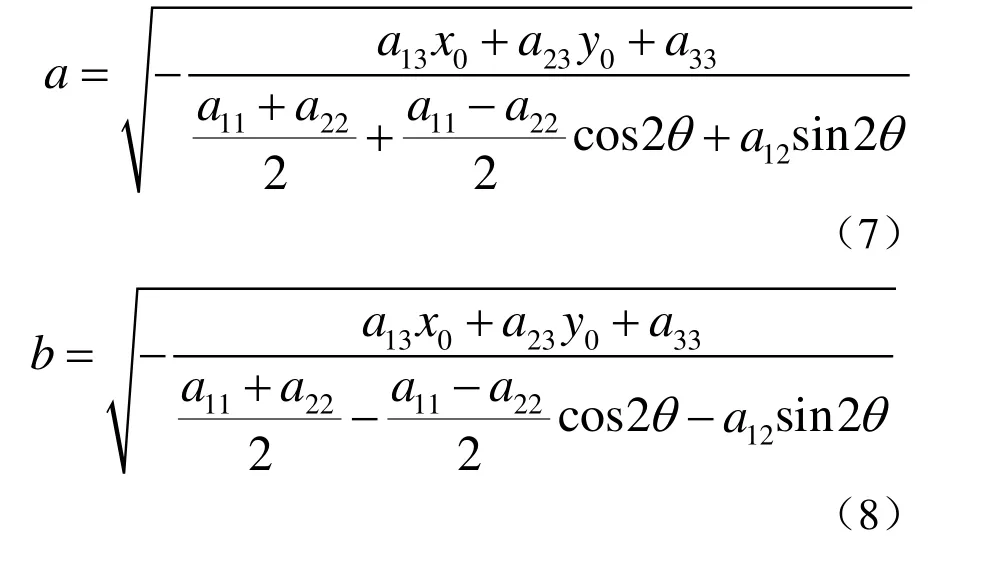
双曲线

（4） 无心二次曲线（抛物线）的焦距和顶点坐标

焦距

所有数据采用SPSS 24.0统计软件进行处理，所有检验均为双侧检验，P＜0.05表示差异有统计学意义。计量资料采用（±s）进行统计描述，两组间比较采用独立样本t检验，方差不齐，采用t＇检验，多组间比较采用单因素方差分析（F检验）。计数资料采用率和频数进行统计描述，率的比较采用χ2检验。尿酸与血压、血糖等指标的相关分析采用简单相关分析，因各指标之间也相互关联，为排除各因素之间的影响，故将尿酸与各指标在简单相关分析后再控制其他因素进行偏相关分析，如尿酸和身体质量指数进行偏相关分析时，控制因素为收缩压、舒张压、空腹血糖、甘油三酯、总胆固醇、高密度脂蛋白胆固醇、低密度脂蛋白胆固醇，依此类推。

其中

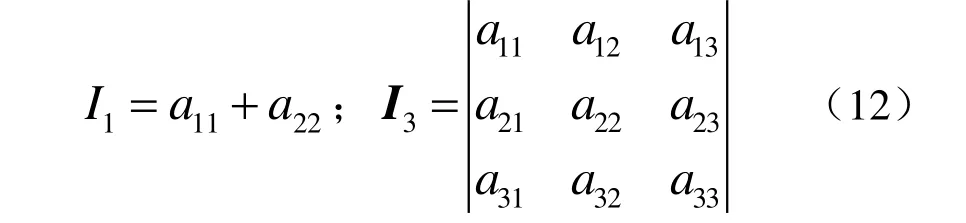
顶点坐标 ( x0, y0)

其中

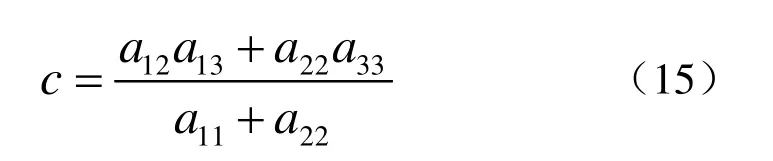
通过以上方法得到曲线的参数表达式以后，也就得到了曲线的类型以及相应的几何参数，将曲线类型和其对应参数建立数据链表以备后续的对称检验算法使用。

3 斜对称轴检测

Kanade[13]最早给出了斜对称的定义：斜对称是实际的对称性在投影到图象平面时产生的，即在2D 图形中反映的3D 世界中的真实对称。斜对称的3 个基本参数为对称轴方向角、横断线方相角以及对称轴位置。

平面内的斜对称轴检测情况一共分为4 种：① 一条曲线；② 一对曲线；③ 一对直线和一条直线；④ 两对直线。针对第①、③、④种情况已有较成熟的算法，在此不再累述，本文提出的改进算法是针对第②种情况，Sugimoto 的算法只给出了曲线是椭圆的情况，在这里给出其他二次曲线的检测方法。

3.1 抛物线以及双曲线的斜对称轴检测

对称轴的位置大体分为两种情况：一种是位于两抛物线中间，一种是贯穿两抛物线。对于第一种情况，检测算法为：

（1） 连接两抛物线的焦点1P 和2P ，并取线段1P2P 的中点 0M ，线段1P2P 即为候选横断线；

（2） 在抛物线1 上取一系列点ia ，过ia 做线段1P2P 的平行线同抛物线2 交于点ib ，取线段iaib 的中点 iM ，拟合点 iM （i=0,1,2,…）即得到斜对称轴syL 。如图3 所示。

图3 对称轴位于两曲线中间

对于第二种情况，检测算法为：

这种情况下只有一种对称的可能即对称轴为两抛物线焦点的连线。因此，只需连接两焦点即可得到斜对称轴。如图4 所示。

图4 对称轴穿过两曲线

4 斜对称面的构造

4.1 寻找对称面多边形的边

如果在一个实体的平面投影中存在斜对称，那么一定可以找到一个或多个斜对称平面，且这些斜对称平面一定同实体的边界或顶点相交，即斜对称平面在实体内为一个多边形（见图5）。因此，如果找到该对称平面同实体的所有交线，就找到了该多边形的所有边，从而就得到了斜对称平面。Zou[8]的算法是针对平面体的，因此得到的交点要么是实体的顶点，要么是对应边的中点，并且对称多边形的边均为直线段，本文将实体范围扩展到了二次曲面体，因此斜对称面也就相应地扩展到了曲边多边形。

图5 实体中的斜对称面

考虑到对称面多边形的边要么是某平面的对称轴，要么是实体的一条真实边。故把所有检测到的对称轴连同实体的边组成Axes 表，作为对称面多边形的边的候选。同时建立VertexPairs表、CurvePairs 表以及FacePairs 表分别存放对应于对称轴Axes 对称的点对、曲线边对（也包括直线边）以及面域对。

如图6 所示，从Axes 表中取出一条边 iaxes ,假定其中一对对称边为1l 和1l′，1f 和1f′则是分别同它们相邻的面域，如果1f 和1f′中所有的边界曲线均关于轴 iaxes 对称，那么面域1f 同1f′关于轴 iaxes 对称，相应地把1f 和1f′中所有的边放入 CurvePairs 表中，所有的顶点放入VertexPairs 表 中，把1f 和1f′放入FacePairs 表中，接着选取下一组对称边，重复上述过程，如图中的曲线对2l和，检测到与它们相邻的斜对称面域为 f2和，依次类推，当同CurvePairs 表中的所有元 素相邻的面域均能在FacePairs 表中找到时，表明满足斜对称关系，即该对称轴位于对称面多边形内。下面是一些性质定理，用于算法中错误情况的判定，能够有效地提高算法效率。

图6 对称的点、线、面对

性质定理1 某一实体关于一平面呈斜对称时，该实体的所有表面均应出现在FacePairs 表中，否则说明该实体无斜对称性。

性质定理2 如果在FacePairs 表中出现了两个相同的面域，则该面域中一定包含着对称平面多边形的一条边。

性质定理3 在FacePairs 表中的两个面域相交于一条边，那么该边一定是对称平面多边形的一条边。

算法具体步骤如下：

（1） 把检测到的所有面的对称轴以及实体的边界曲线放入Axes 表中；

（2） 选取Axes 表中的一个对称轴，同时置VertexPairs 表、CurvePairs 表以及FacePairs表为空；

（3） 把找到的关于该对称轴的曲线对放入CurvePairs 表中；

（4） 按以下三步进行：

1） 从CurvePairs 表中选择一个新的曲线边对，当CurvePairs 表中所有曲线边对均被处理完时，转入步骤（5）；

2） 对于选中的曲线边对，检测其所有相邻的面域，满足对称关系的面域对放入FacePairs表中，相应的边和顶点存入CurvePairs 表和VertexPairs 表中；

3） 如果没有任何相邻面域满足对称关系，则该轴不位于对称面多边形内，同时转入步骤（5）；

（5） 如果所有同该轴相邻的面域均能在FacePairs 表中找到时，说明该轴位于对称面多边形内，并将其存入对称多边形边表中，否则删除该轴，并转入步骤（2）。

4.2 构造对称面

上一步中找到的所有的位于对称面多边形内部的对称轴中既包含了对称面多边形的边，同时还有位于多边形面内的对称轴，而构造对称面多边形只需用到边界上的直线和曲线，因此需要将位于面内的直线和曲线去除。方法是利用边界曲线同内部曲线的拓扑性质入手：边界曲线的交点一定位于实体的边或者面上；而内部曲线的交点一定位于实体的内部。具体判定准则如下：

（1） 边为直线情况

1） 如果两直线的交点坐标满足实体边或表面的方程，并且两直线上的任意一内点满足实体的表面方程，那么这两条直线均为对称面的边，同时保留。

2） 如果两直线的交点坐标满足实体边或表面的方程，并且其中一条直线的内点满足实体的表面方程，那么该直线是对称面的边，予以保留，另外一条内点不满足实体表面方程的直线则被去除。

3） 如果两条直线的交点不满足实体边或表面的方程，即两条直线均为内部直线，同时被去除。

（2） 边中含有曲线的情况

1） 由于作为对称面边界的曲线一定是位于二次曲线面体的曲面部分，故其某一曲线的任意内点坐标均应满足曲面的参数方程，否则一定不是边界曲线，去除之。

2） 同被检测出的边界曲线相交的直线，其直线的任意内点坐标一定要满足实体的表面方程，否则被除去。

运用极左邻边搜索法[10]提取生成对称面的方程，加上各个实体表面的方程约束便得到斜对称多边形的方程。

5 结果及讨论

图7 中所示的红线为边界的平面为使用本算法检测到的斜对称面，由于算法对于实体的摆放位置没有要求，因而可以识别轴线任意放置的二次曲面体。

对称面的检测对于三维重建有着十分重要的意义，利用检测到的二次曲面体的对称面可以去除多余约束，方便地实现二次曲面实体的三维重建。

图7 二次曲面体及其检测到的斜对称面

[1] LIPSON H, SHPITALNI M. Optimization-based reconstruction of a 3D object from a single freehand line drawing [J]. Computer Aided Design, 1996, 28(8): 651-663.

[2] OH W G, ASADA M, TSUJI S. Model-based matching using skewed symmetry information [C]// Proc. Int'l Conf. Pattern Recognition, 1998: 1043-1045.

[3] YIP R HOUGH. A transform technique for the detection of reflectional symmetry and skew-symmetry [J]. Pattern Recognition Letters, 2000, 21: 117-130.

[4] SHEN D G, IP H H S, TEOH E K. Robust detection of skewed symmetries by combining local and semi-local affine invariants [J]. Pattern Recognition, 2001, 34: 1417-1428.

[5] YIP R K K, TAM P K S, LEUNG D N K. Application of elliptic Fourier Descriptors to symmetry detection under parallel projection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(3): 277-286.

[6] ZABRODSKY H. Computational aspects of pattern characterization-continuous symmetry [D]. Hebrew University, Jerusalem, Israel, 1993.

[7] SUGIMOTO K, TOMITA F. Detection of skewed-symmetrical shape [C]//Proceedings of the International Conference on Image Processing. Austin, Texas, USA, 1994: 696-700.

[8] Zou H L, Lee Y T. Skewed mirror symmetry detection from a 2D sketch of a 3D model [C]//Proceedings of the 3rd International Conference on Computer Graphics and Interactive Techniques in Australasia and South East Asia, 2005: 69-76.

[9] Zhang Aijun, Zhu Changqian, Xue Yong. Reconstruction of curvilinear 3D objects from orthographic views [J]. Journal of Computer Research and Development (in Chinese), 2002, 39 (11): 1423-1428.

[10] Kuo M H. Reconstruction of quadric surface solids from three-view engineering drawings [J]. Computer-Aided Design, 1998, 30(7): 517-527.

[11] Sugimoto K, Tomita F. Boundry segmentation by detection of corner, inflection, md transition points [C]// Proc. IEEE Workshop on Visualization and Machine Vision, 1994: 13-17.

[12] Lequette R. Automatic construction of curvilinear solid from wire-frame views [J]. Computer-Aided Design, 1988, 20(4): 171-180.

[13] KANADE T. Recovery of the three-dimensional shape of an object from a single view [J]. Artificial Intelligence, 1981, 17: 409-460.