二次函数中的数学思想

易小聪

数学思想是数学解题的“灵魂”，总结概括数学思想有利于透彻地理解所学知识，提高独立分析问题和解决问题的能力。二次函数中隐含着许多重要的数学思想，需要我们去挖掘和运用。归纳起来主要有以下几种。

一、数形结合思想

数形结合思想就是把数、式与图形结合起来考虑，用几何图形直观地反映和描述数量关系，用代数方法来分析几何图形中蕴含的数量关系，从而使问题巧妙快速解决。解决这类题，首先，要注意学会观察，提高图形信息的识别能力，其次，要学会分析和推理，作出正确的判断。

例1，下图都是而此函数y=ax2+bx+a2-1 的图像，若b>0 ，则a 的值等于 （ D ）

解析：∵b>0，而抛物线（a）（b）中b<0

∴抛物线不可能是（a）（b），

又∵（c）（d）中对称轴x=-■<0

∴只有（c）f符合

又∵a2-1=0

∴a=1或a=-1（舍去）

∴a的值只能为1，选D

二、函数方程思想

函数方程思想是将数学问题转化为方程（组），通过解方程（组）或运用方程的性质来分析，转化问题，使问题得以解决，函数与方程思想是密切相关的。

例2：已知抛物线y=x2 +（2k+1）x-k2+k

（1）求证：此抛物线与X轴有两个不同的交点。

（2）当k=0 时，求此抛物线与坐标轴的交点坐标。

解析：（1）与X轴有两个不同的交点，证明方程 ×2+（2k+1）x-k2+k=0有两个不相等的实数根即可。

（2）通过解方程，求值即可。

解：（1）∵b2-4ac=（2k+1）2-4x（-k2+k）=8k2+1>0

∴方程x2+（2k+1）x-k2+k=0有两个不相等的实数根。

∴抛物线与 X轴有两个不同的交点。

（2）当k=0 时，原抛物线为y=x2+x

由x=0 得y=02+0=0

x2+x=0得x1=0，x2=-1

∴此抛物线与 y轴的交点坐标为（0，0），与 X轴的交点坐标为（0，0），（-1，0）。

三、整体思想

整体思想就是根据问题的整体结构特征，把一组数或一个代数式或几个图形视为一个整体，去观察、分析、探究问题的一种方法，从而使问题得以简捷巧妙的解决。

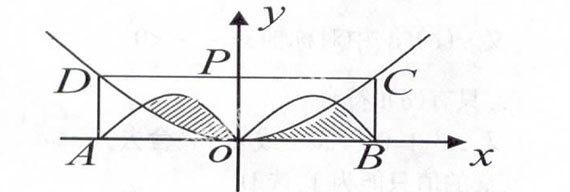
例3：如图，矩形ABCD 的长AB=4cm ，宽AD=2cm , op⊥AB是 的中点， ,两半圆的直径分别为OA 与OB ，抛物线的顶点是O ，关于OP 对称且经过 C、D 两点，求图中阴影部分面积？

解析：由抛物线顶点是O ，关于 OP对称且经过 C、 D两点，根据抛物线、矩形的对称性可知，S阴=S半圆

∴s=s=1/2π g=π/2 （cm）

注：解此题的关键是运用对称性，把两个不规则的阴影部分视为一个整体。

四、分类讨论思想

所谓分类讨论思想，就是将要研究的数学对象按照一定的标准划分为若干类不同的情形，然后再逐步进行研究和求解的一种数学解题思想。对于因存在一些不确定因素，解答无法用统一的方法或者结论不能以统一表述的数学问题，我们往往将问题划分为若干类来解决。

例4：抛物线 y=x2+2x+k与x轴交点的个数为（）

A.0个

B.1个

C.2个

D.不能确定

解析：求抛物线与 X轴交点的个数由△ 决定 b2-4ac=4-4k， k为未知数，需讨论

① k=1时，4-4k=0 ，抛物线与x 轴有一个交点

② k>1时，4-4k>0，抛物线与x 轴有两个交点

③ k>1时，4-4k<0 ，抛物线与 x轴无交点

∴应选择D

五、转化思想

转化思想是解决数学问题的一种重要思想，在解题过程中，我们往往不是对问题进行正面的直接的攻破，而是把问题进行变形、转化，把复杂的、生疏的问题转化为简洁的、熟悉的，或已经解决了的，或容易解决的问题，从而使问题得到解决，这就是转化思想。

现实生活中的“拱桥类”问题通常转化为二次函数来解决。

例5：已知一条双向公路隧道，其横断面由抛物线和矩形ABCD的三边组成，隧道最大高度为4.9米，AB=10米，BC=2.4米，有一辆高为4米，宽为2米，装有集装箱的汽车通过隧道，问：如果不考虑其它因素，汽车的右侧离开隧道石壁多少米才不至于碰到隧道顶部？

解析：建立恰当的平面直角坐标系可求解。

解：以CD所在直线为 轴，CD中点为原点，建立直角坐标系，则抛物线顶点P在 轴上，所以P（0，2.5），C（5，0），D（-5，0）

设抛物线为y=ax2+k,k即抛物线与y轴交点纵坐标，

∴k=2.5

∴a（5）2+2.5=0

a=-1/10

∴y=-1/10x2+2.5

当汽车高为4米时，在抛物线隧道中对应是纵坐标为 =4-2.4=1.6

∴1．6=- 1/10x2+2.5

解得 x=±3

故汽车要通过隧道，右侧至少要离开隧道石壁3米才不至于碰到隧道顶部。

从以上各题可看出，二次函数中，数学思想无处不在，这就要求我们在知识传播过程中适时加以渗透，将有助于学生领会和把握新知识，有助于提高解题能力，有助于培养和发展思维能力。