“图形分离法”在农村初中数学教学中的应用举例

王礼胜

农村初中数学教学手段相对落后，学生数学学习基础比较薄弱，空间观念尤其欠缺，“喜数(往往仅限于算术计算)厌形”是农村初中学生中比较普遍的现象。怎样让他们克服辨析图形的困难，掌握图形的性质，建立学习图形知识的信心，发展他们的空间观念，是农村初中数学教师必须解决的问题。“教无定法，贵在得法”，要在初中数学教学中取得好的效果方法很多，在这里仅就笔者的教学实践谈谈“图形分离法”。

面对一个比较复杂的图形时，在保持图形中各元素(点、线、角等)相对位置不变的情况下，提取出原图的一部分进行分析，从而解决问题的方法就是图形分离法。分离图形既是一种有效的解题方法，也是学生空间观念的重要组成部分。在图形教学中适当地运用“分离图形”的方法会收到事半功倍的效果，从这个意义上说，图形分离法也是一种教学方法。

一、分离基本图形，帮助学生把握基本图形的特征。掌握几何基本概念

能否灵活地运用“图形分离法”解题，首要前提就是看学生是否掌握基本概念，是否准确把握基本图形的特征。

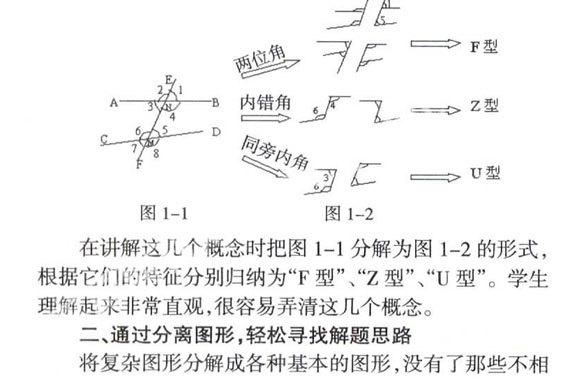
例如，要解决关于平行线的相关问题，必须先牢固掌握“三线八角”这种几何模型(即两条直线被第三条直线所截)的特征，能准确地识别同位角、内错角、同旁内角。这是新人教版七年级数学第5.1.3节的教学内容，对这一知识掌握得好与坏将直接影响到后续知识的学习，在这里运用“图形分离法”可以收到理想的教学效果。

如图1-1，直线EF分别与AB、cD相交，形成了8个小于平角的角，在这里主要探讨没有公共顶点的两个角的位置关系。如∠1与∠5，在两条被截直线AB、CD的同一方，在截线EF的同一侧的两个角，叫做同位角；如∠4与∠6，在两条被截直线AB、CD之间，分别在截线EF的两侧的两个角，叫做内错角；如∠3与∠6，在两条被截直线AB、CD之间，在截线EF的同一侧的两个角，叫做同旁内角。

在初中数学图形内容的教学中，运用“图形分离法”提高教学效果的例子不胜枚举。但应该注意到“图形分离法”的运用要适度，要有明确的目的，有时结合“图形的组合”进行训练效果会更好。

总之，针对农村初中学生比较害怕几何的情况，根据图形教学内容和学生学习情况精心设计运用“图形分离法”，可以帮助学生掌握几何基本概念，增强他们对图形的认知力，提高他们分析、解决图形问题的能力。这样就能逐步消除学生对几何学习的恐惧感，使学生建立起学习图形知识的信心，产生学习几何的兴趣，主动地去探索图形的奥秘，从而有效地促进学生空间观念的发展。