模糊自动机的强连通性及群自动机
柏明强,莫智文
(四川师范大学数学与软件科学学院,四川成都 610068)
模糊自动机的强连通性及群自动机
柏明强,莫智文
(四川师范大学数学与软件科学学院,四川成都 610068)
为了更好地研究模糊自动机的结构和性质,采用代数的方法,在传统的模糊有限状态自动机的基础上,通过定义状态集合为代数群的自动机,讨论了这一类自动机的连通性和正则性,这丰富了模糊自动机理论.
模糊自动机;群;强连通
1 前言
自动机理论是经典语言理论的一个重要内容,虽然其理论较为完善,但是研究成果仍然不断涌现[12].自1965年Zadeh[3]提出了模糊集合的概念后,Wee[4]迅速将模糊集应用于自动机理论的研究,提出了模糊自动机.到现在为止,模糊自动机与模糊语言的研究成果也是十分丰富[59].强连通自动机是在自动机中的一种十分特殊的自动机,其不同于文[1-9]中的自动机,它要求状态转移必须是任意状态之间均可进行.群自动机[1013]是在经典自动机基础上扩展而成的.其将一般的状态集拓展到代数群上.本文将群自动机和模糊集理论结合,提出了模糊群自动机的概念,这是模糊自动机理论的自然推广.
设Σ是字母表,Σ∗是Σ上的字符串集合,是一个么半群.设x=a1a2…an是一个字符串, 称an…a2a1为x的逆像,记为xR.ε为空字符.
2 强连通模糊自动机
定义2.1[6]一个模糊有限自动机是一个五元组A=(Q,Σ,δ,I,F),其中Q是状态的非空有限集,Σ是非空有限字母表,δ:Q×Σ→Q×[0,1]为状态转移函数,I⊆Q是初始状态,F⊆Q是终止状态集.
为了运算的方便,定义映射δ0为δ0(q,x)=p,当且仅当δ(q,x)=(p,µ),从而状态转移函数δ∗可以扩展为从Q×Σ∗到Q×[0,1]的映射,满足:(1)∀q∈Q,δ∗(q,ε)=(q,1);(2)∀q∈Q,x∈Σ,y∈Σ∗,δ∗(q,xy)=δ∗(δ∗(q,x),y),其中δ(q,xy)=(p,µ),δ(q,x)=(p1,µ1),δ(p1,y)= (p,µ2),µ=min{µ1,µ2}.
定义2.2设A=(Q,Σ,δ,I,F)是模糊有限自动机.如果∀q,p∈Q,均存在x∈Σ∗,使得δ(q,x)=(p,µ)且δ(p,xR)=(q,µ0),则称A是模糊强连通自动机.
对于强连通自动机来说,其状态转移图是连通图,而且是完全图.
定义2.3设A1=(Q1,Σ,δ1,I1,F1)和A2=(Q2,Σ,δ2,I2,F2)是模糊有限自动机,ϕ是从Q1到Q2的映射.

(2)如果ϕ是从Q1到Q2的同态映射,且ϕ是双射,则称ϕ是从A1到A2的同构映射.
(3)如果A1和A2之间存在同构映射,则称A1与A2相互同构,记为A1~=A2.
如果A1=A2,则称A1与A2之间的同态和同构分别称为自同态和自同构.记E(A)和G(A)分别为A上所有自同态和自同构构成的集合.显然E(A)和G(A)分别为么半群和群.
性质2.1设A=(Q,Σ,δ,I,F)是一个强连通自动机.如果ϕ,ζ∈G(A),且存在q0∈Q使得ϕ(q0)=ζ(q0),则∀q∈Q,均有ϕ(q)=ζ(q).即如果ϕ,ζ只要在某点的像相同,则ϕ=ζ.
证明由于A是强连通的,∀q∈Q,必存在x∈Σ∗,使得δ(q0,x)=(q,µ),从而δ0(q0,x)=q,所以ϕ(q)=ϕ(δ0(q0,x))=δ0(ϕ(q0),x)=δ0(ζ(q0),x)=ζ(δ0(q0,x))=ζ(q).
性质2.2设A=(Q,Σ,δ,I,F)是一个强连通自动机.则|G(A)|整除|Q|.
证明∀p,q∈Q,如果存在ϕ∈G(A),使得ϕ(q)=p,则记p~q.显然“~”是Q上的一个同余关系.记[q]={ϕ(q)|ϕ∈G(A)}.显然[q]是含q且与q同余的一个类,称为同余类.

定义2.4[9]设A=(Q,Σ,δ,I,F)是模糊有限自动机.如果∀q∈Q,∀x,y∈Σ∗,均有δ(q,xy)= δ(q,yx),则称A是可交换的.
交换性是代数中的一个重要性质,在自动机理论有很重要的地位.
如果一个交换的模糊有限自动机是强连通的,则称其是完美自动机.
定理2.1设A=(Q,Σ,δ,I,F)是一个模糊有限自动机,则A是完美的充分必要条件是A是强连通的,|G(A)|=|Q|,且G(A)是可交换的.

从而ϕζ=ζϕ,即G(A)是可交换的.
4)由于A是完美的,所以A必是强连通的.
(充分性)欲证A是完美的,根据条件知,只需要证明A是可交换的即可.
∀q∈Q,x∈Σ∗,由ϕx(q)=δ0(q,x)定义的映射ϕx必是A上的自同构映射.


3 群矩阵型模糊自动机
定义3.1[13]设G是一个有限群.设G0=G∪{0},其上定义了两个代数运算乘法“·”和加法“+”:


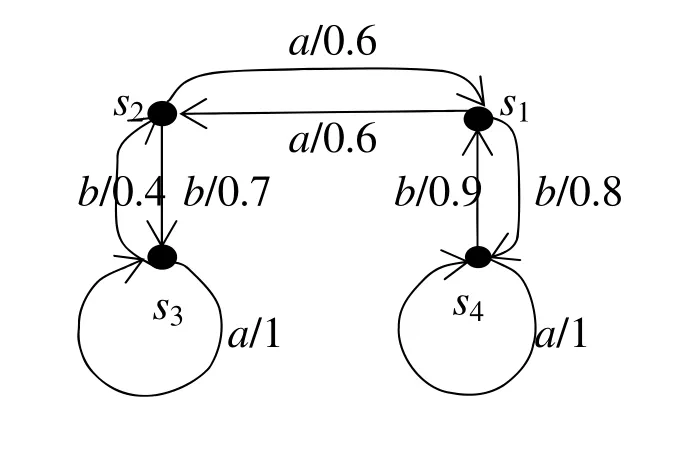
图3 .1 A的状态转移图


4 结论
自动机的强连通性是自动机理论中的一个重要研究内容.其良好的状态转移导致了研究工具的多样化.在本文,将模糊自动机理论中的状态集推广到一般的代数群中.利用自动机的连通性和代数群理论,讨论了群自动机的正则性.
[1]Hopcroft J E,Ullman J D.Introduction to Automata Theory,Languages and Computation[M].New York: Addison-Wesley,1979.
[2]Eilenberg S.Automata,Languages and Machines[M].Burlington:Academic Press,1976.
[3]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8:338-353.
[4]Wee W G.On generalizations of adaptive algorithm and application of the fuzzy sets concept to pattern classification[D].West Lafayette:Purdue University,June 1967.
[5]柏明强.模糊正则表达式与模糊有限态自动机的关系[J].纯粹数学与应用数学,2000,16(4):1-6.
[6]Su Lan,Mo Zhiwen.Closure of the fuzzy finite state languages[J].Fuzzy Sets and Systems,1995,75:393-397.
[7]Lee E T,Zadeh L A.Note on fuzzy languages[J].Information Science,1969,1:421-434.
[8]Zoltan Esik,Guangwu Liu.Fuzzy tree automata[J].Fuzzy Sets and Systems,2007(1):1450-1460.
[9]柏明强.Fuzzy交换正则语言注记[J].四川师范大学学报:自然科学版,2005,28(4):391-393.
[10]Ito M.A representation of strongly connected automata and its applications[J].J.Comput System Sci., 1978,17:65-80.
[11]Sengupta A.On a group-matrix type automaton with output[J].Acta Math.Hung.1986,48(3-4):347-352.
[12]Barnes B I-I.Groups of automorphisms and sets of equivalence classes of input for automata[J].J.ACM, 1965,12:561-565.
[13]Feichtinger G.Some results on the relation between automata and their automorphism groups[J].Computing, 1966,1:327-340.
Connectedness of fuzzy automata and group automata
BAI Ming-qiang,MO Zhi-wen
(Colledge of Mathematics and Software Science,Sichuan Normal University,Chengdu610068,China)
In order to study the structure and properties of fuzzy automata,based on theory of general fuzzy finite state automata,a kind of fuzzy automata is introduced with its states set made up of algebra group matrix by algebra methods.The connectedness of fuzzy automata is discussed,then the regularity too.This is a foundation for further researches on fuzzy automata.
fuzzy automata,group,strongly connected
O235
A
1008-5513(2009)03-0454-05
2008-11-10.
国家自然科学基金(10671030),四川省青年科技基金项目(07ZQ026-114).
柏明强(1976-),讲师,主要研究方向:形式语言与自动机.
2000MSC:03D12,68Q68

