关于勒让德多项式与契贝谢夫多项式间的关系
杨倩丽,刘欣宇
(渭南师范学院数学与信息科学系,陕西渭南 714000)
关于勒让德多项式与契贝谢夫多项式间的关系
杨倩丽,刘欣宇
(渭南师范学院数学与信息科学系,陕西渭南 714000)
主要研究勒让德多项式与契贝谢夫多项式之间的关系的性质,利用生成函数和函数级数展开的方法,得出了勒让德多项式与契贝谢夫多项式之间的一个重要关系,这对勒让德多项式与契贝谢夫多项式的研究有一定的推动作用.
勒让德多项式;恒等式;契贝谢夫多项式
1 引言及主要结论

的系数定义的,它们在函数的正交性理论研究中占有十分重要的位置,并引起了不少学者的重视和兴趣,文[1-4]利用此理论给出了Fibonacci数的一些性质.本文得到勒让德多项式与契贝谢夫多项式之间的一个重要关系.
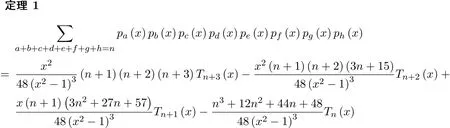
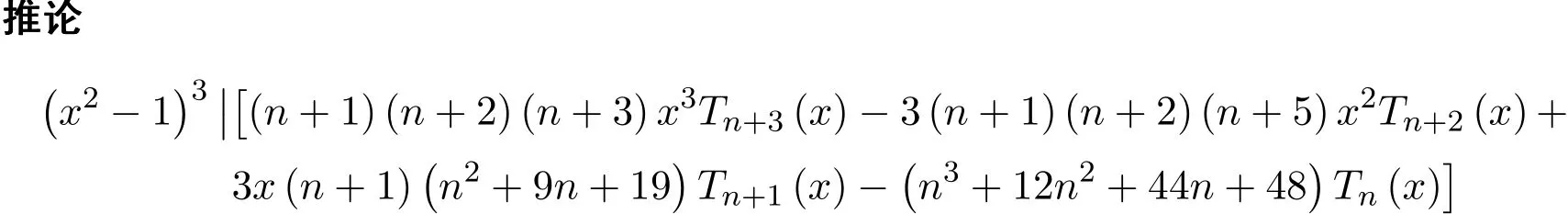
2 几个引理


3 定理的证明
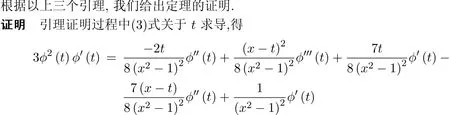



于是完成了定理的证明.
[1]Zhang Wenpeng.Some identities involving the Fibonacci numbers[J].The Fibonacci Quarterly,1997,35:225-229.
[2]Li Hailong.On generalized Euler constants and an integral related to the Piltz divisor problem[J].Proc.Sci. Sem.Fac.Phys.Math.Siauliai Univ.,2005,8:81-89.
[3]Li Hailong,Toda M.Elaboration of some results of Srivastava and Choi[J].Journal of Analysis and Application,2006,25:517-533.
[4]Li Hailong,Kanemitus S.Tsukada H.Modular relation interpretation of the series involving the Riemann zeta values[J].Proceedings of The Japan Academy Series A:Mathematical Sciences,2008,84(8):133-162.
[5]周亚兰,王霞.勒让德多项式的性质与契贝谢夫多项式间的关系[J].纯粹数学与应用数学,1999,15(4):75-81.
On relationship of Legendre polynomials and Chebyshev polynomials
YANG Qian-li,LIU Xin-yu
(Department of Mathematics and Information Science, Weinan Teachers University,Weinan714000,China)
This paper discusses a property of the Legendre polynomials and Chebyshev polynomials,by a means of form faction and function series,an important relationship of the Legendre polynomials and Chebyshev polynomials is given.It will have a certain impetus to the research of the Legendre polynomials and Chebyshev polynomials.
Legendre polynomials,identity,Chebyshev polynomials
O156.4
A
1008-5513(2009)03-0448-06
2007-11-10.
陕西省自然科学基金(SJ08A22).
杨倩丽(1964-),教授,研究方向:数论.
2000MSC:11B83
——庆祝湖南农业大学草业科学系建系20 周年

