为迁移而教 为思维而学
朱志明 胡小林
笔者认为,“为迁移而教,为思维而学”是永远不会过时的话题。因为它既符合学生的认知规律,又符合时代的发展要求。根据这一思想,2008年11月笔者设计了“四边形分类”[北师大版《数学》四年级(下册)第32页]教案,并由胡老师执教,收获颇丰,荣获了衢州市小学数学优质课评比一等奖。现再次回放,与同行们商榷。
[课堂实录]
一、课前谈话,孕育新知
师:现在我们教室里有这么多人,你能分分类吗?(生答略)
师:你是按什么标准分的?(生答略)
二、出示课题,了解起点
师:今天我们学习“四边形的分类”。关于这个话题你想说什么?
生1:什么是四边形?
生2:可分几类?
师:谁能解决第一个问题?
生3:由四条线段围成的图形叫四边形。
师:谁能解决第二个问题?
生4:好像可分为平行四边形、长方形、正方形和梯形。
师:什么是平行四边形和梯形呢?(生难以回答准确)
师:看来,同学们对四边形的分类知道了一些知识,但不够全面、准确,我们有必要继续研究它。

三、分类探究。得出新知1分一分
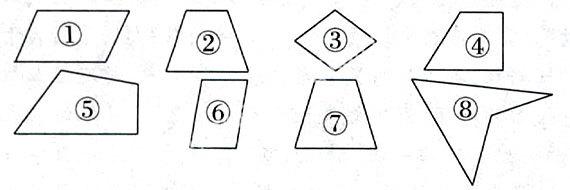
师:请同学们拿出信封里的四边形,先观察其特点,再确定一个标准,然后同桌合作分一分。生合作分类)
小组汇报,教师根据学生的分法粘贴在黑板上。
学生分法之一——按边分①③⑥一类、②④⑦一类、⑤⑧一类。
分法之二——按角分①②③⑥⑦⑧一类、④⑤一类。
师:分法之二,是按什么标准分的。(生答略)
师:我们今天主要研究按边分。谁能说说分法一的分类标准和每一类的特点?
生:分类标准是有多少组对边平行。①③⑥这一类有两组对边平行,②④⑦这一类只有一组对边平行,⑤⑧这一类没有一组对边平行。
2下定义
(1)为平行四边形、梯形下定义
师:有两组对边分别平行的四边形称为什么四边形呢?只有一组对边平行的四边形称为什么四边形呢?(生答略)
(2)初步运用概念
师:刚才同学们给四边形家族的成员分了类,表现都不错,淘气在图形王国游玩时碰到了一个难题——长方形和正方形应属哪一类四边形呢?谁能帮忙解决?
(学生独立思考后讨论汇报)
生2:长方形和正方形应属平行四边形。
生2:长方形和正方形应单独分类。
师:请各自说说理由。
生1:长方形和正方形也有两组对边平行,有两组对边平行的四边形是平行四边形。
生2:长方形和正方形的角都是直角,其他平行四边形的角不是直角。
生3:平行四边形、梯形是按边分产生的,它与角无关。只要满足有两组对边平行的条件,就应规定为平行四边形。
师(面对生2):现在你赞成长方形和正方形是平行四边形的结论吗?(生2点头)
师:长方形与正方形是平行四边形,但它的角都是直角,我们把它称为——特殊的平行四边形(生说)。
师:梯形按角分,可分为几类呢?
生:直角梯形和不是直角梯形。
(3)给出梯形上、下底和腰的名称
板书:(略)
四、边学边练。巩固新知
1填一填
师:刚才同学们认识了平行四边形和梯形,现在请同学们运用这一知识完成作业纸上的“填一填”(见教材第32页)。
(汇报略)
2画一画
在点子图上按要求画图。
(1)学生画与汇报
师:请你说说画的方法。
生1:画平行四边形时。我先在第一行上画三格的线段,再在第四行上画三格的线段,连接起来就是平行四边形。
师:老师有一个疑问,你为什么耍在行的点子上画线段?
生1:这样画,这一组对边肯定平行。
师:其他同学有没有疑问?
生2:这一组平行线段,你为什么都要画三格?
生1:这样画保证了另一组对边平行?
(梯形与三角形的画法汇报略)
师:通过画图,你发现了什么。
生3:画平行四边形的方法:上下对边既要画平行,又要画相等。
生4:画梯形的方法:上下这一组对边画平行,但不能画相等。
(2)变式画图
师:老师把一组平行的对边竖着画,你们认为能画出平行四边形吗?
师:通过刚才画图,你发现了什么?
生1:平行四边形和梯形的形状有许多,画时可以正画,也可以斜画。
生2:平行四边形、梯形和三角形可以互变。
师:谁能说具体一点?
生3:当梯形的上下两底相等时,就变成了平行四边形;当一底为零时,就变成了三角形。
3添一添
按下面的要求添线段。
(1)在一个三角形中,添上一条线段,使它变成一个梯形和一个三角形。
(2)在下面的平行四边中,添上一条线段,使它变成两个一模一样的图形。
学生独立操作后汇报(第一小题的汇报略)。
师:第二小题许多同学完成了四种添线段的方法。谁来说说你是怎样添的?
生1:我添了一条对角线,把平行四边形分成了两个一模一样的三角形。
生2:我添了一条上下对边取中点的线段,把平行四边形分成了两个一模一样的平行四边形。
师:通过刚才的画图与汇报,你发现了什么?
生:两个一模一样的三角形可以拼成一个平行四边形……
五、引导反思。深化新知
师:请同学们回顾一下,通过这节课的学习你有什么收获?或者还有什么疑问?
师:如果用一个圆圈表示所有的四边形,这个圆圈应分几块,每块表示什么四边形7表示长方形、正方形的圈又应画在哪里?
(师生完成集合图)
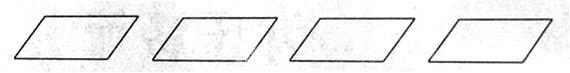
[总评析]
本实录的主要特点有以下两点:
一、为迁移而教
上述设计主要在以下环节体现了为迁移而教:①课前谈话,给教室里的人分类,为“四边形分类”围绕分类要点(需要一个标准,每个对象既不能重复。也不能遗漏)研究作迁移;②平行四边形和梯形的概念学习为长方形、正方形的对号入座作迁移;③点子图上画图的方法为“添一添”环节的学习作迁移;④画图或添线段的环节中,让学生归纳画图的方法和发现规律,为五年级学习平面图形的面积作迁移。
二、为思维而学
本设计关注了学生三方面思维的培养:其一是思维的概括性。“思维的概括性是指善于把分散的、个别的问题进行概括,得出一般性的结论,以指导实践活动”。其二是思维的深刻性。“思维的深刻性,是指善于钻研问题。善于从纷繁复杂的表面现象中,发现最本质最核心的问题,而不被表面现象所迷惑”。具体体现在“画一画”与“添一添”的教学环节,教者不是把教学停留在学生画的结果的是非判断上,而是让学生总结画的方法。概括发现规律。其三是思维的广阔性。“思维的广阔性表现在善于全面地分析研究问题。着眼于事物之间的联系和关系,找出问题的本质,并能在许多不同知识和实践的领域内进行创造性思考。”

