暴雨强度的总公式与分公式的精度比较

陈鹏飞　樊建军　王晓峰　林　林

摘要：文章采用规范规定的多个样法进行雨样选取处理，通过P-Ⅲ、Weibull分布模型对雨样进行频率分析优选出误差最小的理论分布推求出P-i-t表，应用遗传算法、拟牛顿算法、高斯牛顿法推求暴雨强度的总公式与分公式，并对其计算精度进行分析比较。结果表明：不管总公式还是分公式其计算精度均能满足《室外排水设计规范》的要求，但分公式的计算精度明显高于总公式。

关键词：暴雨强度；暴雨公式；精度比较

中图分类号：P333文献标识码：A文章编号：1009-2374（2009）06-0125-02

一、暴雨公式推求的步骤

城市暴雨强度公式作为城市排水设计的基础公式，其正确与否将直接关系到城市基础设施建设的科学性。推求暴雨强度公式的工作的程序按时间先后可以分为三部分：第一部分为选取雨样；第二部分为频率分析；第三部分为推求公式。

（一）选取雨样

城市暴雨资料的收集、暴雨强度资料的选样与统计方法及与之相关的频率分布线型选择是城市暴雨强度公式制定过程中的前段工作，也是极其关健的环节，因为它直接影响编制暴雨强度公式所需的P-i-t经验数据表的质量对暴雨公式的精度有相当大的影响。选样是从现有的记录中合理选择若干个数值以组成一个样本，来作为频率分析的依据，因此暴雨强度资料的选样工作极其重要，在选样过程中要充分做到每个单元具有一致性和独立性，所组成的样本具有代表性和足够的可行性，从而在此基础上认真分析研究，再选择与之适应的频率分布线。

根据《室外排水设计规范》（GB50014-2006）的规定，本文采用年多个样法选样，完整收集1953年～2006年间某市的降雨量，对每年分别挑选并读取8场最大的暴雨中每5分钟、10分钟、15分钟、20分钟、30分钟、45分钟、60分钟、90分钟、120分钟九个时段的降雨量数据进行整理，然后统一排序，从大到小取资料年数4倍的最大值作为统计的基础。

（二）频率分析

频率分布线型的选择对城市暴雨强度公式的精确制定起到保证作用。因为它直接关系到编制公式所需的重现期-暴雨强度-历时（即P-i-t）经验数据表的可靠性。本文采用矩法、拟牛顿法、适线法、极大似然法、遗传算法对P-Ⅲ分布模型，以及采用最小二乘法、遗传算法、拟牛顿法对Weibull分布模型进行拟合分析优选出误差最小的理论分布。拟合分析的结果见表1。

表1 频率分析误差比较表

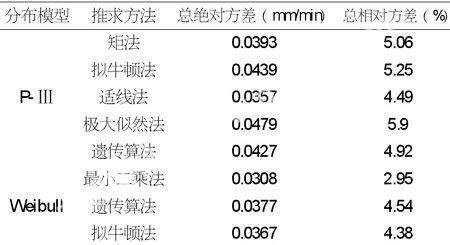
根据表1可以看出相对于Weibull最小二乘推求的P-i-t数据的误差最小，总绝对方差为0.0308，总相对方差为2.95%，均满足于规范规定的精度要求。因此将相对于Weibull最小二乘推求的P-i-t数据作为暴雨强度公式推求的基础数据。

（三）推求公式

利用以上频率分析所得的最优P-i-t数据，分别采用遗传算法、拟牛顿算法、高斯牛顿法推求暴雨强度公式。采用遗传算法、拟牛顿算法、高斯牛顿法推求暴雨强度分公式的平均绝对方差和平均相对方差见表2：

表2 分公式平均误差比较

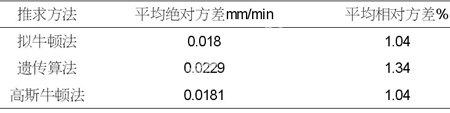
从表2中可以看出用拟牛顿法推求的暴雨强度分公式的平均误差最小。平均绝对方差为0.0180 mm/min，平均相对方差为1.04%，均满足于规范规定的精度要求。因此将用拟牛顿法推求的暴雨强度分公式的参数成果作为研究对象具体数据见表3。同理，根据表4中的参数可知，采用遗传算法推求暴雨强度总公式的误差最小。总绝对方差为0.0448 mm/min，总相对方差为3.26%，均满足于规范规定的精度要求。因此将用遗传算法推求的暴雨强度总公式的参数成果作为比较对象。

二、城市暴雨分公式和总公式精度比较

为便于对分公式计算精度进行分析，将不同重现期和历时以及表3中的参数代入各个暴雨强度分公式中即可得到暴雨强度，并与相对于Weibull最小二乘推求的P-i-t数据表中的暴雨强度进行比较[4]，分别计算平均绝对方差和平均相对方差计算其抽样误差，结果见表5。从表5结果可看出，当计算重现期在0.25~100 a之间时，无论是绝对方差还是相对方差，结果都较为理想，其中绝对方差介于0.0052~0.0453 mm/min之间，平均绝对方差为0.0180mm/min，均小于文献[2]规定的0.05mm/min；相对方差介于0.40%~2.03%之间，平均相对方差为1.04%，也小于规范规定的5% 。

同理将不同重现期和历时以及用遗传算法推求出的参数代入暴雨强度总公式中即可得到暴雨强度同样与相对于Weibull最小二乘推求的P-i-t数据表中的暴雨强度进行比较，分别计算平均绝对方差和平均相对方差计算其抽样误差，结果见表6。从表6结果可看出，当计算重现期在0.25~100 a时，绝对方差介于0.0168~0.0736 mm/min之间，平均绝对方差0.0448 mm/min虽然小于规定的0.05 mm/min，但其中0.25、0.33、0.5、50、100 a绝对方差已超过0.05mm/min；相对方差介于1.00%~7.82%之间，平均相对方差为3.26%，其中0.25、0.33、0.5a相对方差已超过5%。

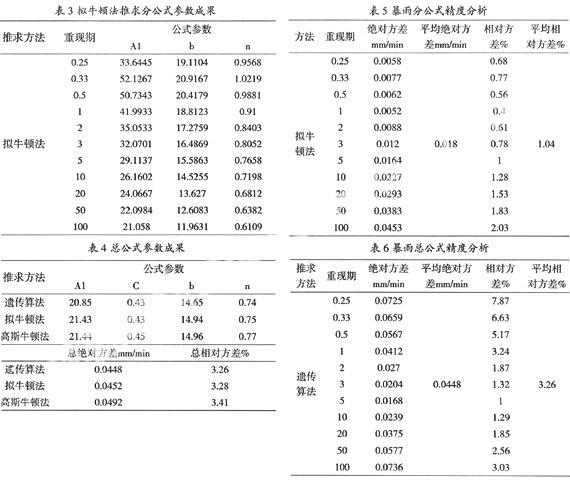
根据表5、表6及以上分析可知不论是分公式还是总公式计算的平均方差均小于现行规范规定的要求，但由分公式计算的平均绝对方差比由总公式计算的减少了0.0268 mm/min，平均相对方差减少了2.22%。并且在单一重现期时由总公式计算出的绝对方差和相对方差有部分已经超出了现行规范规定的要求，所以总的来说在进行工程设计计算过程中，当重现期为固定数值时最好使用分公式计算，因为分公式的精度明显高于总公式。

三、结论与建议

根据上述的综合分析和对比，可以得出以下结论和建议：

1．在推求暴雨强度过程中每个步骤对结果都有较大影响应采用多种方法进行分析比较从而优选。

2．不论是利用分公式还是总公式推求暴雨强度，其精度均能满足文献[2]规定的要求，但分公式的精度高于总公式，因此，在实际应用中，当确定的重现期与分公式中的一致时，应按公式计算设计暴雨强度。

参考文献

[1]张子贤．用高斯一牛顿法确定暴雨强度公式参数[J]．河海大学学报，1995，23（5）．

[2]室外排水设计规范GB50014-2006．北京：中国计划出版社，2006．

[3]夏宗尧．毒皇翩暴雨强度公式中应用P-Ⅲ曲线与指数曲线的比较[J]．中国给水排水，1990，（3）．

[4]柏绍光，黄英，方绍东，等．城市暴雨总公式与分公式精度分析[J]．人民长江，2006，37（8）．

作者简介：陈鹏飞（1986－），男，福建泉州人，广州大学硕士研究生，研究方向：建筑给水排水新技术。